Matemáticas 8º y 9º
MAURICIO MUÑOZ MATEMÁTICO FÍSICO UNIVALLE
Números Irracionales
Definición: Los números irracionales son aquellos que no pueden ser escritos en forma fraccionaria, por ejemplo: los números decimales infinitos no-periódicos, raíces no exactas y algunas constantes.
El conjunto de los números Irracionales se simboliza con la letra I.
El número irracional más conocido es 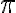 , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
Entre los números irracionales tenemos como ejemplo algunas raíces cuadradas, como por ejemplo: 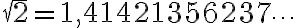 que tiene infinitos decimales de manera que no existe ninguna secuencia de ellos que se repitan.
que tiene infinitos decimales de manera que no existe ninguna secuencia de ellos que se repitan.
De donde deducimos que raíz cuadrada de 2 está entre 1 y 2. Es decir
1 < raíz de dos > 2 (raíz de dos es mayor que uno y menor a dos)
1 y 2 son valores aproximados a raíz de dos en unidades.
Si dividimos el segmento de extremos 1 y 2 en 10 partes iguales , podemos aproximar su valor a décimas como se ve en la siguiente tabla.
Números decimales | Cuadrados |
1.1 | 1.21 |
1.2 | 1.44 |
1.3 | 1.69 |
1.4 | 1.96 |
1.5 | 2.25 |
Los valores en décimas mas próximos a raiz de 2 son 1.4 y 1.5, porque sus correspondientes cuadrados están mas próximos a 2.
raiz de dos está entre 1.4 y 1.5
En matemáticas se dice : raíz de 2 mayor a 1.4 y menor a 1.5
Deducimos que 1.4 es una aproximación por defecto y 1.5 es una aproximación por exceso a raíz cuadrada de 2
Igualmente se puede hacer para centésimas, milésimas, diezmilésimas....
El video muestra una explicación de los números irracionales y otros tipos de números:
Fuente: https://www.youtube.com/watch?v=uGaFiG5x3P0
Los irracionales y la recta numérica
Localizaremos en la recta numérica, puntos correspondientes a raices cuadradas de números naturales
la extracción de la raíz cuadrada puede dar lugar a números irracionales cuando los números a los que se les extrae la raiz no son cuadrados perfectos,.
Para recordar: los números naturales como 1,4,9,16,25, son cuadrados perfectos ya que
12 = 1
22 = 4
32 = 9 y así sucesivamente.
con base en lo anterior y según las lecciones vistas, podemos afirmar que la extracción de la raíz cuadrada puede dar lugar a números irracionales cuando los números a los que se les extrae la raíz no son cuadrados perfectos.
donde n es un número natural que no es cuadrado perfecto son números irracionales
Otros números irracionales son aquellas raíces cúbicas de un númeo natural n que no es un cubo perfecto ![\sqrt[3]{2};\,\sqrt[3]{3};\,\sqrt[3]{4};\,\sqrt[3]{5};\ldots;\,\sqrt[3]{n} \sqrt[3]{2};\,\sqrt[3]{3};\,\sqrt[3]{4};\,\sqrt[3]{5};\ldots;\,\sqrt[3]{n}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/f3d3f99b82306fb3456effb925de4b7d.gif) , donde n es un número natural que no es cubo perfecto, son números irracionales.
, donde n es un número natural que no es cubo perfecto, son números irracionales.
En términos generales, si  es un número natural que no es la enésima potencia de otro número natural , entonces
es un número natural que no es la enésima potencia de otro número natural , entonces ![\sqrt[n]{a} \sqrt[n]{a}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/bf7ff33f3b129b15c06203d60f007807.gif) es un número irracional.
es un número irracional.
Por ejemplo: ![\sqrt[5]{2};\,\sqrt[6]{12};\,\sqrt[7]{25} \sqrt[5]{2};\,\sqrt[6]{12};\,\sqrt[7]{25}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/9fcf2874ca7bf81d511f141a6ece07a6.gif) , son números irracionales.
, son números irracionales.
Además, los opuestos a los números irracionales positivos también son números irracionales, como por ejemplo: ![-\sqrt{2};\, -\sqrt{5};\, -\sqrt[3]{6};\,\sqrt[3]{10} -\sqrt{2};\, -\sqrt{5};\, -\sqrt[3]{6};\,\sqrt[3]{10}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/cb4be9cf3747ed1a6e56b9a96b6ee3a9.gif) .
.
Al igual que los números racionales, a los números irracionales les corresponde un punto en la recta númerica. La manera más usual de ubicarlos es mediante construcciones geométricas.
Veamos como se puede representar 
Hay que tener claro que  ..., es decir,
..., es decir, 
Observa el cuadrado del dibujo, si ampliamos el teorema de Pitágoras para hallar su diagonal comprendemos esto:
teorema de Pitágoras:
Con la ayuda de un compás podemos representar exactamente  en la recta numérica. Sabemos que
en la recta numérica. Sabemos que  es un número irracional, por lo tanto, el punto P de la recta no puede estar ocupado por ningún otro número irracional.
es un número irracional, por lo tanto, el punto P de la recta no puede estar ocupado por ningún otro número irracional.
En el siguiente video se muestra la representación gráfica de  en la recta numérica:
en la recta numérica:
Fuente:https://www.youtube.com/watch?v=bwusbiSesL4
NOTACIÓN CIENTÍFICA
Es una herramienta para anotar números enteros o números decimales, mediante potencias de 10, esta notación es utilizada en números demasiado grandes o demasiado pequeños.
La notación científica tiene tres partes:
- Una parte entera de una sola cifra
- Las otras cifras significativas como la parte decimal
- Una potencia de base diez que da el orden de magnitud de la cifra
RECORDEMOS→
PROPIEDADES DE LA POTENCIACIÓN:
De esta definición obtenemos las siguientes propiedades, llamadas leyes de los exponentes, que nos permitirán simplificar expresiones con exponentes.
PROPIEDADES DE LA RADICACIÓN:
Los radicales podemos escribirlos como una potencia con exponente racional y les aplicamos las propiedades de los exponentes; de esta ,manera definimos las siguientes propiedades para los radicales.
Ejemplo 1:
La distancia media de la Tierra al Sol es de 149 600 000 km.
Entonces la distancia media de la Tierra al Sol se puede expresar en notación cientifica. 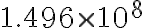
Adicionalmente, 10 elevado a una potencia entera negativa (-n) es igual a 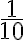
Ejemplo 2:
El diámetro de un átomo de plata es 0.00000000025 m
Notación científica en sumas y restas.
Si los sumandos son del mismo orden de magnitud sumamos o restamos los números que preceden a las potencias de 10.
Si los sumandos no son del mismo orden de magnitud se reducen al mayor de los órdenes, y se suman o se restan los números que preceden a las potencias de 10.
Notación científica en productos y cocientes
Para hallar productos y cocientes de números expresados en notación científica se aplican las reglas del producto de decimales y las propiedades de la potenciación.
Ejemplo 3:
Solución:
Cada factor lo expresamos en notación científica
Ahora efectuamos el producto:
Solución:
Escribamos cada expresión en notación científica
Ahora calculamos el cociente:
En el siguiente vídeo encuentra una explicación a fondo del tema:
Fuente del vídeo: https://www.youtube.com/watch?v=bg_4G32yCnM
PREGUNTA:
Escriba en notación cientifica el siguiente número 78563000
* 78.563*10^6 * 7.8563*10^8 * 7.8563*10^9 * 7.8563*10^7
Los números reales: igualdad y propiedades
Reconoceremos el conjunto de los números reales como la unión de los racionales e irracionales.
Los números reales: igualdad y propiedades
En la vida práctica, al realizar mediciones (en la conmensurabilidad), basta con el manejo de los números racionales y sus operaciones. Sin embargo, como vimos en la primera unidad, existen números no racionales y la inconmensurabilidad tiene solución únicamente por, la existencia de números irracionales.
Números racionales como: 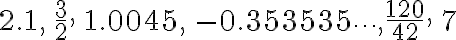 siempre tienen una expresión decimal finita (para la cual se acepta que tiene período O) o periódica de periodo diferente de O. En efecto, podemos escribir:
siempre tienen una expresión decimal finita (para la cual se acepta que tiene período O) o periódica de periodo diferente de O. En efecto, podemos escribir:
Números irracionales como:  tienen una representación decimal infinita no periódica.
tienen una representación decimal infinita no periódica.
Como estudiamos en la unidad anterior, las expresiones decimales de los números nombrados son:
1.2020020002... = 1.2020020002.
Todos los números racionales e irracionales conforman los números reales; de esa forma, un número real siempre tiene una representación decimal periódica, de período O (decimal finito) o de periodo diferente de cero, o una representación decimal no periódica
Los números racionales se representan sobre la recta, como seguramente lo has hecho. En la figura se representan los racionales: 
Sobre la recta también has representado algunos números irracionales En la siguiente figura se muestra la representación sobre la recta del irracional 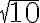
Si sobre la recta señalamos un punto, es posible determinar el número real que le corresponde teniendo como base la unidad que se ha escogido.
En conclusión, podemos decir que:
A cada número real le corresponde un punto sobre la recta y a cada punto sobre la recta le corresponde un número real. Cuando sobre la recta se representan los números reales, la recta se llama recta real.
Por otra parte, observemos los siguientes números y determinemos si son iguales o no lo son
Cuando se tienen dos números reales, de ellos se puede decir que son iguales o son diferentes. Dos números reales iguales pueden tener, sin embargo, diferente representación numérica.
son números reales iguales.
En general, se puede asegurar que si r es un número real, entonces r= r. Así:
Si r es un número real y se cumple que r = 9.5, entonces también se
cumple que 9.5 = r.
Si r y m son números reales y se cumple que r = 2.1888 Y 2.1888 = m,
entonces se concluye que r = m.
Los enunciados que hemos hecho para ciertos números reales, permiten conjeturar tres propiedades que se cumplen para Iodos los números reales y que más tarde podrás demostrar.
La igualdad entre números reales cumple las propiedades:
Reflexiva : todo número real es igual a si mismo, lo que quiere decir que si a es un número real, entonces a = a.
Simétrica: Si a, b, son números reales y a = b, entonces b = a.
Transitiva: si a, b, y c son números reales y a = b y b = c, entonces a = c.
Por cumplir estas tres propiedades se dice que la igualdad entre números reales es una relación de equivalencia
La operación logaritmación permite determinar el exponente entero al cual debe elevarse una base positiva conocida, para obtener una potencia dada. La logaritmación es la otra operación inversa de la potenciación.
El resultado de la logaritmación se indica así:

Y se lee "n es el logaritmo en base a de b". El resultado de la logaritmación tiene sentido siempre y cuando esté definida unívocamente la expresión an = b; para que ello sea posible se toman a y b positivos.
Con esa condición, se cumplen las siguientes equivalencias:
Ejemplo:
De acuerdo con las potencias, expresemos en forma de logaritmo:
PROPIEDADES BÁSICAS DE LA LOGARITMACIÓN
|1| Los números negativos no tienen logaritmo. Es una especie de convenio ya que aparecerian opuestos de los positivos y algunos negativos no tendrian logaritmo como 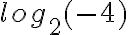 , donde
, donde 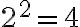 y
y  según propiedades de la potenciación.
según propiedades de la potenciación.
|2| El logaritmo de su base es 1. Así  ya que
ya que  .
.
|3| El logaritmo de 1 es cero. Así  ya que
ya que  .
.
Como las calculadoras sólo traen dos posibilidades para calcular logaritmos: log (logaritmo en base 10) y ln (logaritmo natural), se debe trasformar la base 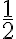 a base 10 o a base e; para hacerlo utilizamos la propiedad de los logaritmos que dice
a base 10 o a base e; para hacerlo utilizamos la propiedad de los logaritmos que dice
Así los valores para la variable independiente se calculan con
Video de explicación, para profundizar:
Fuente:
PREGUNTA: ¿Calcular el logaritmo de 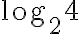 es?
es?
Expresiones algebraicas
Juan Manuel desea comprar un discman. Después de las averiguaciones que hizo, se enteró de que el precio es superior a $100.000, pero inferior a $150.000. El papá prometio colaborarle con la mitad del valor. Juan Manuel tiene ahorrado la cuarta parte; si la mamá le regala $20.000, ¿cuánto dinero reúne Juna Manuel?
El enunciado anterior tiene mucha información que podemos analizar con más cuidado, si usamos el lenguaje de la matemática para expresarlo.
Si el precio desconocido del discman se representa con la letra x, las diversas situaciones enunciadas en el problema también se puede expresar con ella y con números, tal como lo muestra la tabla.
Situación | Expresión verbal | Expresión matemática |
Precio del discman | Mayor que $100.000 y menor que $150.000 | |
Dinero que le da el papá | La mitad del precio | |
Dinero ahorrado por Juan Manuel | La cuarta parte del precio del discman | |
Dinero que le da la mamá | La mamá le regala $20.000 | $20.000 |
Dinero que tiene para la compra | Lo que le da el papá, lo ahorrado por Juan Manuel, lo que le regala la mamá. |
La letra que usamos para representar la cantidad desconocida está combinada con números a través de las operaciones de adición y sustracción, multiplicación y división. Esas operaciones, junto con la potenciación y la radicación, son llamadas operaciones algebraicas.
Se denomina expresión algebraica al conjunto de letras y números ligados entre sí por los signos de las operaciones algebraicas.
Ejemplos de expresiones algebraicas son:
Con expresiones algebraicas se enuncian las leyes de la física y la química, las fórmulas del perímetro, el área de las figuras geométricas, el volumen de los cuerpos, etc. Entre estas tenemos:
- la distancia d recorrida por un móvil que lleva una velocidad v durante un tiempo t es: d = v * t
 , donde h representa la constante de plank; m la masa del electrón; v la velocidad de desplazamiento del electrón.
, donde h representa la constante de plank; m la masa del electrón; v la velocidad de desplazamiento del electrón.
Ejemplo:
Si a, b y c son números reales, para cada expresión verbal encontremos su respectiva expresión algebraica.
a) El doble de la suma de a, b y c
b) La suma del doble de a y el triple de b
c) El cuadrado de la suma de a, b y c
d) La suma de los cuadrados de a, b y c
e) El producto de a por el cuadrado de c
f) La enésima potencia de la suma de a y b
Solución:
a) 2(a + b + c)
b) 2a + 3b
Video de profundización sobre conceptos importantes:
Fuente: http://www.youtube.com/watch?v=NYz6PEEdY4M
Polinomios
Monomio es una expresión algebraica que solamente contiene productos de números reales y de potencias de una o varias variables, cuyos exponentes son números enteros positivos.
Expresiones como  ,
, 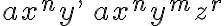 , se denominan monomios.
, se denominan monomios.
a es el coeficiente y  la parte literal.
la parte literal.
Por ejemplo  es un monomio con
es un monomio con  y
y  como parte literal, y
como parte literal, y  como coeficiente;
como coeficiente;  es un monomio en la variable
es un monomio en la variable  , con
, con  como parte literal y
como parte literal y  como coeficiente;
como coeficiente;  no es un monomio, ya que la variable
no es un monomio, ya que la variable  tiene exponente entero negativo.
tiene exponente entero negativo.
Ejemplo:
¿Cuáles expresiones:  , son monomios?
, son monomios?
Sólo 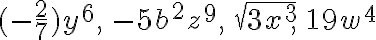 son monomios,; las demás no lo son, porque el exponente de la parte literal de
son monomios,; las demás no lo son, porque el exponente de la parte literal de 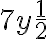 no es un número natural, lo mismo que ocurre con
no es un número natural, lo mismo que ocurre con 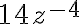 ya que la variable
ya que la variable 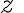 tiene exponente entero negativo.
tiene exponente entero negativo.
Cada monomio es un término y los monomios como 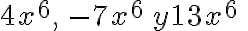 que tienen la misma parte literal, se llaman términos semejantes.
que tienen la misma parte literal, se llaman términos semejantes.
Dos monomios son semejantes cuando tienen la misma parte literal.
En la expresión  se ha indicado una suma algebraica de términos semejantes, la cual puede simplificarse usando la propiedad distributiva, así:
se ha indicado una suma algebraica de términos semejantes, la cual puede simplificarse usando la propiedad distributiva, así:
De este modo la expresión se ha reducido a un solo monomio.
Para adicionar términos semejantes se adicionan algebraicamente sus coeficientes y el resultado se multiplica por la parte literal. Este proceso se denomina reducción de términos semejantes.
Grado de un monomio
Los monomios  no son semejantes a pesar de tener la misma variable.
no son semejantes a pesar de tener la misma variable.
Se diferencian no sólo por el coeficiente, sino por el exponente de la variable. En el primer caso el exponente es 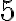 , en el segundo el exponente es
, en el segundo el exponente es  ; por esta razón se dice que el grado del primer monomio es
; por esta razón se dice que el grado del primer monomio es 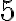 y del segundo es
y del segundo es  .
.
Cuando un monomio tiene varias variables, su grado corresponde a la suma de los exponentes de las variables que lo forman. Así, 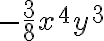 es un monomio de grado
es un monomio de grado  .
.
Se llama grado de un monomio al exponente de la variable si el monomio tiene una sola variable, o la suma de los exponentes de las variables cuando el monomio cuenta con varias variables. El coeficiente del monomio debe ser distinto de cero.
Polinomio en una variable
Las expresiones 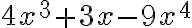 y
y  indican una suma de monomios con la misma variable.
indican una suma de monomios con la misma variable.
Una suma algebraica de varios monomios se denomina polinomio. Cada monomio constituye un término del polinomio.
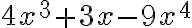 es un polinomio en la variable
es un polinomio en la variable  de tres términos y
de tres términos y  es un polinomio en la variable y que tiene cuatro términos. Además el término que no contiene y, en este caso
es un polinomio en la variable y que tiene cuatro términos. Además el término que no contiene y, en este caso 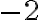 , decimos que es de grado cero y se llama término independiente o constante.
, decimos que es de grado cero y se llama término independiente o constante.
Cuando los monomios que forma el polinomio tienen más de una variable como 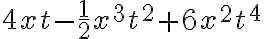 , se tiene un polinomio en las variables x y t.
, se tiene un polinomio en las variables x y t.
Cuando un polinomio contiene sólo dos términos se llama binomio. Si contiene tres términos es un trinomio.
Los polinomios  y
y  son binomios;
son binomios;  y
y  son trinomios.
son trinomios.
En general un polinomio en una variable es una expresión de la forma  , con
, con 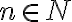 . Si
. Si  , se dice que el grado del polinomio es
, se dice que el grado del polinomio es  .
.
Ejemplo:
 es un polinomio en las variables
es un polinomio en las variables  y
y  . El grado del polinomio es
. El grado del polinomio es 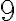 .
.
Cuando los términos de un polinomio se escriben de modo que sus grados vayan creciendo o decreciendo, se dice que el polinomio está ordenado. Por ejemplo  está ordenado respecto a las potencias creciente de
está ordenado respecto a las potencias creciente de  ;
; 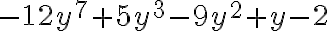 está ordenado respecto a las potencias decrecientes de
está ordenado respecto a las potencias decrecientes de  .
.
El polinomio  es un polinomio ordenado, en donde aparece un término de cada grado desde cero hasta cinco. Por esto se llama polinomio completo de grado 5. Si al polinomio le falta alguno de sus términos, se le llama polinomio incompleto.
es un polinomio ordenado, en donde aparece un término de cada grado desde cero hasta cinco. Por esto se llama polinomio completo de grado 5. Si al polinomio le falta alguno de sus términos, se le llama polinomio incompleto.
 es un polinomio incompleto de sexto grado.
es un polinomio incompleto de sexto grado.
PREGUNTA: ¿Cuál es el grado del polinomio 
Grado 4 Grado
7 Grado 17 Grado 6
Adición y sustracción de polinomios
Una fábrica produce las baldosas que aparecen en la figura, con los cuales elabora distintos patrones.
Algunos de los patrones construidos son los que se muestran en la figura.
Un arquitecto necesita saber el área de cada patrón para decidir cómo acomodarlos en el piso.
primero hallemos el área de cada baldosa.
Veamos ahora el área de cada patrón.
El área de cada patrón corresponde a un polinomio.
si los valores de x y y son 20cm y 10cm respectivamente, el área del patrón c. es:
Si se desea unir los patrones  ,
,  ,
,  , el área de la región cubierta por ellos sera la suma de sus áreas:
, el área de la región cubierta por ellos sera la suma de sus áreas:
Reduciendo término semejantes obtuvimos otro polinomio.
Si queremos averiguar en cuanto difieren las áreas de los patrones b. y c., se tiene:
Se eliminan paréntesis y se reducen los términos semejantes. Al hacer la diferencia de polinomios se tienen en cuenta las reglas vistas en la sustracción de números reales.
Si como se dijo antes, los valores de x y y son 20cm y 10 cm, la diferencia entres las áreas de los patrones b. y c. es:
Así como en los enteros se puede convertir la sustracción en una adición con el opuesto, en los polinomios se puede proceder de manera similar. El opuesto de un polinomio es el polinomio que tiene los mismos coeficientes del polinomio dado, cambiados de signo.
Por ejemplo hallemos la diferencia de los polinomios  y
y 
Escribimos
PREGUNTA: Efectuar la adición de los polinomios
Polinomio 3: 
A) 5x^3+2x^2 + 5x +14 B) 5x^3-2x^2 + 5x -14
Multiplicación de polinomios
En los monomios  , como
, como  son variables que toman valores en los números reales, realizar la multiplicación entre los monomios es similar a efectuar la multiplicación entre números reales.
son variables que toman valores en los números reales, realizar la multiplicación entre los monomios es similar a efectuar la multiplicación entre números reales.
Por ejemplo:
El producto de dos monomios es otro monomio en el que se cumple:
- El coeficiente es el producto de los coeficientes de los factores
- La parte literal corresponde al producto de la(s) variable(s) que aparecen en los monomios. En este producto se aplica a la ley de los exponentes para potencias de igual base.
- El grado del monomio producto es igual a la suma de los grados de los monomios factores.
Si se tienen más de dos monomios, para hallar con ellos el producto se procede de igual manera que cuando hay dos monomios.
Ejemplo:
¿Cuál es el producto de los monomios 
Solución:
Si uno de los factores es un polinomio, para obtener el producto se hace uso de la propiedad distributiva y se multiplica el monomio por cada término del polinomio.
Ejemplo:
Para multiplicar un polinomio por un monomio se efectua el producto del monomio por cada uno de los términos del polinomio.
El grado del polinomio corresponde a la suma de los grados del polinomio y del monomio. En le ejemplo anterior se tiene:
Los polinomios también se pueden disponer en columnas para realizar la multiplicación.
Cuando los polinomios se ordenan y se disponen en columnas, se consiguen los productos parciales del primero por cada término del otro; luego se suman los resultados.
Para hallar el producto de varios polinomios se hace uso de la propiedad asociativa de la multiplicación de números reales.
Ejemplo:
¿Cuál es el valor de A*B*C si 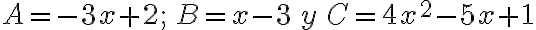 ?
?
Se calcula primero el producto de dos polinomios y ese resultado se multiplica por el tercer polinomio.
El grado del polinomio producto es la suma de los grados de los polinomios factores.
En el ejemplo anterior para hallar A*B*C calculamos primero el producto A*B y luego lo multiplicamos por C. Si hallamos primero B*C y luego a Alo multiplicamos por ese producto, obtendremos el mismo resultado.
a) 5x^9+3x^6y^2+x^5y^3+15x^4y^4+9xy^5+3y^7
b) 5x^9+3x^6y^2+x^5y^3+15x^4y^4+9xy^5+3y^6
c) 5x^9+3x^6y^2+x^5y^3+15x^4y^4+9x^3y^6+3y^7
d) 5x^9+3x^6y^2+x^5y^3+15x^4y^4+9xy^6+3y^7
Expresiones notables
Son aquellos productos que se rigen por reglas fijas y cuyo resultado puede hallarse por simple inspección. Son denominados también "Identidades Algebraicas". Son aquellos productos cuyo desarrollo es clásico y por esto se le reconoce fácilmente. Las más importantes son:
Binomio de suma al cuadrado: El cuadrado de la suma de dos términos es igual al cuadrado del primer término, más el doble producto de ambos, más el cuadrado del segundo.
Binomio diferencia al cuadrado: El cuadrado de la diferencia de dos términos es igual al cuadrado del primero, menos el doble del producto de ambos, más el cuadrado del segundo término.
Ejemplo:
Diferencia de cuadrados: El producto de dos términos por la diferencia de los mismos, es igual al cuadrado del primero menos el cuadrado del segundo.
Ejemplo:
Binomio suma al cubo: El cubo de la suma de los dos términos es igual al cubo del primer término, más tres veces el cuadrado del primero por el segundo, más tres veces el primero por el cuadrado del segundo, más el cubo del segundo.
Ejemplo:
Binomio diferencia al cubo: El cubo de la diferencia de dos términos es igual al cubo del primer término, menos tres veces el cuadrado del primero por el segundo, más tres veces el primero por le cuadrado del segundo, menos el cubo del segundo.
Producto de dos binomios que tienen un término común:
a) x^3-6x^2+12x-8 b)
x^3+6x^2+12x-8 c) x^3+6x^2-12x+8 d) x^3-6x^2+12x+8
División de polinomios
Recordemos algunas formas de expresar cocientes:
Si  son números reales, entonces:
son números reales, entonces:
Ahora recordemos algunas propiedades de la potenciación.
Si 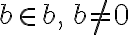 , y
, y 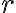 ,
,  son enteros positivos, se tiene:
son enteros positivos, se tiene:
Ejemplo 1:
Solución:
El resultado del ejemplo muestra que para cualquier valor de 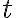 y
y 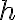 con
con  y
y 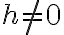 , la expresión
, la expresión  tiene los mismos valores que
tiene los mismos valores que  . Cuando remplazamos a
. Cuando remplazamos a  por
por  , decimos que se ha dividido
, decimos que se ha dividido  por
por  y a
y a  lo llamamos el cociente de los monomios. También decimos que se ha simplificado la expresión
lo llamamos el cociente de los monomios. También decimos que se ha simplificado la expresión  .
.
Un monomio es divisible por otro si el exponente de las variables del dividiendo y divisor, al simplificar, hacen que el cociente sea un monomio.
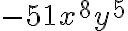 es divisible por
es divisible por  porque el cociente
porque el cociente  es un monomio. Para que el cociente de dos monomios sea otro monomio se requiere que le dividiendo contenga la(s) variable(s) del divisor con el exponente(s) mayor(es) o igual(es).
es un monomio. Para que el cociente de dos monomios sea otro monomio se requiere que le dividiendo contenga la(s) variable(s) del divisor con el exponente(s) mayor(es) o igual(es).
Los cocientes:  no se reducen a monomios.
no se reducen a monomios.
División de un polinomio por un monomio
Analicemos el siguiente ejemplo:
Para dividir un polinomio por un monomio se divide cada término por el monomio, y se suman los cocientes particulares.
División de dos polinomios
Recordemos el proceso de división entre dos enteros:
Se puede verificar que: 951-(35)(27)=6 0 que 951=(35)(27)+6
En general se tiene:
Dividiendo - (Divisor x Cociente) = Residuo
Dividiendo = (Divisor x Cociente) + Residuo
Esta igualdad es equivalente a:
Para el ejemplo numérico se tiene:  .
.
Así como el cociente de dos enteros se llama numero racional, si el denominador es distinto de 0, el cociente de dos polinomios se llama expresión racional.
Ejemplo 2:
Solución:
El resultado se puede escribir así:
Se puede comprobar que:
Ejemplo 3:
El resultado puede escribirse así:
Se puede comprobar que:
En este ejemplo ha sido conveniente completar el polinomio dividiendo  en la forma
en la forma  , para facilitar el algoritmo de la división.
, para facilitar el algoritmo de la división.
Para dividir un polinomio por otro:
· Ordenamos ambos polinomios según las potencias decrecientes de la misma variable, dejando espacios para los términos faltantes en caso que el polinomio dividiendo sea incompleto.
· Obtenemos el primer término del cociente: dividiendo el primer término del dividiendo por el primer divisor.
· Obtenemos el primer dividiendo parcial: multiplicamos el primer término del cociente por el divisor y el producto se resta del dividiendo.
· Repetimos el proceso hasta obtener un dividiendo parcial cuyo grado sea menor al del divisor. Este dividiendo parcial será el residuo.
Ver el siguiente video explicativo, con el procedimiento de la división de polinomios:
División sintética
Realicemos la siguiente división entre los polinomios 
Las expresiones las podemos reducir si se omiten las potencias de la variable y trabajamos sólo con los coeficientes, ya que es la posición que indica el grado del término, y lo que cambia son los coeficientes. Al hacer eso la división anterior toma la siguiente forma:
Si analizamos el proceso anterior notamos que el primer número de cada producto parcial se anula al hacer la sustracción. Pero esto no influye a los residuos parciales. Podemos omitir los términos del cociente y los primeros términos de los productos parciales. Haciéndolo, tenemos:
Como el polinomio divisor es de la forma  , o se le puede reducir a ella, el primer coeficiente del divisor es
, o se le puede reducir a ella, el primer coeficiente del divisor es 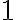 y, por lo dicho antes, al hacer los productos parciales por tal coeficiente y restar del residuo parcial, estos términos se anulan. Por tanto, se puede eliminar a
y, por lo dicho antes, al hacer los productos parciales por tal coeficiente y restar del residuo parcial, estos términos se anulan. Por tanto, se puede eliminar a 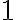 del divisor y trasladar los residuos parciales hacia arriba. Conservando la columna, quedando organizados así:
del divisor y trasladar los residuos parciales hacia arriba. Conservando la columna, quedando organizados así:
Para completar esta forma de dividir se escribe 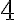 , primer coeficiente del dividiendo, en el primer lugar de la línea inferior. De este modo, se tiene:
, primer coeficiente del dividiendo, en el primer lugar de la línea inferior. De este modo, se tiene:
Los números de la segunda línea se obtienen multiplicando por 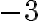 , el número de la línea inferior de la columna precedente.
, el número de la línea inferior de la columna precedente.
Los números de la línea inferior se obtienen restando los números de la segunda línea, columna con columna, de los de la línea superior.
Si el multiplicador 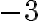 se remplaza por
se remplaza por 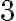 , su opuesto, los números de la segunda línea se pueden sumar con los de la línea superior para obtener los de la línea inferior. Haciendo, el cambio queda:
, su opuesto, los números de la segunda línea se pueden sumar con los de la línea superior para obtener los de la línea inferior. Haciendo, el cambio queda:
El proceso anterior, llamado división sintética, es válido en los casos en los que el divisor es de la forma  y se puede resumir así:
y se puede resumir así:
1. Ordenamos el polinomio dividiendo así:
 Si el polinomio no es completo, escribimos coeficiente cero a los términos que hacen falta.
Si el polinomio no es completo, escribimos coeficiente cero a los términos que hacen falta.
2. Escribimos los coeficientes del polinomio en orden, incluso los que valgan cero, en una línea horizontal.
3. Trasladamos el primer coeficiente del polinomio a la línea inferior.
4. Multiplicamos 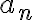 por
por 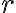 y escribimos el producto en la segunda línea, debajo del coeficiente
y escribimos el producto en la segunda línea, debajo del coeficiente 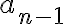 . Adicionamos el producto a
. Adicionamos el producto a 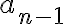 y el resultado lo escribimos en la línea inferior.
y el resultado lo escribimos en la línea inferior.
5. Multiplicamos la suma anterior por 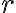 y el producto lo escribimos en la segunda línea, debajo del coeficiente
y el producto lo escribimos en la segunda línea, debajo del coeficiente  . Adicionamos el producto a
. Adicionamos el producto a  y escribimos el resultado en la linea inferior.
y escribimos el resultado en la linea inferior.
6. Repetimos lo dicho en 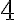 y
y 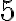 . Hasta donde sea posible.
. Hasta donde sea posible.
7. El último número de la linea inferior es el residuo, y los números, a su izquierda, son los coeficientes del polinomio cociente, cuyo grado es inferior en uno al grado del polinomio dividiendo.
Ejemplo 1:
Solución:
Los coeficientes del dividiendo son:  , o y
, o y  .
.
Factorizacion
Factor Común
Cuando se multiplica dos o más números para formar un producto, cada número se llama factor del producto. Recordemos que la palabra factor está ligada a la operación multiplicación.
Para determinar todos los factores enteros de un número, se usa la descomposición en factores primos del número y con estos se construye un diagrama de árbol, como se muestra en el esquema de la figura. El producto de los números en cada rama es un factor del número original.
Para determinar factores que no sean enteros se divide el entero por cualquier número diferente de cero. Entonces el cociente y el divisor son factores del entero. Por ejemplo, factores de 12 son 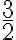 y 8, ya que
y 8, ya que  , es decir
, es decir 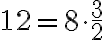
Ejemplo:
Se quiere entapetar una oficina de 4 m por 5 m usando dos piezas rectangulares de alfombra; una de ellas tiene 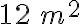 de área y la otra
de área y la otra 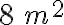 . ¿Puede hacerse sin cortar las piezas?
. ¿Puede hacerse sin cortar las piezas?
Como veremos, para responder esta pregunta necesitamos más información. El área de la primera pieza de tapete es 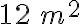 , pero puede tener varias formas. Por ejemplo:
, pero puede tener varias formas. Por ejemplo:
Esto se debe a que 12, 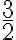 y 3 son algunos de los factores de 12.
y 3 son algunos de los factores de 12.
Para poder usar los dos pedazos de alfombra sin cortarlos, uno de los lados de cada rectángulo debe tener igual medida. Como las dimensiones del piso son 4 m y 5 m, esos valores son las posibles medidas del lado común. Además, tomando en cuenta el área de los dos pedazos de alfombra, la medida común debe ser factor común de 8 y 12. Veamos
Para encontrar el máximo entero factor común de dos o más números enteros se escogen los factores primos comunes con el menor exponente con el cual aparecen en la descomposición en factores primos de cada número.
Ejemplo :
¿Cuál es el máximo factor común de 24 y 120?
Como 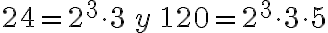 , entonces, el máximo factor común es
, entonces, el máximo factor común es 
Cuando queremos hallar factores comunes de monomios con coeficientes enteros, procedemos de igual forma. Escogemos, además de cada primo común de los coeficientes con el menor exponente.
El máximo factor común de dos o más monomios es el monomio factor común con el mayor coeficiente y mayor grado en cada variable.
Ejemplo:
¿Cuál es el máximo factor común de 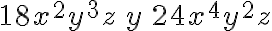 ?
?
· Hacemos la descomposición en factores primos de 18 y 24 para determinar el máximo factor común de los coeficientes.
Por tanto, el máximo factor común de 18 y 24 es 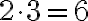
· Ahora encontramos el mayor factor común de la parte literal de los monomios, es decir 
En este caso el mayor factor común es: 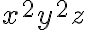
· Por ultimo determinamos el mayor factor común de los monomios así: 
Es importante saber cuál es el máximo factor común de dos o más monomios, porque nos ayuda a simplificar fracciones, cuyo numerador y denominador son monomios, o a expresar una suma algebraica de monomios como producto. Al máximo factor común se acostumbra llamarlo simplemente factor común.
Ejemplo:
Simplifiquemos la fracción 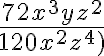 , donde
, donde 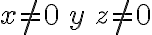 .
.
· Descomponemos en factores primos los coeficientes:  . Determinamos el factor común :
. Determinamos el factor común : 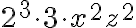
Expresamos tanto el numerador como el denominador en forma de producto (factorizamos), en donde uno de los factores es el máximo factor común, esto es:
· Finalmente simplificamos la fracción:
Ejemplo 2:
Supongamos que tengamos tres rectángulos cuyas áreas son  . Los tres rectángulos tienen un lado con la misma medida, la cual es el máximo monomio factor común de los monomios que denotan las áreas. ¡Cuales son las dimensiones del rectángulo que se obtiene al unir los tres rectángulos por el lado de medida común?
. Los tres rectángulos tienen un lado con la misma medida, la cual es el máximo monomio factor común de los monomios que denotan las áreas. ¡Cuales son las dimensiones del rectángulo que se obtiene al unir los tres rectángulos por el lado de medida común?
Antes de comenzar a resolver el problema, conviene expresar todos los números con un denominador común, para que en el monomio factor común se encuentren los fraccionarios:
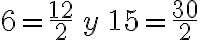 ahora realicemos los siguientes pasos:
ahora realicemos los siguientes pasos:
· Descomponemos en factores primos los numeradote:
· Determinamos el factor común: 
· Factorizamos cada monomio:
· Determinamos las dimensiones del rectángulo, como se ve en la figura.
Por tanto, las dimensiones de los lados del rectángulo son 
Lo anterior indica que el área de ese rectángulo esta dada por:
 . Esta ultima expresión es la factorización del polinomio
. Esta ultima expresión es la factorización del polinomio 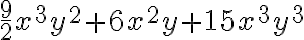 , el cual corresponde a la suma de las áreas de los tres rectángulos.
, el cual corresponde a la suma de las áreas de los tres rectángulos.
Un polinomio se factoriza cuando se expresa como el producto de otros polinomios
Si el polinomio tiene coeficientes enteros, su factorización debe ser con polinomios de coeficientes enteros. Si el polinomio tiene coeficientes racionales, se factoriza inicialmente el numero racional correspondiente, para que el polinomio restante tenga coeficientes enteros. Para factorizar un polinomio se debe usar, como uno de los factores, el máximo monomio factor común de los monomios que conforman el polinomio y la propiedad distributiva.
Ejemplo:
Factorizar el siguiente polinomio 
El polinomio tiene coeficientes racionales, entonces:
· Factorizamos el numero racional correspondiente: 
· Descomponemos en factores primos los coeficientes: 
· Determinamos el factor común:  .
.
Podemos comprobar si la factorización es correcta multiplicando los factores que resultan.
PREGUNTA: El factor común de:  es:
es:
Factorización por agrupación.
FACTOR COMÚN POR AGRUPACIÓN DE TÉRMINOS
Para poder comprender este procedimiento se realizarán varios ejemplos que desarrollarán el ejercicio en busca de encontrar el factor común de la expresión.
Los dos primeros términos tienen el factor común  y los dos últimos el factor común y agrupamos los dos primeros términos en un paréntesis y los dos últimos en otro precedido del signo
y los dos últimos el factor común y agrupamos los dos primeros términos en un paréntesis y los dos últimos en otro precedido del signo  por que el tercer término tiene el signo
por que el tercer término tiene el signo  y tendremos;
y tendremos;
La agrupación puede hacerse generalmente de más de una modo con tal que los dos términos que se agrupan tengan algún factor común, y siempre que las cantidades que quedan dentro de los paréntesis después de sacar el factor común en cada grupo, sean exactamente iguales. Si esto no es posible lograrlo la expresión dada no se puede descomponer por este método.
Los dos primeros términos tienen el factor común  y los dos últimos el factor común
y los dos últimos el factor común 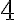 . Agrupando, tenemos:
. Agrupando, tenemos:
Factorización trinomios cuadráticos de la forma ax^2+bx+c (ac<0)
FACTORIZAR TRINIMIOS DE LA FORMA  ac<0
ac<0
En la leccion anterior vimos como factorizar trinomios donde  . si
. si  era positivo, los dos números que buscabamos eran positivos, pero si
era positivo, los dos números que buscabamos eran positivos, pero si  era negativo, los dos números debian ser negativos.
era negativo, los dos números debian ser negativos.
Ahora estudiaremos el caso en el cual ac < 0. Al descomponer c en factores primos recordemos que ubicamos en forma vertical primero el mayor y luego el menor. Como los dos números que debemos buscar deben ser de signo opuesto, es decir, uno positivo y uno negativo, colocamos el signo negativo al mayor de ellos.
Ejemplo:
Solución:
c<0 entonces ac<0
Ejemplo 2:
Solución:

Factorización trinomios cuadráticos de la forma ax^2+bx+c (ac>0)
FACTORIAZACIÓN DE TRINOMIOS CUADRÁTICOS DE LA FORMA 
Para factorizar el trinomio  , con ac>0, debemos:
, con ac>0, debemos:
- Hallar los factores primos de a y de c.
- Ubicar de mayor a menor los factores primos de a y de menor a mayor los factores primos de c en forma vertical (buscar 2 números que multiplicados me den a y después dos números que multiplicados me den c).
- Si
 es positivo, los dos números que buscamos serán positivos, pero si
es positivo, los dos números que buscamos serán positivos, pero si  es negativo, los dos numeros deben ser negativos.
es negativo, los dos numeros deben ser negativos. - Multiplicar en cruz los factores primos de a y de c.
- Sumar el resultado de ésta multiplicación
- Corroborar que el resultado de dicha suma sea x
- Realizar adición de los factores primos de ax y c en línea recta horizontal.
Ejemplo 1:
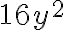 |  |  |  |  | |
| 8y | 3 | 6y | |||
| 2y | 9 | 72y | |||
 |
Ejemplo 2:
1. Hallamos los factores primos de a y de c
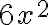 |  |  |  |  | |
| 3x | 2 | 4x | |||
| 2x | 3 | 9x | |||
 |
Ejemplo 3:
Solución:
Este trinomio es de la forma 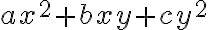 . Por tanto, el proceso es el mismo.
. Por tanto, el proceso es el mismo.
Si no es posible hallar los dos números que sumados den  , a partir de los factores de a$, decimos que el polinomio es primo.
, a partir de los factores de a$, decimos que el polinomio es primo.
Un polinomio que no puede expresarse como producto de polinomios de menor grado, es irreducible. Si el polinomio tiene coeficientes enteros que son relativamente primos y es además irreducible, decimos que es primo.
GRADO NOVENO
La recta Numérica real
El conjunto de los números naturales  , el conjunto de los números enteros
, el conjunto de los números enteros 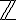 y el conjunto de los números racionales
y el conjunto de los números racionales  , pueden representarse en la misma recta numérica.
, pueden representarse en la misma recta numérica.
Para hacerlo trazamos una recta, como la de la figura, escogemos un punto fijo 0, llamado origen, una unidad de longitud y una dirección positiva.
Luego establecemos una correspondencia que asocia a cada entero un punto sobre la recta h, como muestra la figura. Dicha recta se conoce como recta númerica de los enteros.
Los números racionales también podemos representarlos en una recta numérica como la de la figura, si suponemos que un segmento puede dividirse en cualquier número de partes iguales.
En general podemos afírmar que:
Si a es un número asociado a un punto P sobre una recta h con una escala númerica, a se llamará la coordenada de P.
De esta manera se asocian dos conjuntos: una recta geométrica y un conjunto numérico, mediante una correspondencia uno a uno.
A cada número real a le corresponde un punto y sólo un punto de h; y recíprocamente a cada punto P de la recta h le corresponde exactamente un número real. Por esta razón se dice que el conjunto de los números reales es completo.
h se denomina recta coordenada o recta numérica real. Los números que corresponden a puntos que están a la derecha de 0 se llaman números reales positivos y se denota R+; los números que corresponden a puntos a la izquierda de 0 se llaman números reales negativos y se denotan R-. El número 0 no es ni positivo ni negativo.
La recta numérica ilustra gráficamente el orden de los números reales; si x y z son dos números reales y x < z, entonces el punto con la coordenada x queda a la izquierda del punto con la coordenada z. Por tanto, podemos decir que los números reales son un conjunto ordenado y completo.
Valor Absoluto
Cualquier número  tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto
tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto  al origen (0), sobre la recta.
al origen (0), sobre la recta.
Ejemplo 1:
Calculemos la distancia desde el origen hasta el punto 4 y al punto -4.
En la recta l, de la figura, vemos que:
 es:
es:  si
si  es positivo,
es positivo, 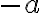 si
si  es negativo y 0 si
es negativo y 0 si  es cero. En forma simbólica lo escribimos:
es cero. En forma simbólica lo escribimos:
Ejemplo 2:
Solución:
 y
y  de una recta numérica, la distancia entre ambos es
de una recta numérica, la distancia entre ambos es  si
si 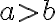 y
y 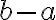 si
si  , es decir, la distancia entre ellos es
, es decir, la distancia entre ellos es 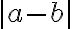 .
.
 , tal como lo observamos en la figura.
, tal como lo observamos en la figura.
Puede profundizar la lección, con los videos siguientes:
Fuente:
Ecuaciones e inecuaciones con valor absoluto
El valor absoluto lo encontramos con frecuencia en ecuaciones con polinomios reales de la forma  , en donde
, en donde 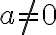 . En esos casos hallamos el conjunto solución aplicando la definición de valor absoluto.
. En esos casos hallamos el conjunto solución aplicando la definición de valor absoluto.
Ejemplo:
Solución:
Teniendo en cuenta las dos condiciones de la definición de valor absoluto,  queda resuelto cuando:
queda resuelto cuando:
x - 2 = 5 o x - 2 = -5
Para solucionar cada ecuación debemos sumarle 2 a ambos miembros de las igualdades:
x = 5 + 2 o x = - 5 + 2. Así se obtiene:
x = 7 o x = - 3
Ejemplo 2:
Encontremos el conjunto solución de 
Por la definición de valor absoluto tenemos:  . Resolviendo cada ecuación se sabe que
. Resolviendo cada ecuación se sabe que 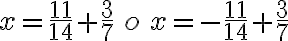 , de donde
, de donde  .
.
El conjunto solución de la ecuación 
No siempre existe solución para las ecuaciones con valor absoluto; por ejemplo la ecuación 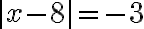 no tiene solución, puesto que el valor absoluto nunca es negativo.
no tiene solución, puesto que el valor absoluto nunca es negativo.
Para resolver desigualdades con valor absoluto usaremos un método muy parecido al empleado para resolver ecuaciones.
Consideremos primero la desigualdad de la forma 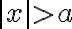 . Si a es negativo o cero, la inecuación es verdadera para todo x por definición de valor absoluto. Si a es positivo, esta desigualdad se intrpreta geometricamente como la distancia desde x hasta cero, la cual es mayor que a, esto es
. Si a es negativo o cero, la inecuación es verdadera para todo x por definición de valor absoluto. Si a es positivo, esta desigualdad se intrpreta geometricamente como la distancia desde x hasta cero, la cual es mayor que a, esto es  . Por tanto, tendremos que x > a o x > - a. Por ejemplo, la inecuación
. Por tanto, tendremos que x > a o x > - a. Por ejemplo, la inecuación  es equivalente a la proposición x > 4 o x < - 4. La interpretación geometrica se muestra en la siguiente figura.
es equivalente a la proposición x > 4 o x < - 4. La interpretación geometrica se muestra en la siguiente figura.
Ejemplo:
Busquemos el conjunto solución de  .
.
para interpretar  como la distancia entre dos puntos, escribimos
como la distancia entre dos puntos, escribimos  .
.
Así el conjunto solución de  debe contener a todos los números reales x, tales que la distancia entre x y -5 sea mayor o igual a 2.
debe contener a todos los números reales x, tales que la distancia entre x y -5 sea mayor o igual a 2.
Por tanto, tendremos que:
La gráfica corresponde a la que se ve en la figura.
En las gráficas de estas desigualdades utilizamos el simbolo  para indicar que el punto pertenece al conjunto solución y el símbolo
para indicar que el punto pertenece al conjunto solución y el símbolo  cuando el punto no pertenece al conjunto solución.
cuando el punto no pertenece al conjunto solución.
Consideremos ahora la desigualdad de la forma 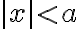 .
.
Puesto que  es un número no negativo, esta inecuación carece de solución cuando a es cero o negativo, por tanto, debe asumirse que a es positivo. Entonces la inecuación
es un número no negativo, esta inecuación carece de solución cuando a es cero o negativo, por tanto, debe asumirse que a es positivo. Entonces la inecuación 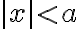 significa geométricamente que la distancia desde x hasta cero es menor que a. Es decir, x se encuentra ubicado entre los valores -a y a (excluidos los puntos extremos), lo cual queda expresado mediante la doble inecuación - a < x < a. así, la inecuación
significa geométricamente que la distancia desde x hasta cero es menor que a. Es decir, x se encuentra ubicado entre los valores -a y a (excluidos los puntos extremos), lo cual queda expresado mediante la doble inecuación - a < x < a. así, la inecuación  es equivalente a la dobl desigualdad -5 < x < 5. Veamos la interpretación geométrica en la figura.
es equivalente a la dobl desigualdad -5 < x < 5. Veamos la interpretación geométrica en la figura.
Exponentes y propiedades
Si  es en elemento positivo y
es en elemento positivo y  es cualquier número real, definimos
es cualquier número real, definimos  como el producto de
como el producto de  factores de
factores de  .
. 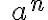 es la n-ésima potencia de
es la n-ésima potencia de  . Simbólicamente:
. Simbólicamente:
Si  es un número real y
es un número real y  es un número entero, tenemos:
es un número entero, tenemos:
 , donde
, donde  se llama exponente y
se llama exponente y  base.
base.
PROPIEDADES DE LA POTENCIACIÓN
De esta definición obtenemos las siguientes propiedades, llamadas leyes de los exponentes, que nos permitirán simplificar expresiones con exponentes.
Ejemplo:
Aplicando la definición de potencia n-ésima de  , podemos escribir:
, podemos escribir:
Ejemplo 2:
simplifiquemos,
Recordemos que las propiedades de los exponentes se aplican a productos y cocientes, y no a adiciones ni a sustraciones.
Tampoco podemos multiplicar o dividir dos potencias de bases diferentes usando las propiedades 1 o 4. Es decir,  no puede simplificarse mediante
no puede simplificarse mediante  , porque las bases no son iguales.
, porque las bases no son iguales.
Radicales y propiedades
Recordemos que la raiz cuadrada de un número  es un número no negativo
es un número no negativo  , tal que
, tal que  , es decir:
, es decir: 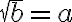 .
.
La raíz cúbica de un número  es un número
es un número  , tal que
, tal que 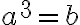 , es decir:
, es decir: ![\sqrt[3]{b}=a \sqrt[3]{b}=a](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/2014186b4942eaeb661ff296a83e6fb9.gif) .
.
Para definir la raíz n-ésima de un número decimos:  es una raíz n-ésima de
es una raíz n-ésima de  si
si  . Es decir:
. Es decir: ![\sqrt[n]{b}=a \sqrt[n]{b}=a](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b2480dff4dea5bb8f396c9367ebbdbac.gif)
PROPIEDADES DE LOS RADICALES
Los radicales podemos escribirlos como una potencia con exponente racional y les aplicamos las propiedades de los exponentes; de esta ,manera definimos las siguientes PROPIEDADES DE LOS RADICALES.
Al aplicar estas propiedades debemos tener precaución cuando x, .
.
Ejemplo: Propiedad 1
simplifiquemos.
Ejemplo 2: Propiedad 4
Ejemplo 3:
Simplificar y expresar con exponente positivo.
El siguiente video, le ayudará a profundizar el tema. Debe leerlo detenida y pausadamente, resolviendolo en la libreta de notas:
Fuente:http://www.youtube.com/watch?v=oQRf4lSIfY4
EJERCICIOS DE PRACTICA 1 Noveno
determinar qué tanto aprendiste los conceptos y procedimientos vistos en la unidad 1.
1.Calculo el valor absoluto.
2. Solucionar cada ejercicio con base en las propiedades del valor absoluto.
3. Encuentro el conjunto solución para cada ecuación:
4. Determina si es verdadera o falsa cada afirmación:
5. Simplifico cada expresión utilizando las propiedades de los exponentes.
6. Escribo las expresiones empleando exponentes.
7. Simplifico cada ejercicio
8. Racionalizo cada expresión
9. Escriban cada expresión en forma exponencial
10. Racionalizo el denominador de las expresiones
Los números complejos
Al resolver ecuaciones algebraicas, en los números reales, es evidente que toda ecuación de primer grado con incógnita x, puede reducirse a la forma 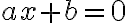
 y su solución únicas es el numero real
y su solución únicas es el numero real 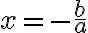 .
.
Si la ecuación es de segundo grado para la incógnita x, puede reducirse a la forma 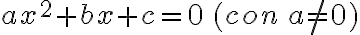 y en tal caso:
y en tal caso:
· Su conjunto solución tiene dos elementos, que son los números reales
 , siempre y cuando se cumpla que
, siempre y cuando se cumpla que 
· Su conjunto solución tiene un solo elemento, que es el número real 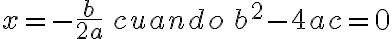
· Su conjunto solución no tiene elementos reales, es decir, la ecuación no tiene solución en los números reales si 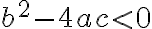 , por cuanto no existe un número real cuyo cuadrado sea un número negativo. Recordemos que
, por cuanto no existe un número real cuyo cuadrado sea un número negativo. Recordemos que 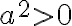 para todo número real
para todo número real  . (1)
. (1)
En particular la ecuación cuadrática  , que puede escribirse como
, que puede escribirse como  , tiene como soluciones
, tiene como soluciones  , números que no son reales.
, números que no son reales.
Así mismo resultado llegamos si toma la ecuación 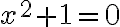 y escribimos
y escribimos  ; en tal caso, es necesario encontrar un numero cuyo cuadrado sea
; en tal caso, es necesario encontrar un numero cuyo cuadrado sea  ; de acuerdo con (1), es imposible que tal número sea real.
; de acuerdo con (1), es imposible que tal número sea real.
Los matemáticos llamaron “imaginarios” a los números cuyo cuadrado es un número negativo y posteriormente idearon el símbolo  , por
, por  comienza la palabra imaginario, para representar al numero cuyo cuadrado es
comienza la palabra imaginario, para representar al numero cuyo cuadrado es  , es decir, estableciendo que
, es decir, estableciendo que 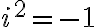
Como resultado tenemos que  no es un número real y además que el producto de un real por
no es un número real y además que el producto de un real por  tampoco es un número real.
tampoco es un número real.
Como en los números reales todo cuadrado es un numero real no negativo, la solución de la ecuación 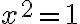 no es un numero real. Se acepta que existe un numero notado
no es un numero real. Se acepta que existe un numero notado  , que no es real, para le cual
, que no es real, para le cual 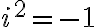 .
.
Ahora nos preguntamos: si adicionamos un número real con el producto de un real por  , ¿la suma
, ¿la suma  es un numero real?
es un numero real?
Un número de la forma  , en donde
, en donde  y
y  son números reales, no es un numero real. Todos los números de la forma
son números reales, no es un numero real. Todos los números de la forma  se llaman complejos. En un número complejo
se llaman complejos. En un número complejo  se llama parte real y
se llama parte real y  se llama parte imaginaria. Esta forma de representar a los números complejos se llama forma binomial, por cuanto puede considerarse
se llama parte imaginaria. Esta forma de representar a los números complejos se llama forma binomial, por cuanto puede considerarse  como un binomio algebraico.
como un binomio algebraico.
Dos números complejos son iguales cuando su parte real y su parte imaginaria, respectivamente son iguales.
Ejemplo:
Identifiquemos la parte real y la parte imaginaria de los números:  .
.
· Para el numero complejo 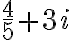 la parte real es
la parte real es 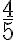 y la parte imaginaria es
y la parte imaginaria es 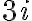
· Para el numero complejo  la parte real es
la parte real es 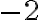 y la parte imaginaria es
y la parte imaginaria es 
· Para el numero complejo 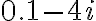 la parte real es 0.1 y la parte imaginaria es
la parte real es 0.1 y la parte imaginaria es 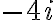
· Para el numero complejo  la parte real es
la parte real es  y la parte imaginaria es
y la parte imaginaria es 
Ejemplo 2:
¿Cuál es la parte imaginaria de los números 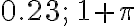 ?
?
Estos números son reales y, por tanto, “no tienen” parte imaginaria. Sin embargo, es importante anotar que le numero real  puede escribirse como
puede escribirse como  y se acepta que su parte imaginaria es
y se acepta que su parte imaginaria es  .
.
Todo numero real 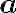 puede escribirse como el complejo
puede escribirse como el complejo  ; por tal razón, a todo numero real
; por tal razón, a todo numero real 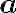 le corresponde la representación compleja
le corresponde la representación compleja  , en donde
, en donde  es su parte imaginaria. En este sentido se acepta que todo número real es un número complejo.
es su parte imaginaria. En este sentido se acepta que todo número real es un número complejo.
Ejemplo 3:
Para obtener la suma operamos las partes reales y las partes complejas por separado; el resultado
Si  y
y  son números reales, entonces:
son números reales, entonces:
Por tanto, la adición de dos números complejos es un numero complejo, cuya parte real es la asuma de la parte real de los sumandos y la parte imaginaria es la suma de la parte imaginaria de los sumandos.
Las propiedades de la adición de números complejos son las mismas que las de la adicción de los números reales.
Modulo de la adición de los números complejos
Si suponemos que le modulo tiene la forma  , entonces:
, entonces:
Luego 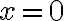 y
y  . En conclusión, el modulo de la adición de los complejos es el complejo
. En conclusión, el modulo de la adición de los complejos es el complejo 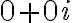 .
.
El módulo de la adición de los números complejos es el complejo 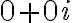 y el opuesto del complejo
y el opuesto del complejo  es el numero
es el numero 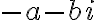 .
.
PREGUNTA: Al realizar la operación 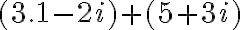 el resultado es:
el resultado es:
Solución de sistemas de ecuaciones: método gráfico
Dos o más ecuaciones con las mismas incógnitas, forman un sistema de ecuaciones.
La solución de un sistema con las incognitas x y y es el par ordenado(a,b) que hace verdaderas las dos ecuaciones.
Cuando un sistema de ecuaciones tiene solución, se dice que es consistente, de lo contrario, se llama inconsistente.
Las ecuaciones 2x + 3y = 18 y -x + 2y = -2 forman un sistema de dos ecuaciones con dos incógnitas, x y y.
Hallemos, mediante gráficas, la solución del sistema:
Grafiquemos las funciones 4x - y = -5 y 3x + 4y = 1 en un mismo plano cartesiano.
En la figura observamos que el único punto que pertenence a ambas líneas rectas es (-1,1); eso significa que la pareja (-1,1) es la solución del sistema. Verifiquémoslo remplazando a x por -1 y a y por 1 en ambas ecuaciones. se trata de un sistema consistente.
| 4x - y = -5 | 3x + 4y = 1 |
| 4(-1) - (1) = -5 | 3(-1) + 4(1) = 1 |
Solucionar, mediante gráficas, el sistema:
Al trazar la gráfica de las ecuaciones en el mismo plano cartesiano, como se hizo en la figura, observamos que las dos rectas tienen igual pendiente  y distinto punto de corte con el eje Y (y-intersecto). Como las rectas son paralelas. no se intersectan, por tanto, no hay un par ordenado que sea la solución de ambas ecuaciones. Ene stos casos se dice que el sistema no tiene solución. Es un sistema inconsistente.
y distinto punto de corte con el eje Y (y-intersecto). Como las rectas son paralelas. no se intersectan, por tanto, no hay un par ordenado que sea la solución de ambas ecuaciones. Ene stos casos se dice que el sistema no tiene solución. Es un sistema inconsistente.
resolvamos en forma gráfica el sistema:
Al trazar la gráfica de las ecuaciones en un mismo plano, observamos que las rectas coinciden. Se dice entonces que las ecuaciones son equivalentes porque cada una puede obtenerse de la otra mediante la multiplicación o división de sus miembros por un mismo número, diferente de cero, formando así un sistema consistente, con un número infinito de soluciones.
En el siguiente vídeo puedo observar un ejemplo resuelto:
Dirección url del vídeo: http://www.youtube.com/watch?v=ieiRIATCOUI
PREGUNTA: ¿En el método gráfico que sucede cuando dos gráficas coinciden?
Método de sustitución
Existen numerosas situaciones de la vida real que dan lugar a la formulación de sistemas de ecuaciones, cuyo resultado no es un par de números enteros. En tal caso, la solución del sistema por el método gráfico no es muy exacta. Es necesario entonces recurrir a otros métodos para solucionar sistemas, entre ellos el de la sustitución, el cual estudiaremos a continuación.
Para solucionar sistemas de ecuaciones por sustitución realizamos los siguientes pasos.
Paso 1: Despejamos una de las dos incógnitas en cualquiera de las dos ecuaciones.
Paso 2: Sustituimos la expresión hallada, en el paso anterior, en la otra ecuación del sistema y despejamos la incógnita.
Paso 3: Remplazamos el resultado que encontramos en el paso 2 en la ecuación del paso 1 y hallamos el valor correspondiente a la otra incógnita.
Paso 4: Verificamos los valores encontrados para las incógnitas remplazándolas en cada ecuación.
Ejemplo:
Resolvamos por el método de sustitución, el sistema de ecuaciones:
Paso 1. Despejamos a x de la ecuación (2)
Paso 2. Sustituimos la expresión de x en la ecuación (1)
Resolvemos las operaciones:
Paso 3. Sustituimos el valor de y en la ecuación (3)
Resolvemos las operaciones y simplificamos:
La solución del sistema es (2,3).
Paso 4. Verifiquemos la solución en cada ecuación del sistema original.
En el siguiente vídeo se muestra la explicación de un ejemplo resuelto por el método de sustitución:
Dirección url del vídeo: http://www.youtube.com/watch?v=3FHhPLVUt9o
PREGUNTA: El sistema 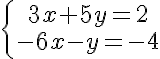 ¿su solución es?
¿su solución es?
Metodo de igualación
Este método consiste en despejar la misma variable en las dos ecuaciones y luego igualarlas.
Apreciemos el trabajo en el siguiente ejemplo:
El siguiente vídeo muestra un ejemplo resuelto:
Fuente:https://www.youtube.com/watch?v=lTRANviJWEY
Método de eliminación.
Para solucionar un sistema de ecuaciones, también podemos adicionar o sustraer las ecuaciones dadas, o sus equivalentes, con el fin de obtener una nueva ecuación con una sola incógnita.
Los pasos para resolver sistemas de ecuaciones por medio del método de la adición o sustracción son:
Paso 1: Adicionar o sustraer miembro a miembro las ecuaciones, para eliminar una incógnita.
Paso 2: Solucionar la ecuación resultante.
Paso 3: Sustituir el valor obtenido en el paso anterior, en cualquiera de las ecuaciones originales, para hallar el valor de la otra incógnita.
Paso 4: Verificar los valores obtenidos en las ecuaciones originales.
Ejemplo: Resolvamos el sistema  , por el método de adición o sustracción.
, por el método de adición o sustracción.
Paso 1. Multiplicamos la ecuación (1) por el coeficiente de la incógnita x, de la ecuación (2), que es 3, y multiplicamos la ecuación (2) por el coeficiente de la incógnita x, de la ecuación (1), que es 5. | |
Paso 2. Restamos, miembro a miembro, las dos ecuaciones obtenidas. | |
Paso 3. Solucionamos la ecuación obtenida | |
Paso 4. Sustituimos a y por -2 en cualquiera de las ecuaciones originales. | |
También habríamos podido multiplicar las ecuaciones por los coeficientes de la incógnita y. | |
Paso 5. Verificamos los valores para x “y” y en las ecuaciones originales. | |
Luego la solución del sistema es (2,-2).
Ejemplo 2:
Adicionamos, miembro a miembro, los términos de las dos ecuaciones. El término en y se ha eliminado . | |
Se soluciona la ecuación resultante |
Sustituimos el valor 4 para x, en cualquiera de las ecuaciones originales, para obtener el valor de y.
En este caso hemos elegido la ecuación (1) para sustituir el valor |
Ahora verificamos si los valores x = 4 “y” y = -3 hacen verdaderas las ecuaciones dadas:
Por tanto, (4,-3) es la solución del sistema.
En el siguiente vídeo se explica un ejemplo por medio del método de eliminación:
Dirección url del vídeo: http://www.youtube.com/watch?v=v6iKv3QXqNs
Sistemas de tres ecuaciones con tres incógnitas
En ocasiones se necesitan más de dos incógnitas para poder expresar, en el lenguaje algebraico, situaciones de la vida real. Analicemos el siguiente problema.
Para resolver sistemas de tres ecuaciones, debemos convertirlo en un sistema de dos ecuaciones con dos incógnitas, por lo cual, se sigue el siguiente procedimiento del ejemplo:
Ejemplo 1: Resolver el sistema: 
Para convertirlo en un sistema de dos ecuaciones con dos incógnitas se sigue el siguiente procedimiento:
1) Multiplicamos por 2 la primera ecuación y la sumamos a la segunda, eliminando z:
2) Multiplicamos por  la tercera ecuación y la sumamos a la primera, eliminando de nuevo z:
la tercera ecuación y la sumamos a la primera, eliminando de nuevo z:
3) Reunimos las ecuaciones resultantes y nos queda un sistema de dos ecuaciones con dos incógnitas:
Este sistema puede ser resuelto por cualquiera de los métodos anteriores. Utilizando sustitución, tenemos:
Sustituyendo en la segunda ecuación
Sustituyendo en la otra ecuación:
Sustituyendo en la segunda ecuación obtenemos el valor de  :
:
4) Por ultimo, sustituyendo los valores de  y
y  en la primera ecuación del sistema de partida, obtenemos el valor de z
en la primera ecuación del sistema de partida, obtenemos el valor de z
La solución definitiva del sistema es, por tanto 
Ejemplo 2: Resolver el sistema: 
Multiplicando la ecuación (1) por 4, la ecuación (2) por -5 y la ecuación (3) por -2, nos resultan las siguientes ecuaciones:
Si sumamos las ecuaciones (4) y (5) y también las ecuaciones (2) y (6), se elimina la incógnita x; veamos:
Sumando las ecuaciones (7) y (8) se elimina la incógnita w:
Remplazando el valor 400 para y en la ecuación (8) tenemos:
Remplazando los valores de y “y” de w en alguna de las ecuaciones originales, por ejemplo en la ecuación (3), podemos hallar el valor de x.
Resolviendo las operaciones obtenemos el valor de x
Verá en el siguiente vídeo un ejemplo práctico, para comprender mejor la lección:
Fuente del vídeo: https://www.youtube.com/watch?v=2S9IJbQIqaE
A) x=1;, y=-1;, z=2
B) x=1;, y=1;, z=-2 C) x=-1;,
y=1;, z=2 D) x=1;, y=1;, z=2
Matrices
Una matriz es un arreglo rectangular de números en filas y columnas, encerrado en un par de paréntesis redondos o cuadrados.
El conjunto de matrices de m filas y n columnas se denota por Amxn o (aij), y un elemento cualquiera de la misma, que se encuentra en la fila i y en la columna j, por aij.
Un elemento se distingue de otro por la posición que ocupa, es decir, la fila y la columna a la que pertenece.
Para nombrar las matrices usaremos letras mayúsculas.
Son ejemplo de matriz:
Cada elemento de la matriz puede localizarse indicando inicialmente el número de la fila n el cual se halla y luego el número de la columna. Para representar cada elemento usaremos el símbolo 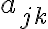 , donde el subíndice
, donde el subíndice 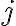 indica el número de la fila y el subíndice
indica el número de la fila y el subíndice  , de la columna. Los números de filas y columnas de una matriz se llaman dimensiones de la matriz. Los encabezamientos de cada fila y columna no forman parte de la matriz.
, de la columna. Los números de filas y columnas de una matriz se llaman dimensiones de la matriz. Los encabezamientos de cada fila y columna no forman parte de la matriz.
Una matriz con 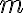 filas y
filas y  columnas tiene dimensiones
columnas tiene dimensiones  .
.
Dos matrices A y B son iguales si tienen las mismas dimensiones y para cada elemento 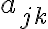 de la matriz A, el elemento correspondiente
de la matriz A, el elemento correspondiente  de la matriz B es exactamente el mismo.
de la matriz B es exactamente el mismo.
PREGUNTA: Las dimensiones de la matriz
Operaciones con matrices
Si dos matrices 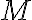 y
y  tienen las mismas dimensiones, la suma de ellas es la matriz
tienen las mismas dimensiones, la suma de ellas es la matriz  , en la cual cada elemento es la suma de los elementos correspondientes de las matrices
, en la cual cada elemento es la suma de los elementos correspondientes de las matrices 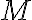 y
y  .
.
Ejemplo:
Es importante tener en cuenta que la adición entre matrices sólo puede efectuarse cuando estas son del mismo tamaño. La suma obtenida es una matriz con las mismas dimensiones de las matrices iniciales.
Si dos matrices 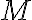 y
y  tienen las mismas dimensiones, entonces la diferencia de ella es la matriz
tienen las mismas dimensiones, entonces la diferencia de ella es la matriz  , en la cual cada elemento es la diferencia entre los elementos correspondientes.
, en la cual cada elemento es la diferencia entre los elementos correspondientes.
Ejemplo:
Hallar la diferencia entre las matrices 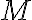 y
y  .
.
Aplicando la definicióin anterior obtenemos la matriz  .
.
PREGUNTA: Sean las matrices E y A como sigue:
![E=\[\begin{array}{ccc}\sqrt{2} & -\frac{5}{3} & 5\\ 9 & 17 & -1\end{array}\] E=\[\begin{array}{ccc}\sqrt{2} & -\frac{5}{3} & 5\\ 9 & 17 & -1\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/755f6a23ef5d424661dd3f4d873656b4.gif)
![A=\[\begin{array}{cc}\sqrt{2} & -\frac{5}{3} \\ 5 & 17\\9 & -1\end{array}\] A=\[\begin{array}{cc}\sqrt{2} & -\frac{5}{3} \\ 5 & 17\\9 & -1\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/41bda41754e2d38ddc6c7bd6615900fd.gif) ¿Es posible sumar las matrices E y A?
¿Es posible sumar las matrices E y A?
Matrices y sistemas de ecuaciones lineales
Existe una relación muy estrecha entre las matrices y los sistemas. Examinemos el siguiente ejemplo, en el cual resolveremos un sistema con dos ecuaciones lineales por medio de matrices.
Ejemplo:
Resolvamos el sistema 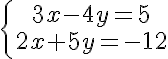 utilizando matrices.
utilizando matrices.
Expresemos el sistema como una matriz. Los elementos que se hallan antes de la línea punteada, son los coeficientes de las incógnitas y los elementos que están después de la línea, son los términos independientes.
Notemos que en el proceso, si mantenemos la posición de la variable  siempre a la izquierda de
siempre a la izquierda de  , podemos prescindir de las letras y de los símbolos
, podemos prescindir de las letras y de los símbolos  , ya que lo impotante son los coeficientes. de esta forma podemos usar lo que se llama la matriz aumentada del sistema para resolverlo, efectuando las correspondientes operaciones que se hicieron con las ecuaciones en las filas de la matriz.
, ya que lo impotante son los coeficientes. de esta forma podemos usar lo que se llama la matriz aumentada del sistema para resolverlo, efectuando las correspondientes operaciones que se hicieron con las ecuaciones en las filas de la matriz.
Dado el sistema de ecuaciones lineales:
La matriz
![\[\begin{array}{cc}a & b\\c & d\end{array}\] \[\begin{array}{cc}a & b\\c & d\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/090d13d5ab3f03e4a8feb2c79ffe7839.gif) se llama matriz de coeficientes del sistema.
se llama matriz de coeficientes del sistema.
Y la matriz se llama matriz aumentada del sistema.
Para el sistema anterior, la matriz de coeficiente es
y la matriz aumentada es .
Después de formar la matriz aumentada de un sistema podemos trabajar con las filas de esta, usando las siguientes trasformaciones, para obtener, en cada paso, una matriz más sencilla, de un sistema equivalente al original.
Pasos para trasformar filas en una matriz
- Intercambiamos dos filas
- Multiplicamos una fila por un número real diferente de cero y adicionamos cada elemento de dicha fila al elemento correspondiente de otra fila.
Para facilitar la explicación de cada paso, usaremos  para denotar la fila
para denotar la fila  . Así,
. Así,  significa que hemos multiplicado la fila 1 por 2,
significa que hemos multiplicado la fila 1 por 2,  significa que hemos multiplicado la fila 2 por -3 y hemos adicionado los correspondientes elementos de la fila 1 con los productos obtenidos de la fila 2, y
significa que hemos multiplicado la fila 2 por -3 y hemos adicionado los correspondientes elementos de la fila 1 con los productos obtenidos de la fila 2, y  indica que se han intercambiado las filas 1 y 2.
indica que se han intercambiado las filas 1 y 2.
El método que usaremos para hallar la solución, si existe, de un sistema de ecuaciones lineales se resume a continuación.
Ejemplo:
Resolvamos el siguiente sistema de ecuaciones:
PREGUNTA: Las matriz aumentada  ¿cual es la solución del sistema?
¿cual es la solución del sistema?
Función
Una función de f de un conjunto A en un conjunto B es una correspondencia que asigna a cada elemento  de A un único elemento y de B.
de A un único elemento y de B.
Frecuentemente en la vida nos encontramos con la noción de correspondencia;por ejemplo, para cada instante de tiempo hay un valor en horas, minutos y segundos.
En la siguiente figura encontramos un ejemplo de correspondencia entre los conjuntos A y B.
Mediante la regla f, se le hace corresponder a cada alumno del conjunto A, su respectivo grado en el conjunto B. Es decir Juan alumno de Noveno, María es alumna de Séptimo y Andrés esta en le grado Once.
El ejemplo anterior de correspondencia determina una función.
El conjunto A se denomina dominio de la función y representa los valores que puede tomar la variable independiente.
El conjunto B se denomina codominio de la función. Algunos o todos sus elementos son imágenes de la función f y se denotan f(x).
Los valores f(X) se denominan rango de la función y representan la variable dependiente.
Una función se puede representar de diferentes formas
- Por medio de una expresión como f(x) = 2x - 1
- Elaborando una tabla de valores como las siguientes
x | 3 | 1 | 5 |
y | 5 | 1 | 9 |
- Con un conjunto de pares ordenados
- Mediante un conjunto nombrado por comprensión.
Pendiente de una recta
Se determinará el valor de la pendiente de una recta.
En matemáticas y ciencias aplicadas se denomina pendiente a la inclinación de un elemento ideal, natural o constructivo respecto de la horizontal.
Una función afín tiene la forma
y su gráfica es una línea recta, donde m es la pendiente y b es la ordenada del punto de intersección entre la recta y el eje Y.
Si b = 0, la función es lineal.
Lineal viene de Línea, de manera que una función lineal, es gráficamente una linea.
Sea l una recta no paralela al eje Y, y P(x1, y1), P2(x2, y2) dos puntos diferentes sobre la recta l.
La pendiente m de l se define por :
El numerador  en la ecuación que define a m, mide el cambio en la dirección vertical al pasar
en la ecuación que define a m, mide el cambio en la dirección vertical al pasar  ; puede ser negativo, positivo o cero.
; puede ser negativo, positivo o cero.
El denominador  mide le camio horizontal al ir de
mide le camio horizontal al ir de  . El denominador puede ser positivo o negativo pero nunca cero, debido a que
. El denominador puede ser positivo o negativo pero nunca cero, debido a que  no es paralela a Y.
no es paralela a Y.
En la siguiente tabla, tenemos la interpretación geométrica de la pendiente de la recta  .
.
Notemos que si la recta 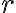 es paralela al eje x, la pendiente es cero. Si la recta
es paralela al eje x, la pendiente es cero. Si la recta  es paralela al eje y, su pendiente no esta definida.
es paralela al eje y, su pendiente no esta definida.
Ejemplo:
Calculemos la pendiente de la recta que pasa por los puntos (6,8) y (2,3).
Solución:
Si nombramos al punto (2,3) como  y al punto (6,8) como
y al punto (6,8) como 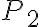 , tenemos que
, tenemos que 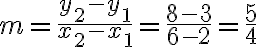 . Como la pendiente es positiva, este ejemplo ilustra el caso 1 de la tabla.
. Como la pendiente es positiva, este ejemplo ilustra el caso 1 de la tabla.
Ejemplo 2:
Solución:
Como la ecuación  no está en la forma explícita, debemos despejar a
no está en la forma explícita, debemos despejar a  antes de señalar la pendiente.
antes de señalar la pendiente.
La ecuación  equivale a
equivale a 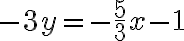 , de donde
, de donde  .
.
Luego  . Ahora sí podemos decir que la pendiente de
. Ahora sí podemos decir que la pendiente de  es
es 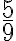
PREGUNTA: ¿Cuál es la pendiente de la recta que pasa por los puntos: (-2,7) y (3,-3)?
Ecuación de una recta que pasa por dos puntos
Por geometría sabemos que dos puntos determinan una recta y que dos o más puntos son colineales si pertenecen a una misma recta.
Puntos Colineales:
Dos o más puntos son colineales si existe una sola recta que los contenga.
A una recta se le puede hacer corresponder una ecuación, si conocemos dos puntos y su pendiente.
Por un punto P1(x1,y1) pasa solamente una recta l con pendiente m. para encontrar la ecuación de la recta l supongammos que P (x,y) es cualquier punto con x ≠ x1, entonces por definición de pendiente tenemos:
La ecuación de la recta en la forma punto-pendiente es:
Ejemplo:
Hallemos la ecuación de la recta que pasa por los puntos A (1,5) y B (-2,2).
Primero debemos encontrar el valor de la pendiente
La pendiente de la recta está determinada por: 
Ahora en la ecuación punto-pendiente podemos sustituir las coordenadas del punto A o del punto B para determinar la ecuación de la recta:
Otra manera de expresar la ecuación de la recta es 
Sabemos que geometricamente dos o más rectas pueden ser secantes o paralelas, esta clasificación se relaciona con las propiedades de las respectivas pendientes.
Rectas Paralelas: dos rectas son geométricamente paralelas, los ángulos respecto al eje x tienen la misma medida.
Dos rectas cualesquiera  son paralela si y sólo si tienen la misma pendiente.
son paralela si y sólo si tienen la misma pendiente.
Rectas Secantes: Si dos rectas no son paralelas, se denominan secantes y se cortan en un solo punto.
Dos rectas secantes son perpendiculares si al cortarse forman un ángulo recto.
Dos rectas cualesquiera l1 y l2 son perpendiculares si y sólo si el producto de sus pendientes es igual a -1.
Ejemplo:
analicemos el producto de las pendientes de las rectas  y
y 
Es conveniente primero despejar a y en cada recta
Consideremos la pendiente de cada recta
Hallemos el producto: 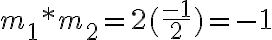 . Las dos rectas son perpendiculares porque el producto de sus pendientes es igual a
. Las dos rectas son perpendiculares porque el producto de sus pendientes es igual a  .
.
PREGUNTA: ¿Cuándo dos rectas son perpendiculares?
Funciones crecientes, decrecientes y constantes.
El valor de la pendiente de una recta nos permite clasificar las funciones lineales y afines, en crecientes, decrecientes y constantes.
la ecuación y = 4 + 2x representa una función afín, cuya gráfica es una línea recta. Para trazar la gráfica hemos construido la siguiente tabla de valores de la ecuación.
X | Y | (X, Y) |
0 | 4 + 2 (0) = 4 | (0,4) |
2 | 4 + 2 (2) = 8 | (2,8) |
5 | 4 + 2 (5) = 14 | (5,14) |
6 | 4 + 2 (6) = 16 | (6,16) |
Observamos que la recta corta el eje Y en el punto (0,4)
Se dice que la intersección con y (y-intersecto) es 4.
Observamos que al aumentar el valor de x, también aumenta el valor de y. En este caso la pendiente es positiva, por tanto, se dice que la función es creciente.
Cuando la pendiente de una recta es positiva, la función lineal o afín a la cual representa, es creciente.
Para las funciones de la forma y = mx + b con m < 0 podemos inferir que:
- Su gráfica es una línea recta.
- su pendiente m es negativa
- son funciones decrecientes constantes.
En general podemos afirmar que las funciones lineales y afínes son funciones de crecimiento o decrecimiento constante.
Cuando el valor de la pendiente de una recta es negativo, la función es decreciente.
Cuando el valor de la pendiente de una recta es cero, la funcón es constante.
Trazado de gráficas de la forma y=mx+b
Hay varias formas de trazar la gráfica de la función  .
.
- Dibujar el plano cartesiano.
- El valor 3 es la intersección de la recta con el eje y. por tanto, ubicamos el punto (0,3)
- Sabemos que 2 es la pendiente, lo que significa que por cada cambio de unidad a la derecha le corresponde un cambio hacia arriba de 2. Aplicando este criterio al punto (0,3), tenemos que otro punto de la recta es: (0 + 1, 3 + 2) = (1,5)
- Ubicamos este punto en el plano y trazamos la recta.
- Comprobemos que el punto (1,5) satisface la ecuación y = 2x + 3
Remplazando el valor del punto en la ecuación de la recta tenemos:
5 = 2(1) + 3, de donde 5 = 5.
También podemos trazar la recta conociendo sólo dos puntos, porque en este caso se aplica el postulado: dos puntos determinan una recta.
Otra manera de dibujar una gráfica de la función afín o lineal es darle valores a la variable independiente y despejar el correspondiente valor para la variable dependiente, y ponerlos en una tabla de valores.
Por ejemplo:
Realizar la grafica de la siguiente ecuación 
Solución:
X | Y |
-1 | 4 |
0 | 1 |
1 | -2 |
PREGUNTA:  encontrar los valores de
encontrar los valores de  cuando
cuando 
La gráfica de Ax+By=C
Recordemos que las ecuaciones traducen al lenguaje algebraico, las condiciones y relaciones que existen entre los datos de un problema.
Situación 1 | Situación 2 |
Supongamos que compramos p pizzas a $ 1500 cada una y b bebidas a $ 500 cada una. La expresión que describe lo que pagamos es 1500p + 500b. | Un químico mezcla x onzas de una solución ácida al 20%, con y onzas de otra solución ácida al 30%. La mezcla final contiene 9 onzas de ácido. La ecuación que describe la situación es: 0.2x + 0.3y = 9. |
Estas expresiones relacionan las variables X y Y mediante una ecuación de la forma Ax + By = C.
Podemos graficar la ecuación de la forma Ax + By = C en el sistema de coordenadas cartesianas, convirtiéndola en una ecuación de la forma y = mx + b, estableciendo explícitamente la pendiente m y el y-intersecto (0,b).
Convirtamos la expresión 0.2x + 0.3y = 9 a la forma y = mx + b, utilizando procedimientos algebraicos:
0.2x + 0.3y = 9
2x + 3y = 90 Multiplicamos por 10 a ambos lados de la igualdad
3y = 90 – 2x Adicionamos -2x a ambos lados.
y = - + 30 Dividimos por 3 a ambos lados.
+ 30 Dividimos por 3 a ambos lados.
La ecuación 0.2x + 0.3y = 9 es equivalente
Tiene pendiente igual a 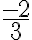 y el intersecto con el eje Y es 30. Podemos afirmar que es una función afín cuya gráfica es una recta decreciente, como se ve en la figura.
y el intersecto con el eje Y es 30. Podemos afirmar que es una función afín cuya gráfica es una recta decreciente, como se ve en la figura.
Expresar una ecuación afín en la forma y = mx + b tiene como ventaja que podemos determinar inmediatamente el y-intersecto, es decir, el punto (0,b). En el ejemplo corresponde a (0,30).
El intersecto con el eje X es la pareja (x,0), lo que significa hacer Y=0 y despejar la X en la ecuación.
-30 = 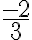 x Adicionamos (-30) a ambos lados de la igualdad.
x Adicionamos (-30) a ambos lados de la igualdad.
-90 = -2x Multiplicamos por 3 a ambos lados
90 = 2x Multiplicamos por (-1) a ambos lados
45 = x Dividimos por 2 a ambos lados.
La intersección de la recta con el eje X es el punto (45,0). Como ya tenemos dos puntos podemos trazar el segmento de recta entre ellos, que se convierte en recta cuando el dominio y el rango son los números reales.
Como conclusión podemos decir:
A una expresión de la forma Ax + By se le llama combinación lineal de X y Y.
A las ecuaciones de la forma Ax + By = C se les denomina "forma estándar de la ecuación lineal con dos variables".
PREGUNTA: ¿Cómo se halla el x-intersecto?
Trazado de gráficas de y=ax² + bx + c
Recordemos que las gráficas con ecuaciones  se denominan parábolas.
se denominan parábolas.
Observemos las siguientes parábolas que tienen las siguientes características.
- Tienen un vértice. Gráfica a) Vértice (0,2); Gráfica b) Vértice (12,2); Gráfica c) Vértice (4,-4).
- Tienen un eje de simetría. La cual es una línea paralela al eje y.
Gráfica a) El eje de simetría es el eje Y; las gráficas b y c, su eje de simetría es la línea de amarillo.
La ecuación de la gráfica c, es de la forma 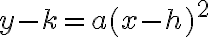 ; esta ecuación es equivalente a la forma
; esta ecuación es equivalente a la forma 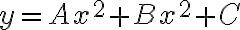 . Veamos porque.
. Veamos porque.
De lo anterior se concluye que:
· Una ecuación de la forma 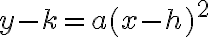 es equivalente a la ecuación
es equivalente a la ecuación  .
.
· La parábola descrita por la ecuación  es congruente con la parábola descrita por la ecuación
es congruente con la parábola descrita por la ecuación  .
.
· En la ecuación  ,
,  es la ordenada del punto de corte de la gráfica con el eje
es la ordenada del punto de corte de la gráfica con el eje  .
.
Si la parábola es cóncava hacia arriba, tiene un mínimo que es el vértice.
Si la parábola es cóncava hacia abajo, tiene un máximo que es el vértice.
Ejemplo:
· Trasformamos la ecuación a 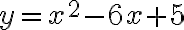 en la forma
en la forma 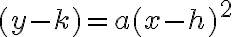
· Debemos expresar  como un trinomio cuadrado perfecto. Para ello apliquemos el procedimiento de completación de cuadrado.
como un trinomio cuadrado perfecto. Para ello apliquemos el procedimiento de completación de cuadrado.
· Recordemos que para completar el cuadrado en una expresión cuadrática de la forma  , se adiciona el cuadrado de la mitad del coeficiente de x; o sea:
, se adiciona el cuadrado de la mitad del coeficiente de x; o sea:  .
.
 | Expresión original |
 | Adicionando el cuadrado de la mitad del coeficiente de  a ambos lados de la igualdad a ambos lados de la igualdad |
 | Simplificando |
 | |
 | Factorizando el trinomio perfecto |
· De esta ecuación determinamos el vértice de la parábola: (3,-4).
· Como a > 0, la parábola es cóncava hacia arriba y tiene un punto mínimo en su vértice.
· Los valores de la tabla, ayudan a definir mejor la gráfica.
Para construir la tabla damos algunos valores a la variable independiente x.
X | Y |
-1 | 12 |
0 | 5 |
1 | 0 |
2 | -3 |
3 | -4 |
4 | -3 |
5 | 0 |
6 | 5 |
7 | 12 |
Solución de ecuaciones cuadráticas
Una función definida de números reales a números reales ( en
en  ), cuyos valores están dados por un polinomio de la forma:
), cuyos valores están dados por un polinomio de la forma:
Toma el nombre de función polinomial de segundo grado o simplemente función cuadrática.
Es conveniente anotar que en  , la variable o incógnita es
, la variable o incógnita es  , el número real
, el número real  es el coeficiente de la variable elevada al cuadrado,
es el coeficiente de la variable elevada al cuadrado,  es el coeficiente de la variable elevada a la potencia
es el coeficiente de la variable elevada a la potencia 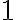 , y
, y  es un término constante o independiente.
es un término constante o independiente.
Formas de la función cuadrática
De acuerdo con la definición de función cuadrática, esta puede tener uno, dos o tres términos. Lo anterior quiere decir que existen forma incompletas y una forma completa, teniendo en cuenta el número de términos; luego se puede clasificar la función cuadrática así:
Formas incompletas:
Ejemplos:
Ejemplos:
Ejemplos:
Forma completa:
Ejemplos:
Ya hemos visto que no importa que valor acompaña la x ya que puede ser 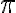 o cualquier otro número real, lo importante para poder indentificar un función cuadrática es ver que el maximo valor del exponente de la x es 2.
o cualquier otro número real, lo importante para poder indentificar un función cuadrática es ver que el maximo valor del exponente de la x es 2.
Ejemplos practicos:
Hallemos la solución de las ecuaciones
Solución:
(raiz en ambos lados de ecuación)
(recordemos que cuando sacamos una raiz cuadrada siempre va
)
La solución es {-8,8}
Ejemplo 2:
Un cuadrado tiene de lado 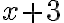 y su área es
y su área es  ; hallemos el valor de
; hallemos el valor de  .
.
Solución:
La solución de la ecuación es 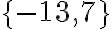 .
.
Podemos verificar.
Sin embargo la solución del problema es sólo 7, ya que  representa una longitud.
representa una longitud.
Expresiones como 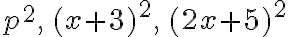 , se denominan cuadrados perfectos.
, se denominan cuadrados perfectos.
Para que una ecuación cuadrática de la forma  tenga solución en el conjunto de los números reales, se requiere que
tenga solución en el conjunto de los números reales, se requiere que 
Ejemplo: Solucionemos la ecuación: 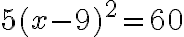
Sacamos raíz cuadrada a ambos lados | |
Descomponemos a 12 en factores primos y extraemos la raíz cuadrada. | |
Adicionamos 9 a ambos lados. |
La solución es  la cual puede verificarse.
la cual puede verificarse.
Veamos:
La ecuación no tiene solución, porque ningún número real, elevado al cuadrado, da como resultado  .
.
No toda ecuación cuadrática tiene la forma  , pero se puede trasformar y llevar a dicha forma, por medio del método llamado completación del cuadrado.
, pero se puede trasformar y llevar a dicha forma, por medio del método llamado completación del cuadrado.
Recordemos el resultado que se obtiene al desarrollar el cuadrado de un binomio:
En cada caso, el coeficiente de  es
es  y el término constante corresponde al cuadrado de la mitad del coeficiente de
y el término constante corresponde al cuadrado de la mitad del coeficiente de  .
.
Método de completación del cuadrado.
Si tenemos la expresión 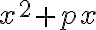 , observamos que hace falta el término constante para que corresponda al desarrollo del cuadrado de un binomio.
, observamos que hace falta el término constante para que corresponda al desarrollo del cuadrado de un binomio.
Entonces la expresión dada podemos trasformarla.
Paso 1. Hallemos la mitad del coeficiente de 
Paso 2. Obtengamos el cuadrado del resultado hallado en el paso anterior:
Paso 3. Adicionemos la expresión obtenida en el paso 2 a la expresión 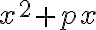 y factoricemos:
y factoricemos:
TENER EN CUENTA: EN UNA ECUACIÓNDE LA FORMA
EL TERMINO
Ejemplo:
Completemos el cuadrado en:
Solución:
Ejemplo:
Solución:
Fórmula cuadrática
FÓRMULA CUADRÁTICA
Toda expresión de la forma  es una ecuación de segundo grado con una incógnita. Los coeficientes
es una ecuación de segundo grado con una incógnita. Los coeficientes  ,
,  y
y  son números reales, positivos o negativos. Se requiere que
son números reales, positivos o negativos. Se requiere que  sea diferente de cero para que la ecuación sea de segundo grado; los coeficientes
sea diferente de cero para que la ecuación sea de segundo grado; los coeficientes  y
y  pueden ser
pueden ser  .
.
Solucionemos la ecuación cuadrática  completando el cuadrado:
completando el cuadrado:
 | ||
 | Adicionamos – c a ambos lados | |
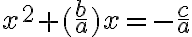 | Dividimos entre  cada término de la ecuación. cada término de la ecuación. | |
 | Completamos el cuadrado adicionando 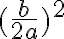 a cada lado. a cada lado. | |
![[x+(\frac{b}{2a})]^2=-\frac{c}{a}+\frac{b^2}{4a^2} [x+(\frac{b}{2a})]^2=-\frac{c}{a}+\frac{b^2}{4a^2}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/ef295206c07e7b4fe8174f51540f546a.gif) | ||
![[x+(\frac{b}{2a})]^2=\frac{-4ac+b^2}{4a^2}=\frac{b^2-4ac}{4a^2} [x+(\frac{b}{2a})]^2=\frac{-4ac+b^2}{4a^2}=\frac{b^2-4ac}{4a^2}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/f45975d7ddb71dd26c64f38b1a66c77d.gif) | ||
 | ||
 | Si  | |
 | ||
La última expresión que indica la solución de la ecuación, se conoce con el nombre de fórmula cuadrática. Esta nos da las raíces de la ecuación cuadrática  en términos de los coeficientes
en términos de los coeficientes  ,
,  y
y  .
.
La ecuación cuadrática  tiene dos soluciones que corresponden a números reales, cuando
tiene dos soluciones que corresponden a números reales, cuando  . Tales soluciones son:
. Tales soluciones son:
Si 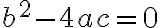 , las dos soluciones coinciden. Se tiene entonces;
, las dos soluciones coinciden. Se tiene entonces;
Si 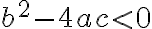 la ecuación cuadrática no tiene solución en el conjunto de los números reales.
la ecuación cuadrática no tiene solución en el conjunto de los números reales.
Como el valor de  discrimina o diferencia el número de raíces de la ecuación cuadrática, se conoce con el nombre de discriminante de
discrimina o diferencia el número de raíces de la ecuación cuadrática, se conoce con el nombre de discriminante de  .
.
Ejemplo 1:
Hallemos la solución de la ecuación 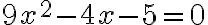
Como  , para los valores dados queda:
, para los valores dados queda:
El conjunto solución de la ecuación es: 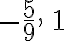
Ejemplo 2:
Solución:
Primero igualamos a cero la ecuación: 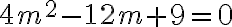
Luego:
El conjunto solución de la ecuación es 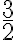 , un solo valor, pues
, un solo valor, pues 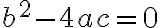
Ejemplo 3:
Solucionar la ecuación 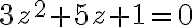 , usando la fórmula cuadrática.
, usando la fórmula cuadrática.
Hemos visto varios métodos para resolver ecuaciones cuadráticas. Resumen de los métodos vistos.
Ejemplo 4:
Aquí podemos usar la fórmula cuadrática, el método de factorización o la completación del cuadrado. Como  es impar, no usamos el último porque es más complicado.
es impar, no usamos el último porque es más complicado.
Solución:
| Formula cuadrática | Factorización |
 | a * c = 6, b = -7 = - 6 + (-1) |
 |  |
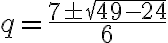 | 3q(q – 2) – 1(q – 2) = 0 |
 | (3q – 1)(q – 2) = 0 |
 | 3q – 1 = 0 o q – 2 = 0 |
 |  |
PREGUNTA: La solución de la ecuación  es:
es:
Gráfica de la función cuadrática
En la unidad  vimos el trazado de gráficas de funciones cuadráticas, ahora estudiaremos cómo los ceros de estas funciones son, a su vez, soluciones de la ecuación cuadrática.
vimos el trazado de gráficas de funciones cuadráticas, ahora estudiaremos cómo los ceros de estas funciones son, a su vez, soluciones de la ecuación cuadrática.
Comencemos por analizar la gráfica de la función  definida por la ecuación
definida por la ecuación 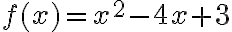
Hagamos una tabla de valores y hallemos las coordenadas de algunos de los puntos de la gráfica de al función: 
Notemos que hay dos valores distintos de  que dan exactamente el mismo valor para
que dan exactamente el mismo valor para  .
.
El único valor de  que no tiene otro valor para
que no tiene otro valor para  , es
, es  . Además como
. Además como  para todo valor de
para todo valor de  , entonces
, entonces  . Eso significa que el valor mínimo para
. Eso significa que el valor mínimo para  es
es  , que se obtiene cuando
, que se obtiene cuando  .
.
Teniendo en cuenta el análisis anterior, podemos hacer un bosquejo de la gráfica, como se muestra en la figura.
La parábola de la función 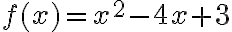 es cóncava hacia arriba porque
es cóncava hacia arriba porque 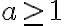 y el punto de coordenadas
y el punto de coordenadas  es el punto mínimo que corresponde al vértice. La recta vertical de ecuación
es el punto mínimo que corresponde al vértice. La recta vertical de ecuación  se llama eje de simetría de la parábola. El punto de coordenadas
se llama eje de simetría de la parábola. El punto de coordenadas  es el y-intersecto y los puntos de coordenadas
es el y-intersecto y los puntos de coordenadas 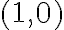 y
y  son los x-intersectos. Notemos que las abscisas de esos puntos, es decir
son los x-intersectos. Notemos que las abscisas de esos puntos, es decir  y
y 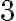 , son las soluciones de las ecuación
, son las soluciones de las ecuación 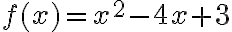 .
.
Como anotamos anteriormente, todos los puntos de una parábola, excepto el vértice, aparecen en pares que tienen la misma ordenada y diferente abscisa; la abscisa en el vértice corresponde al valor medio entre los valores de las abscisas de puntos con igual ordenada.
Si representamos las gráficas de las ecuaciones  en la figura, vemos que todas ellas tienen la misma abscisa en el vértice.
en la figura, vemos que todas ellas tienen la misma abscisa en el vértice.
Las ecuaciones se diferencian |entre sí sólo por el término independiente. Podemos hallar una expresión para la abscisa del vértice de la parábola  . Si en la ecuación
. Si en la ecuación  buscamos los puntos donde la curva corta al eje
buscamos los puntos donde la curva corta al eje  , es decir, los puntos donde la ordenada vale
, es decir, los puntos donde la ordenada vale  , tenemos:
, tenemos:
El valor medio entre los dos valores de x es 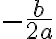 . Por tanto, el valor de la abscisa del vértice de la parábola es
. Por tanto, el valor de la abscisa del vértice de la parábola es 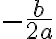 .
.
Remplazando el valor de  en la ecuación de la parábola, podemos hallar la ordenada del vértice.
en la ecuación de la parábola, podemos hallar la ordenada del vértice.
Por tanto, las coordenadas del vértice de una parábola de ecuación  son
son 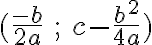
Hemos encontrado dos maneras de hallar las coordenadas del vértice de la parábola, una como aparece en ele desarrollo anterior, y la otra, completando el cuadrado, como se hizo en el primer caso desarrollado en la lección. Cuando se obtiene la expresión de la forma 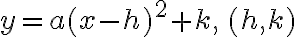 son las coordenadas del vértice.
son las coordenadas del vértice.
La ecuación del eje de simetría de la parábola es 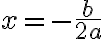 .
.
Ejemplo:
Representemos la curva de ecuación 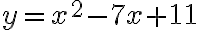 ; hallemos las coordenadas del vértice y de los interfectos con los ejes.
; hallemos las coordenadas del vértice y de los interfectos con los ejes.
Solución:
Interfectos:
El intersecto con el eje  es el punto de coordenadas (0,11).
es el punto de coordenadas (0,11).
Hay dos intersectos con el eje  ,
, 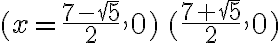 , ya que la ecuación
, ya que la ecuación 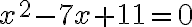 tiene dos raíces reales. La gráfica se muestra en la figura.
tiene dos raíces reales. La gráfica se muestra en la figura.
PREGUNTA: Las coordenadas del vértice de la función 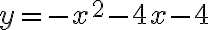 son:
son:
Desigualdades cuadráticas
Hemos aprendido a hacer un modelo de la grafica de funciones de la forma  . Ahora estudiaremos algunos casos de desigualdades cuadráticas. La gráfica de estas desigualdades consta de todos los puntos
. Ahora estudiaremos algunos casos de desigualdades cuadráticas. La gráfica de estas desigualdades consta de todos los puntos  que son solución de la desigualdad.
que son solución de la desigualdad.
Analicemos la gráfica de los puntos que satisfacen la desigualdad  .
.
Los puntos que cumplen la ecuación 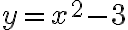 son los de la parábola que abre hacia arriba, cuyo vértice esta en (0,-3) y sus x-intersectos son
son los de la parábola que abre hacia arriba, cuyo vértice esta en (0,-3) y sus x-intersectos son 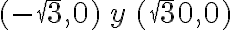 , como se muestra en la figura.
, como se muestra en la figura.
La curva divide el plano entres regiones: los puntos dentro de la curva, los puntos en la curva y los puntos fuera de esta. ¿Cuáles de esos puntos satisfacen la desigualdad?
Por ejemplo, todos los que tienen abcisa  y ordena mayor que
y ordena mayor que 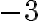 , ya que si
, ya que si 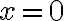 , la desigualdad se trasforma en
, la desigualdad se trasforma en  , por ejemplo (0,1), (0,15), porque
, por ejemplo (0,1), (0,15), porque 
Si analizamos la relación que existe entre la ordenada y la abcisa de los puntos que están sobre la recta  , encontramos que le punto
, encontramos que le punto 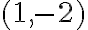 pertenece a la parábola, y todos los puntos
pertenece a la parábola, y todos los puntos  con
con  , son puntos de la región que estamos tratando de determinar. Por ejemplo
, son puntos de la región que estamos tratando de determinar. Por ejemplo  ;
; 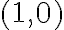 ;
;  , están en la región, porque:
, están en la región, porque:
En resumen, cumplen la desigualdad, todos los puntos del plano que están sobre la parábola por encima de ella. Los puntos que cumplen la desigualdad corresponden a la región sombreada que se muestra en la figura.
Cuando los puntos de la curva pertenecen a la gráfica de la región, se dice que la región es cerrada, si no pertenecen, se dice que la región es abierta.
La gráfica de la región sombreada corresponde a la relación  . El dominio de la relación son los números reales, y el rango son los números reales mayores o iguales que
. El dominio de la relación son los números reales, y el rango son los números reales mayores o iguales que 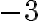 , puesto que
, puesto que 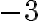 es la ordenada del vértice de la parábola, el punto más bajo de la curva.
es la ordenada del vértice de la parábola, el punto más bajo de la curva.
Ejemplo 1:
Tracemos la gráfica de los puntos del plano que satisfacen la desigualdad 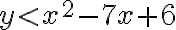
Tracemos primero los puntos de la parábola 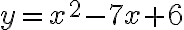 , con línea interrumpida, puesto que esos puntos no satisfacen la desigualdad.
, con línea interrumpida, puesto que esos puntos no satisfacen la desigualdad.
La parábola abre hacia arriba, su vértice es el punto  , el y-intersecto es
, el y-intersecto es 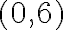 , los x-intersectos son
, los x-intersectos son 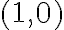 .
.
Ahora localicemos algunos puntos que satisfacen la desigualdad. Si trazamos en el mismo plano donde está la gráfica de la parábola la recta  , el punto
, el punto 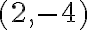 de la recta queda sobre la parábola. Los puntos de abcisa
de la recta queda sobre la parábola. Los puntos de abcisa  y ordenada menor que
y ordenada menor que  , satisfacen la desigualdad dada. Por ejemplo, los puntos de coordenadas
, satisfacen la desigualdad dada. Por ejemplo, los puntos de coordenadas  ,
,  ,
,  , porque:
, porque:
De igual manera los puntos de la recta  cuya coordenada sea menor que
cuya coordenada sea menor que  , satisfacen la desigualdad. Por ejemplo
, satisfacen la desigualdad. Por ejemplo  , ya que
, ya que  . Por tanto, satisfacen la desigualdad todos los puntos del plano que están por debajo de la parábola de la ecuación
. Por tanto, satisfacen la desigualdad todos los puntos del plano que están por debajo de la parábola de la ecuación  . La región sombreada que se muestra en la figura corresponde a la grafica de los puntos que satisfacen la desigualdad.
. La región sombreada que se muestra en la figura corresponde a la grafica de los puntos que satisfacen la desigualdad.
El dominio y el rango de la relación son los números reales.
Ejemplo 2:
Realicemos la gráfica de los puntos del plano que satisfacen simultáneamente las condiciones: 
Primero ubicamos los puntos de la parábola  . Está tiene por vértice a
. Está tiene por vértice a 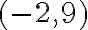 , y-intersecto a (0,5), x-intersectos a (-5,0), (1,0) y abre hacia abajo.
, y-intersecto a (0,5), x-intersectos a (-5,0), (1,0) y abre hacia abajo.
Ahora ubicamos los puntos que satisfacen la primera desigualdad que son, además de los que pertenecen a la parábola, todos los que están por debajo de la parábola. En la grafica correspondiente a la región sombreada con verde.
Posteriormente ubicamos la recta de la ecuación  y, por ultimo, los puntos que satisfacen la desigualdad. En la grafica es la región sombreada con rojo.
y, por ultimo, los puntos que satisfacen la desigualdad. En la grafica es la región sombreada con rojo.
Los puntos del plano que satisfacen simultáneamente las dos condiciones son los que pertenecen a la región que en la gráfica tiene los dos colores, es decir, la intersección entre las regiones determinadas por las desigualdades  , que se muestra en la figura.
, que se muestra en la figura.
Las coordenadas de los puntos de intersección de la parábola y la recta la podemos encontrar resolviendo el sistema.
Remplazando (2) en (1) tenemos:  igualando a cero la ecuación tenemos:
igualando a cero la ecuación tenemos: 
Como la ecuación (2) exige que la ordenada y la abcisa sean iguales, la solución del sistema son los pares 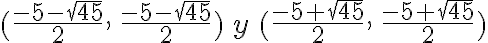
El dominio de la relación que satisface simultáneamente las condiciones dadas es el intervalo ![[\frac{-5-\sqrt{45}}{2},\,\frac{-5+\sqrt{45}}{2}] [\frac{-5-\sqrt{45}}{2},\,\frac{-5+\sqrt{45}}{2}]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/a4645e483c7079a058493b8c9190d114.gif) . El rango de la relación es el intervalo
. El rango de la relación es el intervalo ![[\frac{-5-\sqrt{45}}{2},\,9] [\frac{-5-\sqrt{45}}{2},\,9]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/fc6373ef0ae27628b18814f666d7a8fe.gif) .
.
PREGUNTA: Una desigualdad cuadrática se identifica por que:



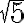


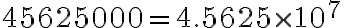




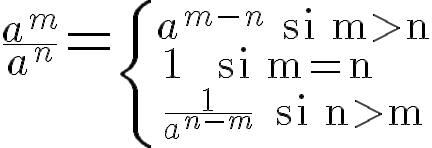

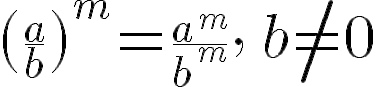


![\Huge \sqrt[n]{x}=x^{\frac{1}{n}},\,\, x\geq 0 \Huge \sqrt[n]{x}=x^{\frac{1}{n}},\,\, x\geq 0](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e70f0f8d6bde65fdc336185becb1b1a7.gif)
![\Huge \sqrt[n]{x^m}=(\sqrt[n]{x})^m=x^{\frac{m}{n} \Huge \sqrt[n]{x^m}=(\sqrt[n]{x})^m=x^{\frac{m}{n}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/8044efb6cc63c30b5a0c9c980674d318.gif)
![\Huge \sqrt[n]{\sqrt[m]{x}}=\sqrt[n*m]{x} \Huge \sqrt[n]{\sqrt[m]{x}}=\sqrt[n*m]{x}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/6321e1eac33a903bc1468f1a75da6043.gif)
![\Huge \sqrt[n]{x*y}=\sqrt[n]{x}*\sqrt[n]{y} \Huge \sqrt[n]{x*y}=\sqrt[n]{x}*\sqrt[n]{y}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/8334e82978906b05af68adfc0a1b452d.gif)
![\Huge \sqrt[n]{\frac{x}{y}}=\frac{\sqrt[n]{x}}{\sqrt[n]{y}},\,\, y\neq 0 \Huge \sqrt[n]{\frac{x}{y}}=\frac{\sqrt[n]{x}}{\sqrt[n]{y}},\,\, y\neq 0](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/1269bdbf2a9f38dbe46b76955c3b4416.gif)
![\Huge \sqrt[n]{a^n}=\mid a \mid \Huge \sqrt[n]{a^n}=\mid a \mid](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/6f57cc009cd04af322290b77be02b969.gif)
![\Huge \sqrt[n]{a^n}=a \Huge \sqrt[n]{a^n}=a](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/4400d7aba6b54b5e8e254d26c1aeacb6.gif)













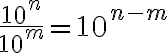





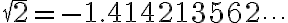
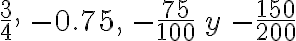

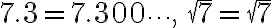

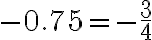
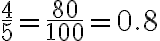

![\Huge \log_a{b} = n\Leftrightarrow a^n = b\Leftrightarrow\sqrt[n]{b} = a \Huge \log_a{b} = n\Leftrightarrow a^n = b\Leftrightarrow\sqrt[n]{b} = a](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b68619db8883a89598c7b030e8dd4f03.gif)
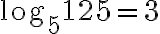







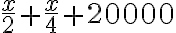






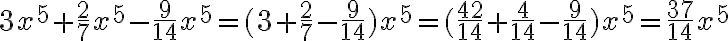



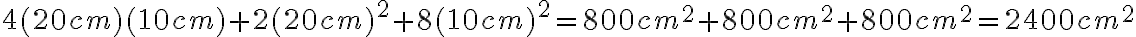



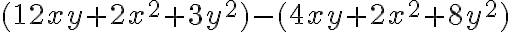
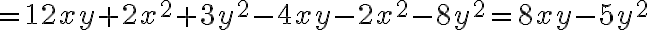



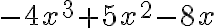

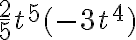


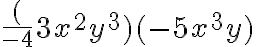



(b^2b^3b^4) =\[(-8))\frac{5}{4})(-\frac{3}{2}](a^2aa^3)(b^2b^3b^4)](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/a2051d0607884083d3d02cbe755e1d48.gif)


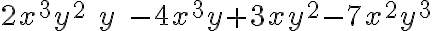
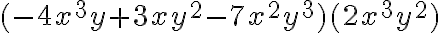

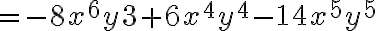

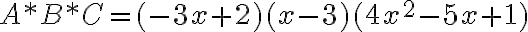

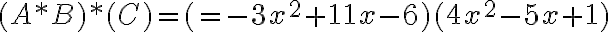

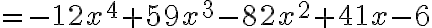






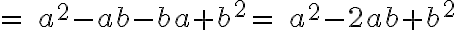


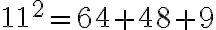

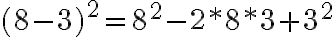


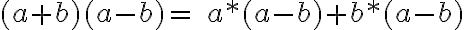
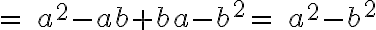

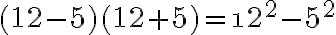

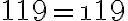
![(a+b)^3=\(a+b) (a+b) (a+b)=\[ (a+b) (a+b)] (a+b) (a+b)^3=\(a+b) (a+b) (a+b)=\[ (a+b) (a+b)] (a+b)](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/3261b6523efc0e7ccc6217e39e90e6cf.gif)




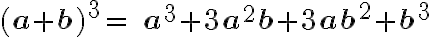


![(a-b)^3=\(a-b) (a-b) (a-b)=[ (a-b) (a-b)] (a-b) (a-b)^3=\(a-b) (a-b) (a-b)=[ (a-b) (a-b)] (a-b)](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/233161211219f9a4a6b9f23c1e711f65.gif)



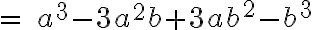

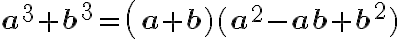



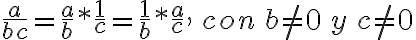

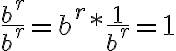
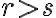
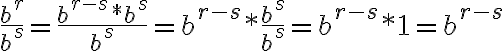


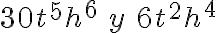
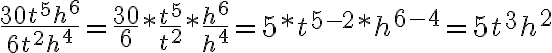
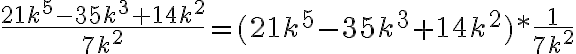
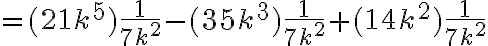


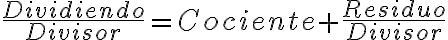





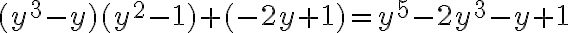
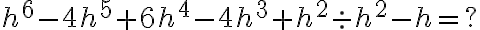

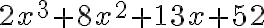




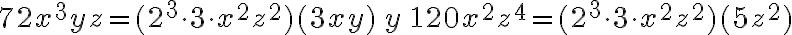


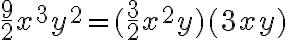

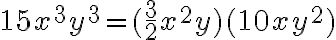
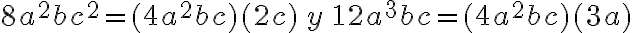




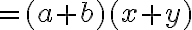
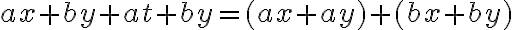

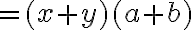

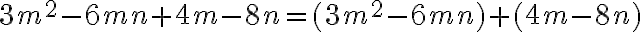
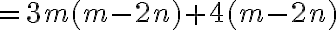



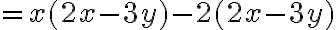
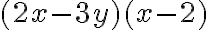



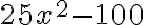
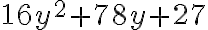
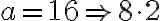
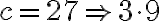
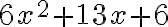

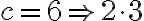

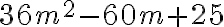



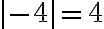


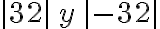

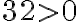
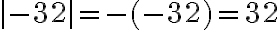



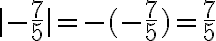
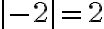


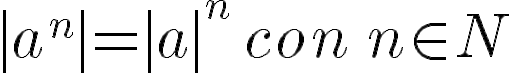
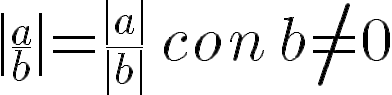







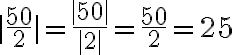




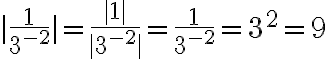







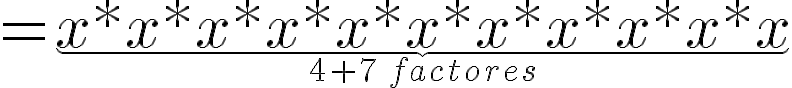

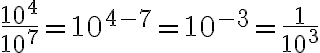

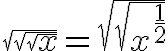
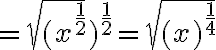

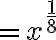
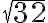

![(\frac{5\sqrt{y}}{125\sqrt[3]{y}})^3 (\frac{5\sqrt{y}}{125\sqrt[3]{y}})^3](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/8f34b44977d45d59585f6adbf851c8e9.gif)
![=\frac{5^3\sqrt{y}^3}{125^3\sqrt[3]{y}^3} =\frac{5^3\sqrt{y}^3}{125^3\sqrt[3]{y}^3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/111983c78202b8c15ccd6f0923ca2766.gif)
![=\frac{125\sqrt{y}\sqrt{y}^2}{125^3\sqrt[3]{y^3} =\frac{125\sqrt{y}\sqrt{y}^2}{125^3\sqrt[3]{y^3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/3feac36354cc2620913ea9de47f19af4.gif)


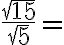
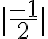
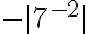
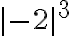
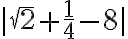
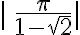
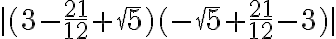
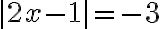
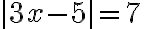
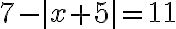
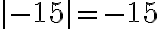
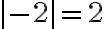
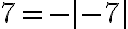
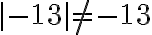
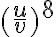
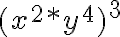
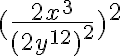
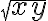
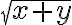
![\sqrt[3]{xy^2} \sqrt[3]{xy^2}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/5ae8960873502369b256475152ad0d0a.gif)
![\sqrt[3]{x^7} \sqrt[3]{x^7}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/2bf748173798842890d451da0ec5f7bd.gif)
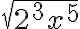
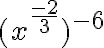
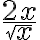
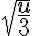
![6\over\Large\sqrt[3]{3} 6\over\Large\sqrt[3]{3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/877c68c416c7a155c42d29c637350b24.gif)
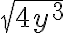
![\sqrt[3]{x^{2}y} \sqrt[3]{x^{2}y}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/dc8a235bfcc978029001caadc95d707f.gif)
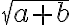
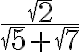
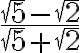

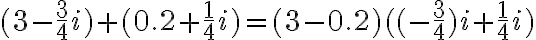



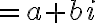

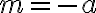
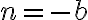


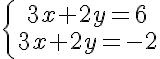

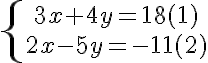



![3[-\frac{11}{2}+\frac{5}{2}y]+4y=18 3[-\frac{11}{2}+\frac{5}{2}y]+4y=18](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/7e1a0d03d623d1349229de650f83d582.gif)
![-\frac{33}{2}+[\frac{15+8}{2}y]=18 -\frac{33}{2}+[\frac{15+8}{2}y]=18](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/8bf675a31d863df69add7a06ad37fb92.gif)


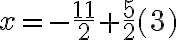
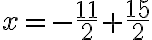
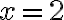





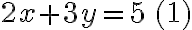


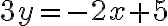





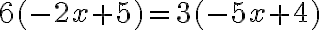

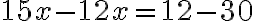

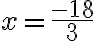





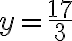

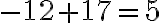
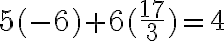


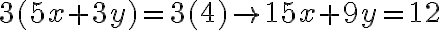


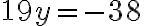

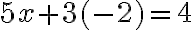


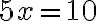

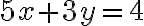





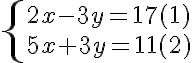

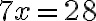
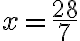
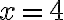




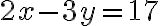
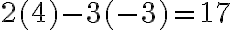


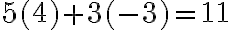

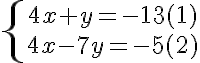

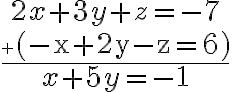



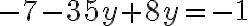

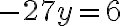
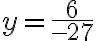








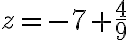


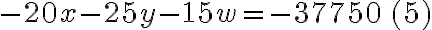

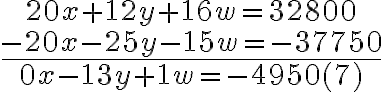
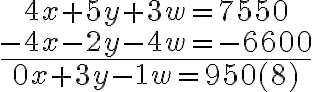




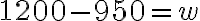
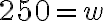






![B=\[\begin{array}{cc}2 & -1\\0 & \frac{3}{2}\end{array}\] B=\[\begin{array}{cc}2 & -1\\0 & \frac{3}{2}\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/296ece75dec39d0db81bdcf942f32835.gif)
![M=\[\begin{array}{cccccc}35 & 25 & 15 & 34 & 17 & 23\\39 & 24 & 5 & 15 & 19 & 12\\24 & 18 & 29 & 12 & 20 & 18\end{array}\] M=\[\begin{array}{cccccc}35 & 25 & 15 & 34 & 17 & 23\\39 & 24 & 5 & 15 & 19 & 12\\24 & 18 & 29 & 12 & 20 & 18\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/5189337cf808c0e251d3bed0aefad59b.gif)
![N=\[\begin{array}{cccccc}45&49&35&29&5&43\\23&30&4&11&2&43\\44&15&17&32&29&18\end{array}\] N=\[\begin{array}{cccccc}45&49&35&29&5&43\\23&30&4&11&2&43\\44&15&17&32&29&18\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/19cbc0ff1a2815d89246e39ce211a840.gif)
![M+N=\[\begin{array}{cccccc}80&74&50&63&22&66\\62&54&9&26&21&18\\68&33&46&44&49&38\end{array}\] M+N=\[\begin{array}{cccccc}80&74&50&63&22&66\\62&54&9&26&21&18\\68&33&46&44&49&38\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/83cb43fbd206a25c4f8c3340f09cb193.gif)
![M-N=\[\begin{array}{cccccc}-10&-24&-20&5&12&-20\\16&-6&1&4&17&6\\-20&3&12&-20&-9&-2\end{array}\] M-N=\[\begin{array}{cccccc}-10&-24&-20&5&12&-20\\16&-6&1&4&17&6\\-20&3&12&-20&-9&-2\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/49b75a494a389bfe299d6901bafc3007.gif)

![\[\begin{array}{cc}3&-4\\2&5\end{array}\] \[\begin{array}{cc}3&-4\\2&5\end{array}\]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/62a884af6a1b60374ffa86ec900eee79.gif)




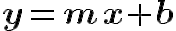


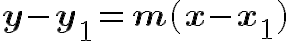




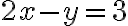

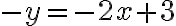
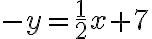
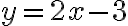



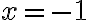


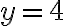
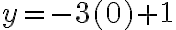











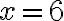




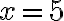

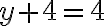
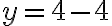



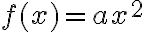
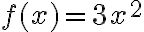


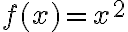

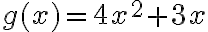



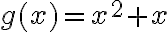


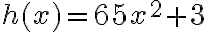





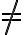

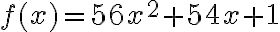


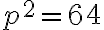


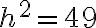


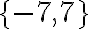


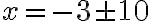












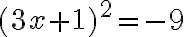




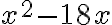

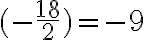

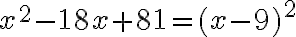






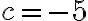
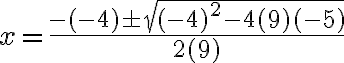


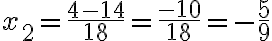
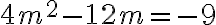
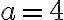

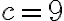

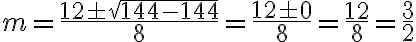






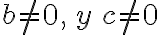
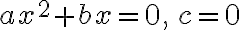


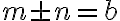




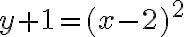










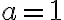

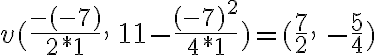


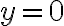





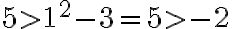







Comentarios
Publicar un comentario