Matematicas 6º y 7º
MAURICIO MUÑOZ MATEMÁTICO FÍSICO UNIVALLE
6° MATEMÁTICAS
Origen
Para contar, el hombre hacia correspondencias asociando a cada objeto observado una marca o signo que le fuera familiar, de esta forma lograba hacer distinción entre una unidad y muchas unidades
Inicialmente el hombre realizaba correspondencias entre partes de su cuerpo y lo que estaba contando. Por ejemplo, para referirse a un grupo de cuatro, cinco o seis animales, podía decir simplemente que era una "mano" de animales; entonces todos entendían lo que eso significaba: que había, más o menos, tantos animales como dedos hay en la mano. Esta clase de asociación entre partes del cuerpo y objetos, condujo al hombre a trabajar con distintas agrupaciones
Algunos usaron los dedos de las manos; de este modo, contaron de diez en diez; otros utilizaron los dedos de las manos y los pies. para contar de veinte en veinte.
Números naturales
Un sistema de numeración es una colección de símbolos junto a unas reglas de formación de nuevos símbolos, los cuales nos sirven para representar números
Los números naturales son aquellos que normalmente utilizamos para contar. Son aquellos números positivos y sin parte decimal.
El conjunto de los números naturales tiene las siguientes propiedades:
• Es utilizado para contar los elementos de un conjunto.• El proceso de enumeración de sus elementos no termina, por lo tanto es un conjunto infinito.• Dado un número natural cualquiera, se sabe con seguridad qué natural sigue, por lo tanto es ORDENADO.
Dados dos números naturales cualesquiera a, b puede suceder alguna de las siguientes relaciones:
a es igual a b y se indica a= ba es menor que b y se indica a < ba es menor que o igual a b y se indica aba es mayor que b y se indica a > ba es mayor que o igual a b y se indica a
b
PREGUNTA: Seleccione la lista de números naturales
10, 895, 301, -7 -2, 35, 97, 100, 6, 4, 1000, 2
VALOR POSICIONAL
Todo los números están formados por dígitos o cifras que pueden repetirse dentro del mismo número, los cuales pueden ser:

Ejemplos:424 (cuatrocientos veinticuatro)325 (trescientos veinticinco)2250 (dos mil doscientos cincuenta)
Ejemplo practico:
Observemos el aviso clasificado.
¿Cuál es el menor?
Pese a que sólo se usaron dos dígitos para formar los diferentes números que aparecen en el aviso, la posición que ocupa el 6 en cada uno de ellos hace que represente cantidades distintas. Por ejemplo, el apartamento se separa con seiscientos mil pesos, pero la cuota inicial es seis millones de pesos. Aun cuando el seis se desplazó sólo una posición a la izquierda, la cantidad aumentó diez veces.
La figura que aparece a continuación muestra los nombres de las distintas posiciones que puede ocupar un dígito.
En la anterior figura la posición del dígito 6 en el numeral que expresa el área del apartamento es la de las decenas, mientras que en el numeral que expresa el valor de la cuota inicial, el 6 está en la posición de las unidades de millón.
Por ejemplo el numeral 555 utiliza el dígito 5 en tres posiciones diferentes
Cada vez que un dígito se desplaza un lugar hacia la izquierda aumenta diez veces su valor.
El sistema que usamos para contar lo llamamos decimal ya que los números se van repitiendo de 10 en 10.
Ejemplos:0,1,2,3,...,10, 11,...,19,20,21,22,...,29,30,31,...
PREGUNTA: El sistema decimal es:
A ) Posiciona B) No posicional
3 Lección: Bases numéricas
BASES NUMÉRICAS
En la unidad anterior vimos que el sistema en que trabajamos tiene diez dígitos, (0,1,2,3,4,5,6,7,8 y 9) pero en algunas ocasiones se trabaja con menos dígitos, por ejemplo en computación el cual trabaja con solo ceros y unos. Cuando se hacen grupos de cierto número de elementos para contar, ese número se llama base.
Sistema Numérico: Se llama sistema numérico al conjunto ordenado de símbolos o dígitos y a las reglas con que se combinan para representar cantidades numéricas.
Existen diferentes sistemas numéricos, cada uno de ellos se identifica por su base.
Dígito: Un dígito en un sistema numérico es un símbolo que no es combinación de otros y que representa un entero positivo.
Base de un sistema numérico: La base de un sistema numérico es el número de dígitos diferentes usados en ese sistema.
A continuación se ejemplifican estas definiciones con los sistemas numéricos más comúnmente usados que son:
Decimal, utiliza 10 símbolos (dígitos) : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Binario, utiliza 2 símbolos (dígitos) : 0, 1
Octal, utiliza 8 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7
Hexadecimal, utiliza 16 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
U otros con cualquier base:
Terciario (Base 3), utiliza 3 símbolos (dígitos): 0, 1, 2
Cuaternario (Base 4), utiliza 4 símbolos (dígitos): 0, 1, 2, 3
Quinario (Base 5), utiliza 5 símbolos (dígitos): 0, 1, 2, 3, 4
Senario (Base 6), utiliza 6 símbolos (dígitos): 0, 1, 2, 3, 4, 5
Heptal (Base 7), utiliza 7 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6
Nonario (Base 9), utiliza 9 símbolos (dígitos): 0, 1, 2, 3, 4, 5, 6, 7, 8
etc.
Notación: Para distinguir entre los diferentes sistemas numéricos se puede encerrar entre paréntesis el número y se le añade un subíndice que indicará la base que se está usando.
Sin embargo, si no se usa subíndice se deberá entender que el número está en base diez, a menos que se diga lo contrario.
Ejemplos:
La siguiente tabla muestra las equivalencia entre los diferentes sistemas de numeración.
Fuente: https://www.youtube.com/watch?v=X-l63IUCXvA
Vemos en la tabla que a medida que aumenta la base la extensión de número es más corta, por ejemplo  en base
en base 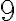 es mas corto que su equivalente en base
es mas corto que su equivalente en base 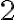
 .
.
PREGUNTA: ¿Cual sería el valor de  en base
en base 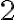 ,
,  y
y 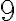 ?
?
A) 1100101, 60, 50 B) 110010, 62, 55 C) 1100011, 63, 58
4 Lección: Números Romanos
NÚMEROS ROMANOS
Los orígenes de la civilización romana se remontan al siglo VIII antes de cristo.
Su dominio del mundo fue tan extenso y por tantos siglos, que no sorprende que aún usemos su sistema de numeración.
Los Romanos Utilizaron siete letras para representar sus numerales
Reglas para la escritura de los números
- Las letras I,X,C y M pueden repetirse hasta 3 veces
- Las letras V,L,D, no se anteponen ni se repiten
- Una letra colocada a la derecha de una de mayor valor, significa que su valor debe sumarse
- Una letra colocada a la izquierda de una de mayor valor, significa que su valor debe restarse
- Si a una letra se le coloca una línea horizontal encima significa que su valor se multiplica por 1000
Ejemplo:
El número 999 se escribe CMXCIX
Haga clic en el siguiente vínculo para realizar una actividad interactiva con números romanos
PREGUNTA: ¿Cómo se escribe el número 885 en numeración romana?
A) DCCCLXXXV B) DCCCCVC C) DCCMLXXXV
ADICIÓN DE NÚMEROS NATURALES
La adición de dos o más números naturales cualquiera a y b se simboliza así: a+b=c. Los elementos de la adición son los sumandos a y b, el resultado es c.
La adición entre números naturales cumple las siguientes propiedades.
La operación inversa de la adición de números naturales es la SUSTRACCIÓN , luego si a + b = c , entonces c - a = b . Al número natural c se llama MINUENDO , al natural a SUSTRAENDO y al natural b DIFERENCIA .
Ejemplo:
| 5 | - | 3 | = | 2 |
| Minuendo | Menos | Sustraendo | Igual | Diferencia |
PREGUNTA: 2 + 3 = 3 + 2 =5 ¿Qué propiedad se utilizo?
Asociativa Conmutativa Clausurativa Modulativa
Situaciones de multiplicación y división
MULTIPLICACIÓN
La operación, que es una suma abreviada de sumandos iguales, se llama MULTIPLICACIÓN. La multiplicación entre dos números naturales a y b, se simboliza así:
El punto y el signo x indican multiplicación. Cada término que interviene en la operación se llama FACTOR. El número que se repite se llama MULTIPLICANDO y el número de veces que el sumando se repite se llama MULTIPLICADOR.
Ejemplo: 3 veces 5 = 15 esto significa 5 + 5 + 5 = 15
PROPIEDADES DE LA MULTIPLICACIÓN
DIVISIÓN
La operación inversa respecto a la multiplicación se llama DIVISIÓN. Si se conoce el producto de dos factores y uno de esos mismos factores, se puede hallar por medio de la división el otro factor. El signo de la división es 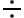
Simbólicamente: Si a, b, c son números naturales tales que:
En una división exacta los términos son: dividendo, divisor, cociente.
Cuando un número divide a otro exactamente, se dice: éste es divisible por él.
Ejemplo: 15 es divisible por 3, por que 
PREGUNTA: ¿Qué propiedad se utilizo?
(2 x 3) x 2 = 2 x (3 x 2)
6 x 2 = 2 x 6
12 = 12
a) Distributiva respecto a la adición c) Distributiva respecto a la sustracción
b) conmutativa d)Asociativa
7 Lección: Potenciación
POTENCIACIÓN
Sabemos que elevar un número cualquiera a una potencia es multiplicar dicho número por si mismo tantas veces como indique el exponente, es decir:
Ejemplos:
1.
Donde el 2 es la base, el número 8 es el exponente, y el número 256 es la potencia.
Lo que quiere decir que el número dos, multiplicado por si mismo ocho veces nos da 256
así.
2 x 2 = 4
4 x 2 = 8
8 x 2 = 16
16 x 2 = 32
32 x 2 = 64
64 x 2 = 128
128 x 2 = 256
2.
3.
Ejemplos:
Apliquemos algunas propiedades para solucionar los siguientes ejercicios
NOTA: En la potenciación se debe de considerar los siguiente puntos:
1) Si la base es positiva, el resultado también sera positivo.
2) Si la base es negativa, habrá que tener en cuenta la paridad del exponente, es decir las leyes de signos:
Si esté es par, el resultado es positivo
Si es impar, el resultado es negativo.
a)falso b)Verdadero
Radicación y Logaritmación
Radicacion
RADICACIÓN
La radicación es la operación inversa de la potenciación. Si se conoce la potencia y el exponente correspondientes, se puede encontrar la base. El proceso para hallar la base se llama radicación.
Donde el símbolo  se denomina radical, n es el índice, el elemento b colocado debajo del radical es el radicando y el resultado se llama raíz. Según hemos definido la radicación, al encontrar la raíz de índice n de un número b cualquiera, consiste en determinar otro número a que multiplicado n veces por sí mismo dé como resultado el valor b. Si se conocen la potencia y el exponente correspondientes, se puede encontrar la base, el proceso para encontrar la base se llama radicación.
se denomina radical, n es el índice, el elemento b colocado debajo del radical es el radicando y el resultado se llama raíz. Según hemos definido la radicación, al encontrar la raíz de índice n de un número b cualquiera, consiste en determinar otro número a que multiplicado n veces por sí mismo dé como resultado el valor b. Si se conocen la potencia y el exponente correspondientes, se puede encontrar la base, el proceso para encontrar la base se llama radicación.
NOTA:
En los siguientes ejemplos es conveniente ver el "RECURSO WORD: Tabla de potencición" de la presente unidad.
Ejemplos:
a.(ya que
)
b.(ya que
)
c.(ya que
)
d.(ya que
)
Propiedades de la radicación:
1) La potencia de una raíz es igual a la raíz de la potencia.
Ejemplos:
a.(ya que
)
b.(ya que
)
c.(ya que
)
NOTA:
Cuando no se consigna el índice significa que éste es 2 y la raíz correspondiente se denomina cuadrada.
2) La raíz del producto de varios factores es igual al producto de las raíces de cada factor:
Ejemplos:
a.
b.(ya que
)
c.(ya que
)
3) La raíz enésima de un cociente es igual al cociente de las raíces enésimas de los respectivos valores:
Ejemplo:
a.
b.(ya que
y
)
c.(ya que
y
)
LOGARITMACIÓN
La logaritmación es otra operación inversa a la potenciación en la cual, a diferencia de la radicación, se busca el exponente al cual debo elevar un número (denominado base del logaritmo) para llegar a otro número incluido también en la operación.
NOTA:
Para los siguientes ejemplos es conveniente usar "RECURSO WORD: Tabla de potenciación"
Ejemplos:
Resolvamos los siguientes logaritmos.
a.
(El subíndice 2 representa la base del sistema)
Necesitamos saber a que potencia debemos de elevar 2 para tener 128. Mirando la tabla encontramos que el número que cumple la condición es 7. Luego tenemos:
(ya que
)
b.
Miremos la tabla para saber a que potencia se debe elevar el 8 para tener 512. El número que cumple la condición es 3. Luego tenemos:
(ya que
)
c.
Miremos la tabla para saber a que potencia debemos elevar el 10 para tener 10000. El número que cumple la condición es 4. Luego tenemos:
(ya que
)
a)
Falso b) Verdadero
EJERCICIOS DE PRACTICA 1
Esta actividad no es calificable y no tiene nota, sólo te pemite entrenarte mejor para presentar el quiz correspondiente a ésta unidad y determinar qué tanto aprendiste los conceptos y procedimientos vistos en la unidad 1.
1. Para el número 9 365 412 806 escribo qué dígito está en la posición de las:
a. Centenas.b. Decenas de mil.c. Unidades de millón.d. Unidades de mil de millón.
2. Se tiene el número 83. ¿Cuántas veces aumenta el valor representado por el 8 cuando entre los dos dígitos se escribe:
a. Un cero.b. Dos ceros.c. Cuatro ceros.
3. Usar las propiedades de la adición y sustracción para calcular los resultados.
a. 3648 + 2332 + 4320 + 1725b. 11235 + 9406 + 0 + 3465 - 20394c. -13945 + 4513 - 6152 + 22000
4. Escribir el número que hace verdadera la igualdad
a. ___ + 17 = 43b. 508 = 122 + ___c. 325 - ___ = 215
5. Utilizar las propiedades de potenciación
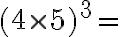
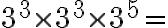
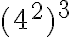
6. Completar.
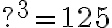
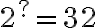
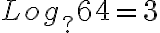
![\sqrt[6]{531441}=? \sqrt[6]{531441}=?](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/c9c13201a595fb62ae0aab2f2c2ea799.gif)
7. Señalar si es Falso o Verdadero. Justificar su respuesta.
![\sqrt[4]{1296}=6 \sqrt[4]{1296}=6](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/4665fc6ae727705f16664a0d6e4b13f6.gif)
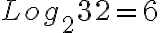
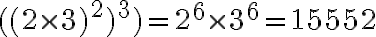
![Log_8 512=3\, es\, igual\, a\,\sqrt[3]{512}=8 Log_8 512=3\, es\, igual\, a\,\sqrt[3]{512}=8](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/64f3aaf305d4395a26874de15e2c96ca.gif)
Criterios de divisibilidad
CRIBA DE ERATÓSTENES
La Criba de Erastótenes es un método para elaborar una lista con todos los números primos menores de 100.
a. Subrayar:
- Con azul, cada segundo números después del
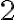 , es decir los números pares mayores que
, es decir los números pares mayores que 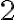 : 4, 6...
: 4, 6... - Con rojo, cada tercer número después del
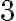 , es decir, los números mayores que
, es decir, los números mayores que 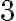 divisibles por 3: 6, 9...
divisibles por 3: 6, 9... - Con verde, cada quinto número después del
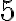 : 10, 15...
: 10, 15... - Continuar el proceso descrito, es decir, subrayar el número mayor que el seleccionado anteriormente que no ha sido subrayado, y subrayar los múltiplos correspondientes.
CRITERIOS DE DIVISIBILIDAD
Son reglas nos permiten averiguar con rapidez si un número es divisible por otro; es decir, si el mas grande es múltiplo del más pequeño.
Divisibilidad por 2:
Un número es divisible por 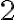 si es un número par.
si es un número par.
Divisibilidad por 3:
Un número natural es divisible por 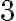 si la suma de sus cifras es un múltiplo de
si la suma de sus cifras es un múltiplo de 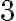 .
.
Los números subrayados con rojo en la Criba son multiplos de 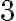 , es decir, podemos expresarlo como el producto de
, es decir, podemos expresarlo como el producto de 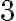 por otro número natural.
por otro número natural.
6 = 3 X 2 9 = 3 X 3
12 = 3 X 4 15 = 3 X 5
Si adicionamos los dígitos de cualquiera de los múltiplos de 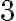 en la Criba, la suma tambiés es multiplo de
en la Criba, la suma tambiés es multiplo de 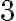 , y por tanto, el número es divisible por
, y por tanto, el número es divisible por 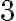 .
.
Utilizando el criterio anterior, veamos que  ,
, 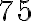 y
y  son divisibles por
son divisibles por 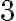 .
.
| 54 | 5 + 4 = 9 | 54 / 3 = 18 |
| 75 | 7 + 5 = 12 | 75 / 3 = 25 |
| 87 | 8 + 7 = 15 | 87 / 3 = 29 |
| Número | Suma de dígitos es divisible por 3. | Múltiplo de 3 |
Criterio para naturales de más de dos cifras.
243 : 2 + 4 +3 = 9, 243 = 3 X 81 o 243 ÷ 3 = 81
Divisibilidad por 4:
Un número es divisible por 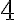 si sus dos últimas cifras son ceros o si sus dos últimas cifras forman un múltiplo de
si sus dos últimas cifras son ceros o si sus dos últimas cifras forman un múltiplo de 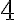 .
.
Divisibilidad por 5:
Un número es divisible por 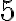 si su dígito en las unidades es
si su dígito en las unidades es  o
o 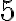 .
.
Al examinar la Criba de Eratóstenes, vemos que los números subrayados con verde 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95 y 100, son divisibles por 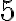 .
.
Divisibilidad por 6:
Un número es divisible por  , cuando es divisible por
, cuando es divisible por 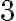 y por
y por 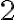 al mismo tiempo; es decir, tiene que ser par y la suma de sus cifras, múltiplo de
al mismo tiempo; es decir, tiene que ser par y la suma de sus cifras, múltiplo de 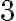 .
.
Divisibilidad por 7: Un número natural de tres cifras es divisible por  si al adicionar el doble del dígito de las decenas y la cifra de las unidades, la suma es divisible por
si al adicionar el doble del dígito de las decenas y la cifra de las unidades, la suma es divisible por  .
.
| 2 X 1 | + | 3 X 3 | + | 3 | = | 2 + 9 + 3 = 14 |
| Doble del dígito de las centenas | Triple del dígito de las decenas | Dígito de las unidades | Divisible por 7 |
En efecto,  es divisible por
es divisible por  porque 133 = 7 X 19
porque 133 = 7 X 19
Divisibilidad por 8:
Un número natural de tres cifras es divisible por  si sus tres últimas cifras son ceros o si sus tres últimas cifras forman un múltiplo de
si sus tres últimas cifras son ceros o si sus tres últimas cifras forman un múltiplo de  .
.
Divisibilidad por 9:
Un número natural de tres cifras es divisible por 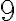 cuando la suma de sus cifras es múltiplo de
cuando la suma de sus cifras es múltiplo de 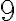 .
.
Divisibilidad por 10:
Un número natural de tres cifras es divisible por  si termina en cero.
si termina en cero.
Divisibilidad por 11:
Un números de tres cifras es divisible por  si al sustentar a la suma de los dos dígitos de las centenas y las unidades el dígito de las decenas, el resultado es múltiplo de
si al sustentar a la suma de los dos dígitos de las centenas y las unidades el dígito de las decenas, el resultado es múltiplo de  .
.

PREGUNTA:¿Cuál es el criterio de divisibilidad por 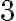 ?
?
a) Un números de tres cifras es divisible por 3 si al sustentar a la
suma de los dos dígitos de las centenas y las unidades el dígito de las
decenas, el resultado es múltiplo de 3.
b) Un número natural de tres cifras es divisible por 3 si al adicionar
el doble del dígito de las decenas y la cifra de las unidades, la suma es
divisible por 3.
c) Un número natural es divisible por 3 si la suma de los dígitos es
múltiplo de 3.
Descomposición en factores primos
DESCOMPOSICIÓN EN FACTORES PRIMOS
Como hemos visto, existen números que son primos y compuestos. Por ejemplo, 15 es un número compuesto dado que es divisible por 3 y 5:
15÷3=5
Dicho de otro modo,  ; así pues, un número compuesto puede escribirse como producto de números primos.
; así pues, un número compuesto puede escribirse como producto de números primos.
Todo número compuesto puede expresarse como producto de factores primos.
El proceso para hallar los factores primos de un número se denomina descomposición en factores primos. Existen varios caminos para realizar la descomposición en factores primos de un número. Veamos:
1) Consideremos el número 468. Para su descomposición en factores primos seguiremos el siguiente método:
468 | 2 |
En primer lugar, 468 acaba en cifra par, luego es divisible por 2. Escribimos 2 a la derecha y el resultado de la división debajo de 468.
Como 234 es también divisible por 2 colocamos otro 2 a la derecha, y debajo de 234, el correspondiente cociente.
La cifra 117 es divisible por 3; escribimos entonces 3 a su derecha y debajo de 117 el cociente resultante. Puesto que también 39 es divisible por 3, repetimos la operación obteniendo como cociente 13, que es un número primo. Por ultimo, dividimos 13 por él mismo y obtenemos la unidad. Así pues, la descomposición en factores primos del número 468 es:
que suele expresarse, despreciando el producto de 1, mediante la notación:
2) Él número 48
48 | 2 |
Otra forma de escribir un número como producto de sus factores primos es mediante la potenciación.
PREGUNTA:¿Cómo se llama el proceso para hallar los factores de un número primo?
a) Descomposición en factores primos
b) Producto de factores primos
EJERCICIOS DE PRACTICA 2
Esta actividad no es calificable y no tiene nota, sólo te pemite entrenarte mejor para presentar el quiz correspondiente a ésta unidad y determinar qué tanto aprendiste los conceptos y procedimientos vistos en la unidad 2.
1. Encierre, en la siguiente lista, los números compuestos.
42 | 83 | 19 | 66 |
72 | 39 | 108 | 79 |
196 | 134 | 59 | 236 |
2. Hallar todos los divisores de los siguientes números.
a. 25 b. 48 c. 108
3. subrayar los números divisible por 7.
56 32 49 85 87 90 91
4. Responder las siguientes preguntas:
a. ¿8 es un divisor de 0? ¿cuántos divisores tiene 0?
5. Señalo cual de de los siguientes números es divisible por 3.
a) 891 b) 73 c) 3594
6. Realizo la descomposición en factores primos de cada número.
a) 68 b) 675 c) 5435
7. Encuentro todos los divisores de cada uno de los números.
a) 56 b) 27 c) 72
8. Hallo el Maximo Divisor Común de los números dados.
a) 27 y 54 b) 100 y 230 c) 2500, 3450, 6435.
9. Encuentro el mínimo múltiplo común de cada par de números.
a) 8 y 10 b) 7 y 9 c) 58 y 595
10. Uno con una linea, cada enunciado de la izquierda con el número correspondiente en la derecha.
a. m.m.c. (9, 39) ..............................351
b. m.m.c. (27, 13) .............................936
c. Un múltiplo común de 6 y 13 ..............117
d. Un múltiplo de 36 pero no 324 ............234
Información y resolución de problemas.
PROBLEMA
Juliana, Héctor y Miguel visitan, por primera vez, la ciudad de Granada en España. Ellos quieren conocer
| Acción | Razón |
| Comprar un mapa en la ciudad | Ubicar dónde se encuentran y el sitio que quieren visitar. |
| Determinar la distancia que separa los dos sitios. | Quieren saber si pueden caminar o deben usar transporte público |
| Averiguar el horario en que el palacio esta abierto al público. | · Puede ser muy tarde para visitar el palacio. · Es posible que esté cerrado el día que quieren ir a conocerlo. |
| Averiguar el precio del boleto de entrada. | Necesitan saber cuánto dinero deben tener disponible. |
En la oficina de turismo ven un libro interesante, con fotos de cada rincón de
Organizando los gastos diarios de cada uno en una tabla, podrán decidir qué hacer.
| Gastos Diarios | |
| Desayuno | 205 pesetas |
| Transporte hotel-Alhambra | 83 Ptas. |
| Entrada a la Alambra | 750 Ptas. |
| Almuerzo | 950 Ptas. |
| Hotel | 4570 Ptas. |
| Comida | 800 Ptas. |
| Transporte Alhambra-hotel. | 83 ptas. |
a. Si hace cuatro días están en Granada, ¿Cuánto dinero han gastado en desayuno?
b. En 7 días, ¿Cuánto dinero habrán gastado en desayuno y almuerzo?
c. Si en el desayuno piden una porción de pan y queso adicional, ¿cuánto quedará costando el desayuno?
Observemos que para responder las preguntas a y b, son suficientes los datos de la tabla, y con la ayuda de algunas operaciones matemáticas, encontramos fácilmente la solución; de otra parte, para responder la pregunta c, los datos de la tabla no son suficientes.
Para resolver un problema es necesario saber cuál es el problema y que información hace falta. Después se debe organizar la información en una tabla o hacer un dibujo que ilustre el problema.
PREGUNTA: Si se quedan 4 días y 3 noches en Granada. ¿Cuánto habrán gastado por concepto de alimentación?
a) 6.070 b) 7.020 c) 5.865 d) 7.820
PROPOSICIONES
Leamos atentamente cada una de las siguientes expresiones e identifiquemos cuáles son verdaderas y cuáles falsas.
- Bogotá es la capital de Colombia.
- Brasil es el país con mayor extensión territorial en Suramérica.
- (4 + 8) x 5 = 150
- El parque arqueológico de San Agustín está en el departamento del Cauca
La expresiones a, b y d. son verdaderas; la c y la e, son falsas.
Las expresiones que podemos calificar como verdaderas o como falsas, se conocen como proposiciones.
Decir si una proposición es verdadera o falsa es asignarle el valor de verdad.
Cuál es el valor de verdad de las siguientes expresiones:
a. ¿cuándo vuelves?
b. Hasta luego
c. ¿Te gusta?
d. ¡Estoy aburrido!
e. Me siento feliz
f. 24 + 8
Estos ejemplos no pueden calificarse como verdaderos o falsos; algunos como el d o el e, dependen de la persona que los afirme o del momento en que se haga.
Se acostumbra representar las proposiciones con letras minúsculas de nuestro alfabeto; las más utilizadas son p y q.
Observemos:
p: 3 es un número primo.
q: Luís herrera fue campeón de la vuelta a Colombia.
Algunas veces utilizamos, en nuestro lenguaje, expresiones en las que empleamos dos o más proposiciones; por ejemplo: el consejo académico y el consejo directivo forman parte de nuestro gobierno escolar.
¿Cuáles son las dos proposiciones que aparecen en la frase anterior?
En efecto, la primera de ella es p: El consejo académico forma parte de nuestro gobierno escolar; la segunda es q: El consejo directivo forma parte de nuestro gobierno escolar.
Las palabras que enlazan dos o más proposiciones se llaman conectivas lógicas o partículas de enlace. Las más usuales son: y que se simboliza por  , y o que se simboliza por
, y o que se simboliza por .
.
Las proposiciones que utilizan conectivas lógicas se llaman proposiciones compuestas.
Las proposiciones compuestas son de uso común en nuestro lenguaje.
Analicemos la siguiente situación:
En la garantía de algunos automóviles aparece esta frase: “se garantiza el funcionamiento del vehículo, en condiciones de uso y mantenimiento normales, de cualquier defecto de material y de mano de obra por un periodo menor a 2 años y kilometraje menor a 40.000 kilómetros”. El 10 de julio de 1998 llegan al taller autorizado cuatro clientes.
| CLIENTE | Fecha de compra del automóvil | Kilometraje | Daño |
| Sandra Lara | Mayo 22 de 1997 | 42.008 | Eje delantero |
| José del Valle | Junio 04 de 1996 | 38.295 | Bomba de gasolina |
| Camilo Díaz. | Octubre 03 de 1997 | 35.321 | Inyección electrónica |
| Julia Escobar | Enero 09 de 1995 | 53.842 | Motor de arranque |
¿A quiénes cubre la garantía?
El conectivo que se usó entre las dos frases es y, con el cual se forma una conjunción. Por tanto, para poder recibir la garantía se deben cumplir las dos condiciones exigidas. En este caso sólo a Camilo Díaz lo cubre la garantía.
¿Por qué a los demás clientes no los cubre la garantía?
La conjunción entre dos proposiciones la representamos como p  q .
q .
Si la frase de la garantía se reemplaza por: período menor a 2 años o kilometraje menor a 40.000 kilómetros, ¿a quiénes cubre la garantía?
En este caso se tiene una disyunción, ya que el conectivo que une las frases es o. Eso significa que todos los clientes excepto Julia Escobar, tienen derecho a la garantía porque cumplen con alguna de las dos condiciones.
La disyunción entre dos proposiciones la representamos como p  q.
q.
Una conjunción se satisface si se cumplen las dos condiciones exigidas. Una disyunción se cumple cuando alguna de las dos condiciones se cumple.
PREGUNTA: ¿Cuándo es una disyunción?
a) cuando alguna de las dos condiciones se
cumple
b) cuando las dos condiciones se cumple
CONJUNTOS
Las proposiciones compuestas nos ayudan a trabajar algunas operaciones entre conjuntos. Observemos:
¿Cuáles números naturales menores que 20 son múltiplos de 2 y de 5?
El diagrama de Venn de la figura nos ayuda a organizar la información que poseemos.
La circunferencia verde encierra los múltiplos de 2.
La circunferencia morada encierra los múltiplos de 5.
En la región común de los diagramas están los múltiplos de 2 y de 5 menores que 20: (0,10)
Estos elementos pertenecen a la intersección de los dos conjuntos.
De acuerdo con la figura, ¿cuántos números naturales menores que 20 son múltiplos de 2 o de 5?
En este caso los números encerrados por alguna de las dos circunferencias son los que buscamos. Los doce números están en la unión de los dos conjuntos: {0,2, 4, 5, 6, 8, 10, 12, 14, 15, 16, 18}.
Dados los conjuntos A y B, la intersección entre ellos es el conjunto formado por los elementos que pertenecen, a la vez, a los dos conjuntos. Se simboliza 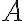

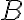
La unión entre ellos es el conjunto formado por los elementos que se encuentran en alguno de los dos conjuntos. Se simboliza 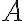

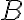 .
.
Las operaciones unión e intersección de conjuntos también nos ayudan en la resolución de problemas.
Ejemplo:
En una escuela de idiomas ofrecen cursos de inglés y de francés. En total hay 278 estudiantes. 175 del total toman cursos de inglés y 132 de francés. ¿cuántos alumnos toman ambos cursos?
Solución.
Si adicionamos los números citados, nos da una cantidad mayor 278, debido a que en el grupo de los 175 alumnos que toman clases de inglés, algunos de ellos también están tomando cursos de francés. Igual sucede con los 132 que están tomando clases de francés; en ese dato también hay alumnos que toman cursos de inglés. Eso significa que se han contado dos veces los alumnos que estudian ambos idiomas. Por tanto, debemos realizar una sustracción:
(175 + 132) - 278 = 29
Este resultado corresponde a los alumnos que toman ambos cursos. Examinemos el diagrama.
PREGUNTA: ¿Qué relación podemos concluir entre las operaciones de conjuntos y las proposiciones compuestas?
a) Que no sirve para resolver problemas de la vida cotidiano.
b) Que nos ayuda a resolver problemas de la vida cotidiano.
c) Que solo nos sirve para obtener frases completas o bien redactadas.
MÚLTIPLOS Y DIVISORES
El producto de dos o más números naturales es múltiplo de cada uno de ellos.
Se llama divisor de un número a aquel que cabe en él una cantidad de veces exacta.
Por ejemplo: Hallar los múltiplos de 36
| 36 6 1 | 6 6 |
| 36 18 6 3 1 | 2 3 2 3 |
Es visible que los divisores de 36 son 6, 2 y 3, pero, para hallar todos los divisores de 36, se obtiene multiplicando dos o tres de los números que aparecen en la descomposición en factores primos de 36.
 |  |  |
 |  |
Entonces, los divisores de 36 son: 1, 2, 3, 4, 6, 9, 12, 18 y 36. 36 es múltiplo de cada uno de sus divisores. por ejemplo 36 es múltiplo de 18 porque  .
.
Máximo Común Divisor (m.c.d)
Se llama máximo común divisor de varios números al mayor de los divisores comunes a dichos números.
Ejemplo:
| Divisores de 28 | 1 | 2 | 4 | 7 | 14 | 28 | ||
| Divisores de 42 | 1 | 2 | 3 | 6 | 7 | 14 | 21 | 42 |
Como se puede observar en la tabla el mayor divisor de 28 y 42 es 14, por tanto es el Máximo Común Divisor .
El máximo común divisor de varios números también se halla descomponiendo cada número en factores primos y multiplicando los factores comunes con menor exponente.
Este método se ilustra con el siguiente esquema:
| 72 36 18 6 | 300 150 75 25 | 252 126 63 21 | 2 2 3 |
 , por tanto el m.c.d. de 72, 300 y 252 es 12, los números 6, 25 y 21 no tienen factor primo común, razón por la cual el proceso termina aquí.
, por tanto el m.c.d. de 72, 300 y 252 es 12, los números 6, 25 y 21 no tienen factor primo común, razón por la cual el proceso termina aquí.
Mínimo Múltiplo Común (m.c.m)
El mínimo común múltiplo de dos o más números es el menor múltiplo común.
Ejemplo:
| Múltiplos de 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 |
| Múltiplos de 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 |
Como se puede observar en la tabla el menor múltiplo de 4 y 6, es 12.
El m.c.m. se puede hallar usando la descomposición en factores primos de cada número.
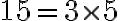 |  |
Factor común: 3
En donde, el m.c.m. de dos o más números se encuentra multiplicando los factores primos comunes y no comunes.
Otra forma para hallar el mínimo múltiplo común es con el siguiente diagrama:
| 90 | 54 | 72 | 2 |
| 45 | 27 | 36 | 2 |
| 45 | 27 | 18 | 2 |
| 45 | 27 | 9 | 3 |
| 15 | 9 | 3 | 3 |
| 5 | 3 | 1 | 3 |
| 5 | 1 | 5 | |
| 1 |
En la descomposición anterior se utilizan los números primos que dividen a todos los números de cada fila o por lo menos a alguno de ellos, hasta cuando se obtiene 1 en las distintas columnas.
PREGUNTA: ¿Cuál es el m.c.m. de 6, 15, 42?
 |  |  |
 |  |
SIGNIFICADOS DE LA FRACCIÓN
En una salsamentaría tienen dos quesos campesinos de 10 libras cada uno. Una cliente compró dos libras. ¿Qué parte de ese queso compró?. Queremos saber qué qué parte del total del queso campesino compró la cliente. Para saberlo representamos los quesos divididos en 10 pedazos iguales cada uno, como se ve en la figura, en total hay 20 libras.
Como cada pedazo de los quesos, pesa una libra, la cliente se lleva 2 de las 20 libras que había en total; eso lo representamos como  . En la salsamentaría también
. En la salsamentaría también
Para expresar una o varias partes de una unidad o de un todo se utilizan las fracciones o números fraccionarios. Estos números se representan de la forma  .
.
El número  recibe el nombre de denominador; nos indica las partes iguales en las que se divide el todo o la unidad.
recibe el nombre de denominador; nos indica las partes iguales en las que se divide el todo o la unidad.
El número  se llama numerador; nos indica la cantidad de partes iguales que se consideran.
se llama numerador; nos indica la cantidad de partes iguales que se consideran.
En una salsamentaría, venden carnes frías, en donde la siguiente tabla muestra cuantos bloques tienen de cada tipo.
Cerdo | Pollo | |
Jamón | 5 | 2 |
| Mortadela | 4 | 6 |
| Galantina | 4 | 2 |
Para expresar que hay dos bloques de jamón de pollo por 5 de jamón de cerdo, usamos la fracción  . Está fracción expresa la razón entre el número de bloques de jamón de pollo y los bloques de jamón de cerdo. La razón de bloques de galantina de pollo y los de cerdo es
. Está fracción expresa la razón entre el número de bloques de jamón de pollo y los bloques de jamón de cerdo. La razón de bloques de galantina de pollo y los de cerdo es  . Es decir, por cada bloque de galantina de pollo hay dos de galantina de cerdo.
. Es decir, por cada bloque de galantina de pollo hay dos de galantina de cerdo.
En la tabla, nos muestra 4 bloques de mortadela de cerdo por 6 de mortadela de pollo, luego, por cada bloque de mortadela de pollo hay  bloques de mortadela de cerdo.
bloques de mortadela de cerdo.
La fracción que expresa la comparación entre dos cantidades de la misma magnitud se llama razón.
PREGUNTA: En una salsamentaría tienen un bloque de queso doble crema de 10 libras, del cual una cliente compró 3 libras. ¿Qué parte del queso crema compró?
a)10/3 b) 3/10 c) 1/3
FRACCIONES EQUIVALENTES
El profesor de deportes convoca dos grupos de estudiantes de grado sexto para seleccionar aquellos que integrarán el equipo de baloncesto. El primer grupo lo forman cinco estudiantes más altos del curso; en el segundo grupo están los 10 estudiantes más ágiles.
A la hora de conformar el equipo, el profesor elige 3 estudiantes del primer grupo y 6 del segundo grupo.
Un estudiante del curso pregunta: ¿por qué seleccionó más del segundo grupo? Para ser equitativo con ambos, responde el profesor. ¿Qué parte de cada grupo tomó el profesor?. En el primer grupo, de 5 alumnos que hay, el profesor tomó 3; en el segundo, de 10 alumnos llamó a 6, es decir, se seleccionaron los  y los
y los  de cada grupo respectivamente.
de cada grupo respectivamente.
Las fracciones que representan la misma parte de un todo reciben el nombre de fracciones equivalentes.
Las equivalentes difieren únicamente en su expresión. En el caso que nos ocupa, el profesor selecciono  del primer grupo y
del primer grupo y  del segundo. Observamos que los términos de la segunda fracción se obtienen multiplicando los términos de la primera fracción por 2; los términos de la primera se obtienen dividiendo los términos de la segunda por 2.
del segundo. Observamos que los términos de la segunda fracción se obtienen multiplicando los términos de la primera fracción por 2; los términos de la primera se obtienen dividiendo los términos de la segunda por 2.
El proceso de multiplicar el numerador y el denominador de una fracción por un número natural se conoce como amplificación.
Ejemplo:
Amplifiquemos por 3 la fracción 
Multiplicamos el numerador y el denominador por 3:
El proceso de dividir el numerador y el denominador de una fracción por un mismo divisor común a ellos se conoce como simplificación.
Ejemplo:
En este caso 3 es divisor común de ambos término, por tanto, podemos dividir simultáneamente.  , observemos que
, observemos que 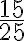 es una fracción que aún se puede simplificar más dividiendo ahora por 5, así:
es una fracción que aún se puede simplificar más dividiendo ahora por 5, así:  . La fracción
. La fracción  no se puede seguir simplificando.
no se puede seguir simplificando.
Cuando una fracción no se puede simplificar la llamaremos fracción irreducible.
Para encontrar fracciones equivalentes a una fracción dada basta con amplificar o simplificar la fracción.
PREGUNTA: La fracción equivalente de  es:
es:
a) 18/35 b)15/42 c) 12/42 d) 18/42
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES HOMOGÉNEAS
ADICIÓN
La adición de fraccionarios con igual denominador es una fracción: Cuyo numerador es la suma de los numeradores de los fraccionarios y el denominador es el mismo de ellos.
Ejemplo:
SUSTRACCIÓN
La sustracción de fraccionarios con igual denominador es una fracción: Cuyo numerador es la diferencia entre los numeradores de los fraccionarios (siempre que sea posible realizarla) y el denominador es el mismo de ellos.
ADICIÓN Y SUSTRACCIÓN DE FRACCIONES HETEROGÉNEAS
Para la adición de fraccionarios con diferente denominador se buscan fracciones equivalentes con igual denominador y se adicionan. De igual manera, para sustraer fraccionarios con diferente denominador se busca fracciones equivalentes con igual denominador y se sustraen (siempre que sea posible).
Ejemplo:
Realicemos la suma de las fracciones 
Solución:
El mínimo múltiplo común entre 4 y 5 es 20, entonces: Debes dividir el m.c.m. que en este caso es 20, por los denominadores (4 y 5) y el cociente de está división, lo debes multiplicar por el numerador de cada fracción y dejando como denominador el m.c.m.
a)2/4 b) 1/4 c) 1/8 d) 10/40
MULTIPLICACIÓN
Para multiplicar dos o más fracciones, se multiplican "en línea". Esto es, el numerador por el numerador y el denominador por el denominador.
Ejemplo:
Cuando el producto de números fraccionarios es 1, se dice que cada uno de ellos es recíproco del otro. Un fraccionario con numerador 0 no tiene recíproco.
Ejemplo:
Solución:
DIVISIÓN
Para dividir dos o más fracciones, equivale a multiplicar el primero por el inverso del segundo, es decir, dadas las fracciones  y
y 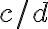 ,
,
Ejemplo:
a)20/3 b) 10/12 c) 20/6 d) 10/6
EJERCICIOS DE PRACTICA 4
Esta actividad no es calificable y no tiene nota, sólo te pemite entrenarte mejor para presentar el quiz correspondiente a ésta unidad y determinar qué tanto aprendiste los conceptos y procedimientos vistos en la unidad 4.
1. Para cada fracción de la tabla, encuentra fracciones equivalentes.
Fracciones Equivalentes | ||
Por | Por | |
|
| |
|
| |
|
| |
2. Simplifico hasta obtener una fracción irreducible.
3. Encuentro la suma de las fracciones y simplifico
4. Encuentro la diferencia entre las fracciones dadas
5. Encuentro el producto y doy la respuesta en una fracción irreducible.
6. Encuentro la fracción resultante
7. Digo si cada expresión es falsa o verdadera y explico mi respuesta.
8. Margarita confecciona disfraces para el carnaval de su pueblo. algunos van decorados con cintas de distintos colores y longitudes.
a. De cinta azul compró tiras de 3 m para cortar pedazos de
m de cada uno. ¿Cuántos pedazos de cinta azul obtiene de una tira?
b. Las tiras de cinta roja miden
m; si cada una de ellas margarita debe cortar pedazos de
m, ¿cuántos pedazos puede cortar de la tira roja?.
NÚMEROS DECIMALES
Las fracciones se pueden escribir en forma de números decimales. La fracción 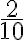 puede representarse con una expresión decimal así: 0,2. Es decir:
puede representarse con una expresión decimal así: 0,2. Es decir: 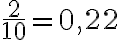 .
.
En cada expresión decimal encontramos una parte entera y una parte decimal.
En la expresión 19,834 tenemos
Dependiendo del número de cifras decimales, estas expresiones se leen de una manera especial, por ejemplo:
 se lee trescientos cincuenta y ocho milésimas.
se lee trescientos cincuenta y ocho milésimas.
Una fracción decimal es aquella que tiene como denominador una potencia de 10.
Una expresión decimal también puede escribirse en una tabla de valor posicional.
Observemos cómo se ubican en la tabla los números 14,5 y 2,30
Hemos ubicado los decimales: 14 enteros, 5 décimas; 2 enteros, 30 centésimas.
PREGUNTA: ¿la expresión  es una fracción decimal?
es una fracción decimal?
Sitio web sobre decimales
https://www.profesorenlinea.cl/matematica/Decimales.htm
EXPRESIONES DECIMALES EN LA RECTA NÚMERICA
La recta numérica es una línea recta en la que asociamos cada número con un punto de la recta
Expresiones como 0.5, representan un punto en la recta. En este caso el punto 0.5 se encuentra entre 0 y 1; observemos la figura:
Si el segmento entre 0 y 1 se divide en 10 partes iguales, cada parte corresponde a una décima.
Ejemplo:
Ubiquemos en una recta numérica el punto 1.5.
El número 1.5 lo podemos escribir como 1 + 0.5, de esta forma sabemos que 1.5 está ubicado entre 1 y 2, veamos la figura:
PREGUNTA: En la siguiente recta ubicar el valor correspondiente al punto señalado por el interrogante:

a) 1.8= 18/10 b) 1.6 = 16/10 c) 1.7 =17/10 d) 1.5=15/10
COMPARACIÓN Y ORDENACIÓN DE DECIMALES
Para comparar decimales se siguen un procedimiento bastante sencillo, veamos.
Ejemplo:
- En cada numeral se buscan, de izquierda a derecha, los primeros dígitos que sean distintos: 0.8 3 7 0.8 4 7
- Se comparan esos dígitos:
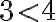
- Luego, se comparan los números dados:
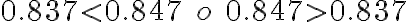
Ejemplo 2:
Como 1 y 0 son los primeros dígitos diferentes, y 1 > 0, entonces:
PREGUNTA: Comparar los números 
a) 2.326 < 2.325 o 2.325 >
2.326 b) 2.326 > 2.325 o 2.325
< 2.326
c) 2.326 > 2.325 o 2.325 > 2.326 d) 2.326 < 2.325 o 2.325
< 2.326
DECIMALES PERIÓDICOS
Recordemos que de una fracción se puede obtener un número decimal con sólo dividir el numerador entre el denominador.
Algunas veces el proceso de división parece no terminar. Veamos.
Ejemplo:
Encontremos la expresión decimal de la fracción 
Dividiendo el numerador entre el denominador obtenemos:
En  , los puntos suspensivos significan que los dígitos 4 y 5 se repiten indefinidamente en ese mismo orden.
, los puntos suspensivos significan que los dígitos 4 y 5 se repiten indefinidamente en ese mismo orden.
El número decimal que contenga en su parte decimal un dígito o grupo de dígitos que se repitan indefinidamente en un orden secuencial, se llama número decimal periódico.
El dígito o grupo de dígitos que se repite se llama período.
Para indicar cuál o cuáles dígitos forman el periodo de un número decimal, se coloca, sobre ellos, una barra horizontal, así: 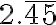
Ejemplo:
Encontremos la expresión decimal de la fracción 
En este caso si se continúa dividiendo después de obtener residuo 0, el dígito que aparecería en el cociente, en cada paso, seria cero.
Por tanto:  . Que generalmente se abrevia escribiendo: 1.1875.
. Que generalmente se abrevia escribiendo: 1.1875.
Si al realizar la división entre el numerador y el denominador de una fracción obtenemos 0 en el residuo, llamaremos al cociente número decimal finito o exacto.
Números decimales como:
0.10100100010000…
0.12345678901122…
0.20220222022220…
Reciben el nombre de números decimales no periódicos.
PREGUNTA: La expresión decimal de la fracción 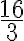 es:
es:
* Número decimal no
periódico * Número decimal
finito * Número decimal periódico
ADICIÓN Y SUSTRACCIÓN DE DECIMALES
La adición y sustracción de decimales siguen las mismas reglas de la adición y la sustracción de los números naturales. Veamos:
Ejemplo:
Adicionemos 0.68 y 0.4
- Debemos alinear el punto de los números decimales.
- Afectamos la operación colocando el punto del resultado alineado con el de los sumandos.
Ejemplo 2:
Restemos 121.46 de 265.3
- Los números dados deben tener la misma cantidad de cifras decimales. Si no es así, completamos colocando ceros.
- Alineamos le punto de los números decimales
- Efectuamos la operación.
PREGUNTA: Restar 256,012 de 324,1
MULTIPLICACIÓN DE DECIMALES
Cecilia hornea una cerámica para el día de la madre. La cerámica debe permanecer 3 horas en el horno. Si la electricidad que consume el horno cuesta $ 107.48 por hora, ¿Cuál es el costo del consumo de electricidad en las 3 horas?
Para solucionar esta situación multiplicamos $ 107,46 por 3.
- La multiplicación de un decimal por un natural se hace como si se tratara de números naturales.
- El producto tiene tantas cifras decimales como la suma de las cifras decimales de los números dados.
En el resultado hay dos cifras decimales.
Ejemplo:
Multipliquemos 4,27 y 0,7
- Multiplicamos como si fueran números naturales
- El producto lo escribimos con tantas cifras decimales como la suma del numero de cifras decimales de los factores:
PREGUNTA: multiplicar 0,008 por 0,3
MULTIPLICACIÓN POR 10, 100, 1000
Al multiplicar un número decimal por 10, se desplaza la ubicación del punto decimal un lugar hacia la derecha.
PREGUNTA: Multiplicar 2.5648 por 10000
DIVISIÓN DE NÚMEROS DECIMALES
La división de un número decimal entre un número natural se realiza como se muestra en el siguiente ejemplo.
Ejemplo:
Pasos | Procedimiento |
Dividimos la parte entera del número entre el divisor | |
Colocamos el punto decimal en el cociente y bajamos la cifra de las décimas; luego, continuamos la división. |
|
Después bajamos las centésimas y dividimos. Así sucesivamente. |
Para dividir un decimal entre otro decimal se sigue el procedimiento que se muestra a continuación.
Ejemplo:
Pasos | Procedimiento |
Multiplicamos el dividiendo por 10, 100, 1000 o la potencia de 10 que sea necesaria para convertirlo en un número natural. 3.24 X 100 = 324 |
|
Para continuar la división agregamos un cero al residuo y colocamos un punto decimal en el cociente. | |
Multiplicamos el divisor por la misma potencia de 10. 1.2 X 100 = 120 | |
Efectuamos la operación |
De la misma manera se trabaja si deseamos dividir un numero natural entre un número decimal.
En la división al igual que en la multiplicación, podemos dividir abreviadamente por 10, 100, 1000 o cualquier otra potencia de 10.
Ejemplo:
Dividamos 187.92 entre 10.
En este caso, corremos el punto un lugar hacia la izquierda y obtenemos: 18.792.
Dividamos 69.51 entre 1000.
PREGUNTA: Dividir 2.54 entre 100
EJERCICIOS DE PRACTICA 5
Esta actividad no es calificable y no tiene nota, sólo te pemite entrenarte mejor para presentar el quiz correspondiente a ésta unidad y determinar qué tanto aprendiste los conceptos y procedimientos vistos en la unidad 5.
a. 1,11 ____ 1,12
b. 0,84 ____ 0,48
c. 0,370 ____ 0,30
d. 5,89 ____ 5,891
e. 1,101 ____ 1,10101
f. 0,002 ____ 0,00200
2. Escribir si es Falso o Verdadera cada igualdad. Explicar su respuesta.
a. 5,3000 = 5,300 = 5,30 = 5,3
b. 25 = 25,0 = 25,00 = 25,000
c. 0,0001 = 0,001 = 0,01 = 0,1
d. 0,0002 = 0,002 = 0,0201 = 0,2
3. Realizo la operación indicada
a. 7,4 + 2,01 + 0,05
b. 1,00 + 3,001 + 1,999
c. 2,54 – 1,05 – 0,4
d. 3,4 + 5,42 – 6,4 – 0,002
4. La diferencia de dos números decimales es 0,87. Si el mayor de los números es 1,43. ¿Cuál es el valor del otro número?
5. Una cancha de básquetbol mide 26 m de largo por 14 m de ancho. Si la cancha para menores mide 7,50 metros menos de largo y 1,25 metros. ¿cuáles son sus medidas?
6. La economía de gasolina en un automóvil se refiere a cuántos kilómetros puede recorrer con un galón. Para determinar la economía de gasolina en cualquier vehiculo se usa la división.
Gasto de gasolina = Número de kilómetros 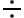 Número de galones gastados
Número de galones gastados
Utilizo la tabla para determinar cuál de las marcas es más económica.
Distancia recorrida en Km. | Cantidad de galones | |
Marca 1 | 24,8 | 12 |
Marca 2 | 24,8 | 24 |
Marca 3 | 24,8 | 16 |
Marca 3 | 24,8 | 14,2 |
7. Una fábrica de uniformes necesita 1,6 metros de tela para confeccionar un pantalón para niño y 0,8 metros para hacer las faldas de las niñas. ¿Cuánta tela necesita la fabrica, si un colegio de bachillerato tiene 30 profesores y 420 alumnos, de los cuales el 200 son niños?
vídeo escribiendo un decimal representar cantidades
MEDICIÓN
- La Cuenca Amazónica se extiende unos
 km²
km² - Una familia de 4 personas usa alrededor de
 litros de agua a la semana
litros de agua a la semana - Una ballena puede llegar a pesar
 toneladas y medir más de
toneladas y medir más de 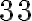 m.
m. - Un glóbulo rojo de sangre mide
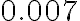 mm de diámetro.
mm de diámetro.
¿Por qué estos datos son importantes? Todos ellos nos dan información sobre una medida, pero si solo lo podemos comparar con otras medidas que conozcamos, podremos apreciarlos. Por ejemplo, si sabemos que un carro pequeño pesa alrededor de una tonelada, podremos percibir lo grande que es una ballena; si supiéramos que Colombia tiene una superficie de 1.141.568 km², quedaríamos impresionados por el tamaño de la cuenca Amazónica, cuya superficie es aproximadamente siete veces Colombia.
Aquellas propiedades de los objetos que se pueden medir, se llaman magnitudes. Algunas de ellas son: longitud, área, peso, volumen y capacidad.
La información que obtenemos acerca de una medida nos permitirá tener una noción sobre el tamaño, la capacidad o la duración de un objeto o fenómeno. En la vida diaria utilizamos la estimación para darnos una idea de una medida.
El proceso de asignar un número a una magnitud puede hacerse de dos maneras:
Informal: Cuando la medida no requiere precisión, solo se necesita tener una idea.
Formal Cuando la medida requiere de exactitud, pues de ello dependen decisiones importantes.
Usamos unidades de medida apropiadas, instrumentos adecuados y personas con habilidad para manejarlos.
La unidad de medida
Para comparar magnitudes se usa un patrón común de medida.
La necesidad de comunicar los resultados de una medición lleva a la unificación de las unidades de medida.
En la siguiente tabla, algunas unidades de medida comunes.
En el siguiente vídeo encuentra un ejemplo y características que le ayudarán a entender mejor el tema
PREGUNTA: Al transportarme de mi casa al colegio,¿Qué magnitudes puedo utilizar?.
* Tiempo y área. * Tiempo y peso.
* Longitud y tiempo. * Longitud y
Volumen.
MEDIDAS DE LONGITUD
La medida de un objeto se expresa generalmente con aproximaciones. La búsqueda de mayor precisión nos obliga a usar unidades cada vez más pequeñas.
Tal como fue diseñado nuestro sistema decimal, cada unidad es la décima parte de la unidad inmediatamente anterior.
Una medida de longitud se puede expresar en distintas unidades aplicando el siguiente proceso:
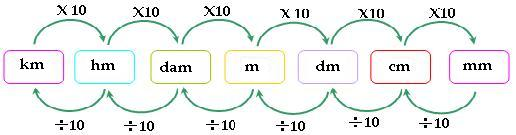
Medida de áreas
Hallar el área de una superficie consiste en determinar el número de unidades cuadradas que caben en dicha superficie.
Nuestro sistema decimal de medidas hace 100 divisiones de cada unidad de área. Por ejemplo, observamos que  equivale a
equivale a 
Una medida de área puede expresarse en distintas unidades aplicando el siguiente proceso:
Ejemplo:
Ahora vamos a ver el cálculo del área de lagunas figuras conocidas
Área de un rectángulo
El área de un rectángulo se obtiene encontrando el producto de sus dimensiones (base X altura)
Área de un paralelogramo
El área de un paralelogramo es el producto de la longitud de la base por la longitud de la altura. Por tanto el área del paralelogramo es el mismo que el del rectángulo.
Área de un triángulo
El área de un triangulo es el producto su base por la altura, dividido en dos
Área del círculo
El área de un círculo es igual al valor de su radio elevado al cuadrado multiplicado por 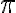 .
.
PREGUNTA: Si tengo una finca en forma rectangular, cuyas medidas son: 100 m de largo por 10 m de ancho. ¿Cuál es el área de la finca?
* 100000 m2 * 10000 m2 * 100 m2 * 1000 m2
MEDIDA DE ÁNGULOS
La medida de los ángulos permite clasificarlos en:
· Dos ángulos son complementarios si la suma de sus medidas es 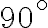
· Dos ángulos son suplementarios si la suma de sus medidas es 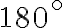
Ejemplo:
¿Cuál es el complemento y el suplemento de un ángulo de 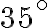 ?
?
Para hallar el complemento de un ángulo de 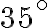 utilizamos la sustracción
utilizamos la sustracción 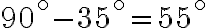
De otro lado, el suplemento de un ángulo de 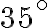 es
es 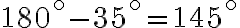
PREGUNTA: ¿Cuál es el ángulo complemento de  ?
?
a) 75º b) 165º c) 155º d) 85º
NOTACIÓN CIENTÍFICA
“La mayor parte de las estrellas son de tamaño semejante al Sol, cuyo diámetro es 1.400.000 km, aunque algunas son cien veces más grandes, es decir, de  de km de diámetro. La mas grande que se ha detectado hasta ahora es la estrella de doble Pedilón Aurige, cuyo diámetro es
de km de diámetro. La mas grande que se ha detectado hasta ahora es la estrella de doble Pedilón Aurige, cuyo diámetro es  de km. Si esta estrella fuera como un balón de fútbol, el Sol seria como un grano de sal”.
de km. Si esta estrella fuera como un balón de fútbol, el Sol seria como un grano de sal”.
Para facilitar la escritura de números tan grandes los científicos usan un sistema de numeración llamado notación científica.
Ejemplo:
Expresemos en notación científica el numero 1.400.000
Solución:
El numero se escribe como el producto de dos factores. El segundo factor es una potencia de 10.
El primer factor se escribe como el producto de un numero entre 1 y 10 por una potencia de 10.
Se multiplican las potencias de 10.
La notación científica se usa para expresar cantidades en potencias de 10. El exponente en la potencia de 10, representa el número de lugares que se corre la coma decimal en el primer factor.
Ejemplo:
Expresemos 3.000.000.000 en notación científica
Escribamos 45.000 utilizando notación científica
En notación científica, todas las cantidades se escriben como el producto de un número entero entre 1 y 10 por un potencia de 10.
PREGUNTA: Expresar en notación científica el numero 1.425.000
* 1.425\timesx106 * 1.425\timesx103 * 1.425\timesx107 * 1.425\timesx105
Estamos rodeados por objetos cuya forma corresponde a un sólido geométrico. Algunos de esos objetos, como los cristales de sal o los panales de las abejas, existen en la naturaleza y otros son fabricados por el hombre.
Vamos a ver algunos ejemplos de figuras sólidas:
Excepto el cilindro, los sólidos construidos tienen caras planas, aristas y vértices.
Estos sólidos reciben el nombre de poliedros. Un poliedro se puede distinguir los siguientes elementos:
- Vértices: que son los puntos del poliedro en los que se reúnen tres o más aristas
- Aristas: que son los segmentos en los que se encuentran dos caras
- Caras: que son las porciones de plano que limitan el cuerpo, tienen forma de polígono.
Las caras, aristas o vértices de los sólidos nos sugieren los elementos con los que trabajamos en geometría.
La huella que deja un vértice de un poliedro sobre una hoja nos da la idea de punto.
Para nombrar los puntos utilizaremos letras mayúsculas del alfabeto.
La huella que deja un arista del poliedro nos da la idea de un segmento.
Al prolongar indefinidamente un segmento en ambos sentidos obtendremos una línea recta.
Un segmento es una parte de la recta que tiene dos puntos extremos.
Semirrecta o rayo es una parte de la recta que tiene un punto origen y se prolonga indefinidamente en un sentido.
Estos elementos geométricos se denotan de la siguiente manera:
PLANO
Definición de plano
Usualmente los planos los nombramos con letras del alfabeto griego. Las más utilizadas son 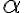 (alfa),
(alfa),  (beta),
(beta), 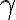 (gamma).
(gamma).
Un ángulo es una figura formada por dos semirrectas que tienen el mismo origen.
En la siguiente figura observamos la representación gráfica de un ángulo.
Los lados de un ángulo se pueden prolongar indefinidamente.
Llamaremos los ángulos citando los puntos que nombran las semirrectas. El ángulo de la figura anterior lo llamaremos  BDE o
BDE o  EDB. Lo leemos ángulo BDE o ángulo EDB.
EDB. Lo leemos ángulo BDE o ángulo EDB.
El vértice debe quedar entre los otros dos puntos.
Dos figuras son congruentes cuando tienen la misma forma y el mismo tamaño.
Dos rectas que están en el mismo plano y no se intersectan se llaman paralelas. Escribimos para decir “la recta
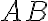 es paralela a la recta
es paralela a la recta  ”.
”.
Dos rectas que forman ángulos rectos se llaman perpendiculares. Escribimos para decir “la recta
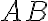 es perpendicular a la recta
es perpendicular a la recta  ”.
”.
PREGUNTA: Dos rectas son paralelas cuando:
POLÍGONOS
Un polígono es una figura geométrica formada por la unión de segmentos que se unen sólo en sus extremos, de tal manera que como máximo dos segmentos se encuentran en un punto y cada segmento toca exactamente a otros dos.
La siguiente figura nos muestra las partes de un polígono:
Un polígono equilátero es un polígono cuyos lados son congruentes entre sí.
Un polígono regular es aquel cuyos lados y ángulos son congruentes entre sí.
Una diagonal de un polígono es un segmento cuyos extremos son vértices, del polígono, no consecutivos.
CLASES DE TRIÁNGULOS
Los triángulos son los polígonos de menor número de lados. Podemos calcificarlos de acuerdo con la medida de sus ángulos y medida de sus lados.
CLASES DE CUADRILÁTEROS
Los polígonos de cuatro lados se llaman cuadriláteros. Los cuadriláteros planos convexos pueden clasificarse por la posición relativa de los lados:
- Los cuadriláteros que tiene paralelos sus dos lados opuestos se denominan paralelogramos.
- Los cuadriláteros que tienen un solo par de lados paralelos opuestos se llaman trapecios
- Los cuadriláteros que no tienen ningún par de lados paralelos opuestos se llaman trapezoides.
Recordemos algunos muy familiares:
En un cuadrilátero podemos identificar los elementos que muestra la siguiente figura:
En general los polígonos los podemos clasificar de acuerdo con el número de lados.
PREGUNTA: ¿Un polígono equilátero es?
MOVIMIENTO EN EL PLANO
Cuando un punto se desplaza sobre un plano describe una trayectoria, que puede ser recta o curva.
Todos los movimientos describen una trayectoria, aunque a veces no podamos percibirla. Por ejemplo, cuando vamos para el colegio seguimos un camino que describe una trayectoria, ya sea recta o curva.
Cuando vemos pasar un avión por el aire, también podemos describir una trayectoria; los movimientos que realiza la Tierra, aunque no los apreciemos, si podemos describirlos.
La traslación es el movimiento de una figura a lo largo de una línea recta, una distancia dada, con un sentido y una dirección.
En la siguiente figura, la traslación se ha realizado a lo largo de la recta  , 12 cm, en el sentido de A y B.
, 12 cm, en el sentido de A y B.
Para hacer una traslación debemos tener en cuenta los elementos que se destacan en la figura.
El resultado de trasladar una figura es otra figura llamada imagen. Cada uno de los puntos en la figura imagen se nombra colocando una coma en la parte superior derecha de cada letra, como se aprecia en el siguiente ejemplo:
Ejemplo:
Traslademos el polígono ABCDE en la dirección, sentido y distancia indicados en la figura:
La figura A' B' C' D' E' F'es la imagen de la figura ABCDEF después de realizar la traslación.
Las letras A' B' C' D' E' F' reciben el nombre de primas. Se leen: A prima, B prima…… y así sucesivamente.
ROTACIONES
El movimiento que realiza una figura alrededor de un punto fijo se denomina rotación. El punto fijo se llama centro de rotación.
Si el movimiento de la figura gira en sentido de las manecillas del reloj, diremos que se mueve en sentido negativo. En caso contrario, el movimiento será en sentido positivo.
En toda rotación se pueden identificar:

La amplitud de una rotación se expresa en grados.
Para indicar que una figura es el resultado de una rotación, utilizamos letras primas.
PREGUNTA:La traslación es el movimiento de un figura a lo largo de:
EJERCICIOS DE PRACTICA 6
Esta actividad no es calificable y no tiene nota, sólo te pemite entrenarte mejor para presentar el quiz correspondiente a ésta unidad y determinar qué tanto aprendiste los conceptos y procedimientos vistos en la unidad 6.
1. Expresar:
a) En centímetro:
· 20 mm
· 2.33 Km.
· 542 dam
b) En m.
· 412.23 hm
· 934.33 km
· 2344 cm
2. Determinar el área de la siguiente figura
3. Completo la tabla
Medida del ángulo | 50º | 140º | ||
Medida de su complemento | 72º | |||
Medida de su suplemento | 150º |
4. Efectuó las operaciones y expreso el producto en notación científica
5. Leonardo Euler, matemático suizo, hallo una formula que relaciona aristas (A), caras (C) y vértices (V) de un poliedro:
Verifico la formúla de Euler para los siguientes poliedros.
6. Escribo Falso (F) o Verdadero (V) según el caso:
a) Todos los cuadrados son paralelogramos
b) Un trapecio puede tener dos ángulos rectos
c) Todos los rectángulos son paralelogramos
d) Todo triangulo equilátero es isósceles
e) Todo triangulo rectángulo es escaleno
7. Completo los espacios colocando los símbolos 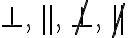 de acuerdo con la información dad en la siguiente figura:
de acuerdo con la información dad en la siguiente figura:
8. La figura 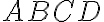 se ha trasladado dos veces según la flecha OP. Completa:
se ha trasladado dos veces según la flecha OP. Completa:
a) La imagen del punto
en la primera traslación es _____
b) La imagen del punto
es _____
RAZÓN
La Razón es una comparación entre dos cantidades o dos números. Las razones se escriben  y se leen: a es a b.
y se leen: a es a b.
Las razones también se pueden escribir en forma de fracción: 
Toda razón genera nuevas razones, por ejemplo, la razón 1 es a 4 da origen a las razones 2 es a 8 y 4 es a 16.
Ejemplo:
 Si se sabe que por cada peldaño de la escalera de la figura a hay dos clavos, ¿cuántos clavos hay en
Si se sabe que por cada peldaño de la escalera de la figura a hay dos clavos, ¿cuántos clavos hay en 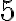 peldaños?; ¿cuántos hay en
peldaños?; ¿cuántos hay en  peldaños?
peldaños?
Solución:
En cada peldaño la escalera tiene dos clavos, lo que da origen a la razón.
Con esta razón pueden formarse nuevas razones:
De esta forma concluimos que en 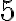 peldaños hay
peldaños hay  clavos y que en
clavos y que en  peldaños hay
peldaños hay  clavos.
clavos.
PREGUNTA: La razón 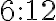 da origen a la razón:
da origen a la razón:
PROPORCIONES
Una proporción es una expresión que muestra la igualdad entre dos razones.
 se lee: a es a b como c es a d.
se lee: a es a b como c es a d.
a y d se llaman extremos
b y c se llaman medios
Otra forma de escribir la proporción  es
es 
Ejemplo:
Doña Mariela tiene para esta semana en su venta de flores, una promoción: 5 rosas por $2.000. Gloria quiere comprar 15 rosas.
¿cómo calcula doña Mariela el precio de las 15 rosas?
Si ordenamos los datos obtenemos:
Rosas | Precio $ |
5 | 2000 |
X 3 | X 3 |
15 | 6000 |
15 rosas cuestan $ 6.000
En esta situación tenemos:
O porque  es una fracción equivalente a
es una fracción equivalente a 
Otra manera de comprobar que dos razones son iguales es efectuando el producto de extremos y el producto de medios: si obtenemos el mismo resultado, decimos que las razones son equivalentes y, por tanto, generan una proporción.
Si los resultados que se obtienen son diferentes, las razones no generan una proporción.
PREGUNTA: Encuentro el valor desconocido en la siguiente expresión, de tal forma que se obtengan fracciones equivalentes: 
a) 20 b) 15 c) 30 d) 25
PORCENTAJE
Cuando en una razón el número con el que se compara es 100, la razón expresa un porcentaje.
Porcentaje significa por ciento y se escribe %
Ejemplo:
Expresemos en porcentajes, las razones 
De otra parte, un porcentaje puede escribirse en forma de razón.
Ejemplo:
Recordemos que una fracción se puede escribir en forma decimal.
Como un porcentaje representa una fracción donde el denominador es 100, entonces podemos concluir que:
Hasta el momento hemos relacionado los porcentajes con números decimales y con fracciones cuyo denominador es 100. El siguiente ejemplo nos muestra que podemos relacionar porcentajes con otras fracciones.
Ejemplo:
La gráfica circular de la siguiente figura muestra los resultados de una encuesta de opinión realizada a los estudiantes de un colegio, para determinar cambios en el horario de entrada.
¿Qué fracción del círculo representa a los estudiantes que no están de acuerdo con el cambio de horario?
 . Simplificando la fracción
. Simplificando la fracción 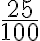 obtenemos
obtenemos  .
.
Por tanto, la fracción que representa a los estudiantes que no están de acuerdo con el cambio de horario es 
Algunas veces una fracción puede escribirse como fracción decimal para luego expresarla como porcentaje.
Por ejemplo, para escribir  en forma de porcentaje seguimos estos pasos:
en forma de porcentaje seguimos estos pasos:
Convertimos  en una fracción decimal. en una fracción decimal. |  |
| Escribimos el porcentaje |  |
PREGUNTA: Expresa 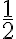 como un porcentaje
como un porcentaje
a)50% b)20%
c)75% d)25%
PORCENTAJE DE UN NÚMERO
Para hallar el porcentaje de un número debemos seguir este procedimiento:
Porcentaje de un número | |
Expresamos el porcentaje como fracción o como decimal | |
Hallamos el producto entre la expresión decimal o la fracción y el número al cual se le va a encontrar el porcentaje. | |
Ejemplo:
Encontrar el 30% de 120.
Solución:
Otra forma es:
Ejemplo 2:
¿Cuál es el 25% del 82% de 500?
Solución:
- Primero debemos calcular el 82% de 500
Así concluimos que el 25% del 82% de 500 es 102,5.
PREGUNTA: El 13% de 3000 es:
Números relativos
Los números relativos están compuestos de tres grupos de números:
- Números relativos positivos: Son los números mayores de 0.
Por ejemplo: +1, +2, +3, ... Los números positivos se pueden escribir también así (+3), (+4)...
Cuando al frente de un número no hay ningun signo, siempre se tomara como positivo. 1, 2, 3...
- Números relativos negativos: Son los números menores de 0.
Por ejemplo:-3, -2 , -1 ...; (-1), (-2), (-3)...
NOTA: Mientras más grande parezca un número negativo, realmente es más pequeño.
- El cero: El cero es un número relativo pero no es ni positivo ni negativo.
Por lo tanto, aquí mostraremos la lista que representa todos los números relativos.
... ,-5, -4, -3, -2, -1, 0, +1, +2, +3, +4, +5, ...
Representación gráfica de los números relativos
COMPARACIÓN DE NÚMEROS RELATIVOS:
En matemáticas siempre se ha comparado dos números para saber cual es más grande y cuál es el menor.
Para indicar estas relaciones se utiliza los siguientes signos:
> Mayor que
< Menor que
Ejemplo: ¿Cuál número es el mayor entre -8 y -2?.
Dos negativo es mayor que ocho negativo, q se puede escribir así: -8<-2
SUMA DE NÚMEROS RELATIVOS
Cuando sumas números relativos, se puede dar las siguientes circunstancias:
- Cuando los dos números son positivos: Siempre da positivo.
Ejemplo: (+2) + (+3) = + 5 - Cuando los dos números son negativos: Se suman y se deja el signo negativo a la respuesta.
Ejemplo: (-2) + (-2) = - 4 - Cuando uno de los dos números es positivo y el otro es negativo: Se restan y se deja el signo del mayor.
Ejemplo 1: (-3) + (+4) = + 1.
Ejemplo 2: (+3) + (-5) = - 2. En este caso el 5 es mayor que 3, por lo que se deja el signo negativo a la respuesta.
PREGUNTA: (+3) + (-7) = + 4. Falso o verdadero
De los números relativos a los números enteros
Los números enteros son una generalización del conjunto de números naturales que incluye números enteros negativos (resultados de restar a un número natural otro mayor), además del cero. El hecho de que un número sea entero, significa que no tiene parte decimal.
Los números enteros negativos pueden aplicarse en diversos contextos, como la representación de profundidades bajo el nivel del mar, temperaturas bajo cero, o deudas, entre otros.
El preparador físico de un equipo de fútbol realiza el control de peso de diez de sus jugadores cuando regresan de vacaciones. Para tal fin elabora el diagrama de la figura 1.10, en el que destaca con una línea de color verde, el peso que considera ideal para sus jugadores .
Vemos que el jugador C tiene el peso ideal
El jugador A está por encima y el jugador F está por debajo del peso esperado.
Como al preparador físico sólo le interesa saber cuántos kilogramos de más o de menos tiene cada jugador, respecto al peso ideal, decide simplificar la información en la tabla
Jugador | A | B | C | D | E | F | G | H | I | J |
Kg de más o de menos | 3 | +1 | 0 | -4 | +6 | -1 | +2 | -1 | -5 | +5 |
El peso que le hace falta a los jugadores D y F se representa, respectivamente, con los números negativos -4, -1.
El sobrepeso de los jugadores J y G se representa, respectivamente, con los números positivos +5, +2.
PREGUNTA: ¿Cuantos Kilos le sobran en total a los jugadores E y J?
¿Qué son los números enteros?
Para indicar la posición o desplazamiento de un cuerpo, hemos necesitado además de los números naturales, de otros números que se escriben en la recta numérica a la izquierda del cero. Estos números se llaman Enteros Negativos.
Por consiguiente el conjunto de los enteros negativos unido con los números naturales que son los enteros positivos y el cero, constituyen “el conjunto de los números enteros”.
Si llamamos  al conjunto de los enteros positivos y
al conjunto de los enteros positivos y  al conjunto de los enteros negativos, entonces:
al conjunto de los enteros negativos, entonces: 



 .
.
Gráficamente sobre la recta númerica se pueden respresentar así:
PREGUNTA: Suponga que una persona camina 3 pasos a la derecha y luego 2 pasos a la izquierda. ¿A cuántos pasos se encuentra de la posición inicial?
Valor absoluto de un número entero
Hemos visto que los números enteros -2 y + 2 están a la misma distancia de O. El valor 2 se conoce como el valor absoluto de -2 y +2.
En forma análoga, el valor 3 es el valor absolutode los enteros -3 y + 3, puesto que cada uno de estos números se halla a 3 unidades del cero en la recta numérica.
El valor absoluto de un número es la distancia que separa al número del punto  en la recta numérica. Se denota escribiendo el número entre dos barras verticales: I I
en la recta numérica. Se denota escribiendo el número entre dos barras verticales: I I
Sobre la recta numérica podemos verificar que el valor absoluto de cada par de números opuestos es siempre el mismo. Veamos la figura.
PREGUNTA : Analizar la siguiente situación:
Dos automóviles parten de la ciudad A. Uno recorre
+ 40 representa la posición en kilómetros del automóvil que parte hacia el norte respecto al punto de partida y - 40 la posición en kilómetros del automóvil que parte hacia el sur.
Calculemos los valores absolutos de +40 y -40.
I+ 40I = 40
I- 40I = 40
Podemos concluir que :
a) la distancia recorrida por cada automóvil tiene el mismo valor, 40 km.
b)la distancia recorrida por el automovil que va al norte es mayor que la
del automovil que va al sur
c)La distancia del vehículo que va al sur es mayor que la del automovil que
va al norte
Orden en los números enteros
La compañía "petroleos s.a.", adelanta la explotación petrolera de dos pozos. Para seguridad de la explotación rastrea la zona con un avión dotado con radar, como podemo ver en la figura.
¿Que número entero indica la altitud del avión sobre el nivel del suelo?
¿Qué número entero representa la distancia a la que está el pozo 1 del nivel del suelo?
¿A qué distancia se encuentra el pozo 2 del nivel del suelo?
¿Cuál de los pozos se encuentra a mayor profundidad?
Entre los números de las altitudes que observamos en la figura, podemos establecer relaciones como:
Al comparar enteros en una recta númerica vertical, es mayor el entero que está más arriba.
Ahora, ubiquemos sobre una recta numérica horizontal la caseta de materiales, la torre 1 y la torre 2, respecto al operario que se halla justo debajo del avión.
En la recta horizontal de la figura anterior, observemos estas situaciones:
a) La torre 1 se encuentra a la derecha de la caseta de materiales. El entero -1500 que representa la ubicación de la torre 1, es mayor que el entero -2000 que representa la ubicación de la caseta.
Podemos escribir: -1500 > -2000.
Al comparar dos números enteros ubicándolos en una recta númerica horizontal, es mayor aquel número entero que se encuentra a la derecha del otro.
Al comparar dos números enteros, en general, podemos afirmar que:
- Si un número es positivo y el otro negativo, el número entero negativo es menor.
- Si los dos números son positivos, es mayor aquel que se ubica a la derecha del otro en la recta númerica.
- Si los dos números son negativos, es menor el número que esté a mayor distancia del cero.
NOTA: Se llaman positivos los desplazamientos hacia la derecha y negativos deplazamientos hacia la izquierda.
PREGUNTA: ¿Es cierto que -5 < +2?
El plano cartesiano
El sistema de coordenadas cartesianas es aquel formado por dos rectas númericas, una vertical y una horizontal, que se cortan en un punto llamado origen. La recta horizontal es llamada eje de las abcisas o eje de las ( x ); y la recta vertical es llamada eje de las ordenadas o eje de las ( y ).
En el plano cartesiano se pueden encontrar parejas de números llamados coordenadas que se forman con un valor para “x” y un valor para “y”. (x, y).
Ejemplo: Ubicar las siguientes coordenadas en el plano cartesiano: (-3,2); (2,1); (1,-2); (-2,-2).
PREGUNTA: En un plano cartesiano lo mas recomendable a la hora de ubicar un punto es:
a) Ubicar primero el valor de la variable x y después el
de la variable y
b) Ninguna de las anteriores.
c) Ubicar los valores de la variables x y y al
mismo tiempo.
d) Ubicar primero el valor de la variable y y
después el de la variable x
ADICIÓN DE NÚMEROS
ENTEROS
Regla para encontrar la suma de dos números enteros de igual signo:
La suma de dos números enteros de igual signo se obtiene adicionando sus
valores absolutos y escribiéndole al resultado, el signo de los números.
Ejemplo:
(+2) + (+3) = |+2| + |+3| = 2 + 3 = + 5
(-3) + (-1) = |-3| + |-1| = 3 + 1 = - 4
Regla para encontrar la suma de dos números enteros de
diferente signo:
La suma de dos números enteros de diferente signo se
obtiene restando sus valores absolutos (el mayor del menor), y colocándole al
resultado el signo del número que tenga mayor valor absoluto.
Ejemplo:
(-6) + (+2) = |-6| + |+2| = 6 - 2 = - 4
(+5) + (-3) = |+5| + |-3| = 5 - 3 = + 2
PREGUNTA: ¿(-3) + (+2) = ?
a)5 b) -1 c) 1
Sustracción de números enteros.
Recordemos que la sustracción es la operación inversa a la adición.
Si sabemos que (+7) + (+3) = (+10), entonces podemos afirmar que (+10) –
(+3) = (+7).
Si (-5) + (-9) = (-14).
¿Cómo encuentras la diferencia entre dos números enteros?
La sustracción de números enteros se presenta cuando los números son de
diferente signo. Para desarrollar ésta operación debemos seguir los siguientes
pasos:
1. Observar cuál es el mayor de los números y colocar el signo que éste
tenga.
2. Tomar el número menor y restarselo al mayor.
Ejemplo:
(+2) - (+3) = +2 -3
1. Signo del mayor es -
2. Restamos el menor del mayor (3-2)=1
y ordenamos:
(+2) - (+3) = +2 -3 = -1
PREGUNTA: (-3) - (-5) = +2. Falso o verdadero
a) falso b) verdadero
Propiedades de la adición y la sustracción
Claudia tiene que realizar esta operación:
(-145) + (+39) + (-246) + (+1) + (+145) +
(+46)
Para hallar el resultado de esta adición
Claudia sigue el procedimiento que se muestra a continuación.
(-145) + (+39) + (-246) + (+1) + (+145) + (+46) = “Usa el
hecho de que todo número sumado con su opuesto es cero”
(+39) + (+1) + (+46) + (-246) = “cambia el
orden de los sumandos pues sabe que esto no altera el resultado.
[(+39) + (+1)] + [(+46) + (-246)] = Agrupa
las operaciones por pares.
(+40) + (-200) = (-160)
En efecto, la adición de números enteros que cumple las siguientes propiedades.
|
Propiedades de la adición de números
enteros |
||
|
Clausurativa |
(-8) + (-19) = (-27) (+47) + (-18) = (+29) |
La suma obtenida al adicionar números enteros es un número enero. |
|
Conmutativa |
(-67) + (+89) = (+22) (+89) + (-67) = (+22) |
En toda adición el orden de los sumandos no altera la suma. |
|
Asociativa |
(-14) + (+24) + (-5) = [(-14) + (+24)] + (-5) = (-14) + [(+24) + (-5)] (+10)+(-5)=(-14)+(+19) (+5) = (+5) |
Al asociar dos o más sumandos de una adición, en distinto orden, la suma
no se altera. |
|
Propiedad del opuesto aditivo. |
(+6) + (-6) = 0 (+104) + (-104) = 0 |
Todo número entero adicionado con su opuesto aditivo da como resultado
cero. |
La sustracción no cumple con algunas de las propiedades anteriores. Veamos qué pasa con unas de ellas.
Efectuemos las siguientes operaciones.
|
a. (+6) – (+3) = (+3) |
b. (+3) – (+6) = (-3) |
Como el resultado en a. es
diferente al resultado en b., comprobamos que la sustracción
no es conmutativa.
¿La sustracción de números enteros es
asociativa?
Hallemos el resultado de (+23) – (+18) –
(+8).
¿Es lo mismo (+23) – [(+18) – (+8)] que
[(+23) – (18)] – (+8)?
|
a. (+23) – [(+18) – (+8)] (+23) – (+10) = (+13) |
b. [(+23) – (18)] – (+8) (+5) – (+89 = (-3) |
Como en ambos casos el resultado es
diferente, podemos afirmar que la sustracción no cumple la propiedad
asociativa. Al efectuar sustracciones de tres o más términos debemos operar en el
mismo orden en que aparecen.
¿Qué sucede si sustraemos a un número
entero su opuesto aditivo?
Veamos:
(+14) – (-14) = (+14) + (14) = (+28)
(-5) – (+5) = (-5) + (-5) = (-10)
Como el resultado obtenido no es cero, entonces la sustracción no cumple la propiedad del opuesto aditivo.
¿La sustracción de números enteros es
modulativa?
Resolvamos:
|
(-19) -0 = (-19) |
0 – (-133) = (+133) |
|
(+15) – 0 = (+15) |
0 – (+150) = (-150) |
|
(-2) – 0 = (-2) |
0 – (-12) = (+12) |
Comparando ambas columnas comprobamos que la sustracción cumple la
propiedad modulativa solamente cuando el cero (0) se encuentra como sustraendo.
PREGUNTA: (-6+4)+2 = -6+(4+2)
¿Que propiedad se utilizó?
a) Conmutativa. b)Ninguna de las anteriores. c) Clausurativa. d)Asociativa
Potenciación
de números enteros
Alejandra desea descifrar este acertijo: cuatro hombres, cada uno con cuatro hijos, cada hijo con cuatro gatas, cada gata con cuatro gaticos, ¿Cuántos gaticos son?
Ella recuerda lo aprendido en grados anteriores acerca de la potenciación.
La potenciación es el producto de factores iguales.
En la potenciación identificamos los siguientes términos:
En los números enteros la base a puede ser positiva o negativa. Veamos algunos ejemplos.
83 = 8 * 8 * 8 = 512
(-6)4 = (-6) * (-6) * (-6) * (-6) = 1296
(-6)3 = (-6) * (-6) * (-6) = -216
La potencia de un número entero es negativa si la base es negativa y el exponente es impar. En los demás casos es positiva.
La tabla nos muestra las propiedades de la potenciación.
PROPIEDADES DE LA POTENCIACIÓN | ||
NOMBRE | EJEMPLO | GENERALIZACIÓN |
Producto de potencias con bases iguales | ||
|
| |
Potencia de una potencia | ||
Potencia de un producto | ||
Todo número distinto de cero, que tenga como exponente a cero, es igual a 1.
Todo número que tenga como exponente a uno, es igual al mismo número.
Radicación
de números enteros
La radicación es una operación inversa de la potenciación.
En el siguiente ejercicio se puede asegurar que ![\sqrt[3]{8} = 2 \sqrt[3]{8} = 2](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/aae2ac845a729da53b6a3a79cc4458ae.gif) , porque 23 = 8. De la misma forma tenemos
, porque 23 = 8. De la misma forma tenemos ![\sqrt[3]{-8} = -2 \sqrt[3]{-8} = -2](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e35127b50d2299061c129f4a280158b4.gif) , porque (-2)3 = (-8).
, porque (-2)3 = (-8).
En la radicación se diferencian los siguientes términos:
La radicación permite encontrar la base de una potencia.
Veamos la equivalencia en los siguientes ejemplos.
No siempre es posible expresar la raíz de un número entero con un número entero. Por ejemplo, al hallar ![\sqrt[2]{11} \sqrt[2]{11}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/7316604b947cf0c4b335f053ba47a801.gif) , el resultado que se obtiene no es un número entero; igual sucede con
, el resultado que se obtiene no es un número entero; igual sucede con ![\sqrt[2]{-4} \sqrt[2]{-4}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/ae8758f6d062ce7a5dfb141a8527d359.gif) , pues no hay ningún número entero que cumpla ¿?2 = (-4).
, pues no hay ningún número entero que cumpla ¿?2 = (-4).
Para representar la raíz cuadrada de un número escribiremos sólo el signo radical, así: ![\sqrt[2]{25} = \sqrt{25} \sqrt[2]{25} = \sqrt{25}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/845d343dd7dfbd3a07ee71bfd3f3a89e.gif)
En la radicación se cumple:
Si la cantidad del subradical es negativa y el índice es impar, la raíz es negativa.
- Si la cantidad subradical es negativa y el índice es par, la raíz no es un número entero.
Propiedades de las raíces:
1) La potencia de una raíz es igual a la raíz de la potencia:
Ejemplo 1:
2) La raíz del producto de varios factores es igual al producto de las raíces de cada factor:
Ejemplo 2:
3) La raíz enésima de un cociente es igual al cociente de las raices enésimas de los respectivos valores:
Ejemplo 3:
Números Racionales
Número racional es el que se puede expresar como cociente de dos números enteros, es decir, en forma de fracción. Los números enteros son racionales, pues se pueden expresar como cociente de ellos mismos por la unidad: a = a/1.
Los números racionales no enteros se llaman fraccionarios. El conjunto de todos los números racionales se designa por Q.
Así como en el conjunto Z de los números enteros cada número tiene un siguiente (el siguiente al 7 es el 8, el siguiente al -5 es el -4), no pasa lo mismo con los racionales, pues entre cada dos números racionales existen infinitos números.
Q= { m/n , m Z, n Z, n =0 }
Los números racionales pueden sumarse, restarse, multiplicarse y dividirse y el resultado es un número racional.
Números
Racionales
En el curso de Sara 4 de cada 9 niños toman jugo de naranja al desayuno. Si hay 36 alumnos, ¿Cuántos toman jugo de naranja?
Para saber el total de niños que toma jugo de naranja, buscamos una fracción equivalente a  :
:
Decir que 4 de cada 9 niños toman jugo equivale a decir que de 36 alumnos que hay en el curso, 16 toman jugo de naranja al desayuno.
En ocasiones como estas, para solucionar situaciones con números fraccionarios, necesitamos encontrar fracciones equivalentes.
Dos fracciones  y
y 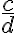 son equivalentes si a*d = c*b.
son equivalentes si a*d = c*b.
Para obtener fracciones equivalentes hacemos uso de los procesos de amplificación y simplificación.
Ejemplo:
Amplifiquemos por 4 la fracción 
Las fracciones  y
y  son equivalentes.
son equivalentes.
El proceso de amplificar o complificar una fracción consiste en multiplicar tanto el númerador como el denominador por un mismo número natural distinto de cero.
Simplifiquenos la fracción  hasta donde sea posible.
hasta donde sea posible.
La fracción  puede seguir simplicándose. Veamos:
puede seguir simplicándose. Veamos:
La fracción 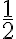 es una fracción irreducible y es equivalente a
es una fracción irreducible y es equivalente a  , es decir:
, es decir:  .
.
El proceso de simplificar una fracción consiste en dividir el númerador y el denominador por un divisor común a ambos.
Cuando una fracción no puede simplificarse, la llamamos fracción irreductible.
Podemos agrupar las fracciones equivalentes a una fracción dada, en un conjunto. Por ejemplo, las fracciones equivalentes a  son:
son:
 . El conjunto formado por una fracción y todos sus equivalentes es una clase. Cada clase recibe el nombre de número racional.
. El conjunto formado por una fracción y todos sus equivalentes es una clase. Cada clase recibe el nombre de número racional.
Se acostumbra tomar como representante de cada clase la fracción irreductible, por ejemplo, el conjunto  =
= 
Al conjunto de todas las clases de fracciones equivalentes lo llamaremos conjunto de los números racionales, el cual se denota 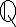 .
.
Al igual que los enteros , los números racionales se pueden clasificar en dos grandes conjuntos, teniendo en cuenta un punto de referencia.
Si se asigna el número cero al punto de referencia, tendríamos que los racionales positivos a la derecha de 0 y los racionales negativos a la izquierda de él.
Orden en los racionales
¿Cómo hacemos para saber cuándo un racionale es menor que otro? Por ejemplo, si tenemos los racionales  y
y  , podemos saber cuál de los dos es menor, amplificando cada uno para obtener fracciones equivalentes con denominador común.
, podemos saber cuál de los dos es menor, amplificando cada uno para obtener fracciones equivalentes con denominador común.
Comparamos luego los númeradores. Como -12 < -10, entonces  . Por consiguiente,
. Por consiguiente, 
Para ordenar números racionales se buscan racionales equivalentes a los dados, que tengan el mismo denominador; luego, se ordenan teniendo en cuenta el orden de los numeradores.
PREGUNTA: ¿ La fracción 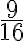 es mayor que
es mayor que  ?
?
ADICIÓN Y SUSTRACCIÓN DE NÚMEROS RACIONALES
La Sustracción es un caso particular de suma, puesto que restar dos números racionales significa sumar uno al opuesto del otro; si consideramos las fracciones  y
y 
Teniendo en cuenta que si
es mayor que
, la fracción resultante será negativa.
Para adicionar o sustraer racionales expresados en forma de fracción, deben tenerse en cuenta dos casos, según que las fracciones tengan igual o distinto denominador.
1) Para sumar o restar fracciones de igual denominador se suman o restan los numeradores y se mantiene inalterado el denominador; para las fracciones: 
EJEMPLO 1:
2) Para sumar fracciones que tienen distinto denominador, se efectua el siguiente proceso:
EJEMPLO 2:
para sumar o restar varias fracciones se procede de la siguiente manera:
Se tiene:
Se busca el mínimo común múltiplo (m.c.m) de los denominadores de las fracciones.
El m.c.m se saca multiplicando de los factores en común el de mayor exponente y de los factores no comunes, todos:
Una vez encontrado el m.c.m, el mismo pasa a ser DENOMINADOR COMÚN entre las fracciones a sumar y sus numeradores respectivos se obtienen dividiendo el denominador común por el denominador que se tenía antes y multiplicando este resultado por el denominador.
Entonces quedaría así las fracciones:
NOTA:
Para sacar el denominador común entre dos o más denominadores sin buscar el m.c.m entre los mismos se opera de la siguiente manera:
1) Si el número más grande de los denominadores es Múltiplo común de todos los denominadores, entonces ése es el denominador común.
EJEMPLO 3:
2) Si el número más grande NO ES MÚLTIPLO de todos los denominadores, se multiplica éste con los denominadores que no sean divisores del mismo.
EJEMPLO 4:
PROPIEDADES DE LA ADICIÓN
EJEMPLO 5:
Neutro aditivo, esto es: Para cualquier racional  se cumple que
se cumple que 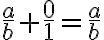 entonces
entonces  es el neutro aditivo.
es el neutro aditivo.
EJEMPLO 6:
Inverso aditivo, esto es: Cada número racional  tiene un inverso aditivo
tiene un inverso aditivo  tal que
tal que 
EJEMPLO 7:
PREGUNTA:  a) 14/4 b) 13/4 c) 14/3 d) 13/3
a) 14/4 b) 13/4 c) 14/3 d) 13/3
Multiplicación
y división de racionales
Para hallar el producto de números racionales multiplicamos los numeradores y denominadores de las fracciones dadas respectivamente.
Ejemplo:
Propiedades de la multiplicación de racionales.
Es invertiva, cada número racional  tiene un inverso multiplicativo con excepción del 0, tal que
tiene un inverso multiplicativo con excepción del 0, tal que 
Es anulativa, esto es: Al multiplicar todo número racional por cero el producto siempre es cero
El producto que se obtiene al multiplicar cualquier número racional por 1 es ese mismo número racional.
La multiplicación se distribuye en la suma, esto es: 
Para Dividir dos números racionales multiplicamos el dividiendo por el recíproco del divisor.
Todo número racional que tenga numerador distinto de cero tiene recíproco o inverso.
El recíproco de un número racional  es
es 
De esa forma tenemos que:
PREGUNTA: a) -139/20 b) -141/2 0 c) 141 /20 d) 139/20
a) -139/20 b) -141/2 0 c) 141 /20 d) 139/20
Potencias y raíces de números racionales
La multiplicación de factores racionales iguales se expresa como una potencia.
Expresemos como potencia el producto 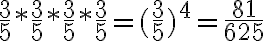
 ;
;  que es el racional que se repite como factor es la base, 4 es ele xponente e indica las veces que se repite la base como factor.
que es el racional que se repite como factor es la base, 4 es ele xponente e indica las veces que se repite la base como factor.
 son formas de expresar la potencia.
son formas de expresar la potencia.
Cuando el exponente es impar y la base negativa, la potencia es negativa. La potenciación cumple las siguientes propiedades:
Raíces enésimas de números racionales
La raíz enésima del racional  es el racional
es el racional 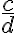 tal que
tal que  .
.
Los términos de la radicación son:
NOTA:
- Si el índice del radical es impar, se puede hallar la raíz de un racional negativo.
- Si el índice es pár, sólo es posible hallar las raíces de racionales positivos, las cuales son positivas.
Propiedad de la radicación:
1) Hallar la raíz enésima de un racional equivale a hallar la raíz enésima de cada uno de sus términos (numerador y denominador).
Ejemplo:
Representación decimal de los racionales
 son racionales cuyos denominadores son potencias de diez, que también puede expresarse como 0.1 y 0.01, respectivamente. Estos números reciben el nombre de racionales decimales. Son ejemplos de racionales decimales los siguientes:
son racionales cuyos denominadores son potencias de diez, que también puede expresarse como 0.1 y 0.01, respectivamente. Estos números reciben el nombre de racionales decimales. Son ejemplos de racionales decimales los siguientes:  ,
,  .
.
Trasformando estos números en decimales obtenemos:
Rrecordemos que el punto separa la parte entera de la parte decimal.
Si queremos escribir un número fraccionario en forma decimal, bastará con dividir el numerador por el denominador.
En la división del numerador entre el denominador da como residuo cero; estos decimales se llaman decimales exactos o finitos. Sin embargo no siempre se da esta situación.
Ejemplo 2:
Encontremos la expresión decimal de  .
.
En el ejemplo anterior los residuos se repiten periódicamente, eso hace que las cifras del cociente también lo hagan. De esta forma obtenemos un número decimal periódico, es decir un número decimal que contiene en su parte decimal un dígito o grupo de dígitos que se repiten indefinidamente.
Al convertir un número racional a decimal se puede obtener un decimal exacto o un decimal periódico. El período es el conjunto de cifras del cociente que se repiten en el mismo orden.
El periodo de la expresión decimal  es 72. Se acostumbra indicar el periódo en un decimal así:
es 72. Se acostumbra indicar el periódo en un decimal así:  .
.
Números como 1.4142135..., 2.020020002..., 3.14159263359..., no pertenecen al conjunto de los números racionales. Reciben el nombre de decimales no periódicos.
Conversión de decimales exactos en racionales
Si se tiene un decimal exacto, podemos encontrar el número racional que lo originó.
Ejemplo:
El número racional  lo hemos expresado como 1.75. Ahora, encontremos el número racional que origina la expresión 1.75.
lo hemos expresado como 1.75. Ahora, encontremos el número racional que origina la expresión 1.75.
 . Al simplificar por 25 tenemos
. Al simplificar por 25 tenemos 
Esta fracción es irreducible.
Para convertir un decimal exacto en racional, se escribe como numerador el número decimal sin punto, y como denominador la potencia de diez con tantos ceros como cifras decimales tenga le número. Luego se simplifica el racional, si es posible.
Operaciones con números decimales.
Adición y sustracción.
Para adixionar y sustraer decimales se procede como si se tratase de enteros, teniendo en cuenta que el punto decimal queda siempre en la misma columna.
Para realizar una sustracción los términos deben tenr la misma cantidad de cifras decimales; de no ser así, se completarán colocando ceros.
Ejemplo:
Resolvamos, -5.03 + (-0.198)
Multiplicación de decimales
La multiplicación de números decimales se realiza como la de enteros. Para saber el número de cifras del producto, se cuenta el número de cifras de los factores.
División de números decimales
Para dividir números decimales se multiplican el dividiendo y el divisor por la misma potancia de 10, de modo que se convierta en enteros. Se expresa la división como una fracción y se simplifica, si es posible, o se divide el numerador entre el denominador.
Ejemplo:
Dividamos, -8.043 entre 0.21
Multiplicando por 1000 ambos términos tenemos:
-8.043 * 1000 = -8043
0.21 * 1000 = 210
PREGUNTA: ¿ a) 0.19 b) 190 c) 1.90 d) 19
a) 0.19 b) 190 c) 1.90 d) 19
ECUACIONES
En mátematicas es frecuente encontrar expresiones como:
 ;
;  ;
;  . Esta clase de expresiones recibe el nombre de igualdad.
. Esta clase de expresiones recibe el nombre de igualdad.
Toda igualdad consta de dos miembros:
Veamos lo que sucede con una igualdad cuando adicionamos o sustraemos el mismo número racional en ambos miembros de ella.
- Adicionamos 4: 18 +2 + 4 = 15 + 5 + 4
- Sustraemos 7: 18 + 2 -7 = 15 + 5 -7
Si en ambos miembros de una igualdad adicionamos, sustraemos o multiplicamos por el mismo número, la igualdad se conserva. Lo mismo sucede si dividimos ambos miembros por un mismo número diferente de cero.
Esta propiedad que se aplica a las igualdades recibe el nombre de propiedad uniforme de la adición, sustracción, multiplicación y división.
Si en una igualdad se encuentra un término desconocido, la igualdad se llama ecuación.
Son ejemplos de ecuaciones:
a + 3 = -17
5x + 9 = 10
Plantear ecuaciones es una estrategia que se usa para la solución de problemas.
Ejemplo:
Apliquemos la propiedad uniforme sumando el opuesto de 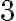
a + 3 + (-3) = -17 + (-3)
Asociamos: a + [3 + (-3)] = -17 + (-3)
Utilicemos la propiedad del opuesto aditivo:
a + 0 = -17 + (-3)
Continuamos con la propiedad modulativa de la adición:
a = -17 + (-3)
Por último hallemos la suma:
Comprobemos que ese valor de a hace verdadera la ecuación:
- 20 + 3 = - 17
Una de las utilidades de plantear ecuaciones es la de saber cuál es la fracción que genera un decimal periódico. Para saberlo, seguimos el proceso que se ilustra a continuación con el siguiente ejemplo:
Encontrar la fracción que genera la expresión decimal 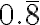
Multiplicamos la expresión por 
Sustraemos de la igualdad (2) la igualdad (1).
Despejando el valor de a obtenemos:
La fracción que genera una expresión decimal periódica se llama fracción generatriz.
En el anterior ejemplo, la fracción generatriz de  es
es  .
.
PREGUNTA: Resuelvo la ecuación: 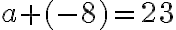
a) a= -15 b) a= 31 c) a= 15
VIDEO EXPRESIONES CON RACIONALES
Variación
proporcional directa
Analicemos las situaciones que se presentan a continuación:
a. En su tienda de víveres, Camilo relaciona en una tabla el peso (en kilogramos) del azúcar y el precio correspondiente. Veamos la tabla.
Azúcar | |
Peso Kg. | Precio $ |
1 | 900 |
2 | 1800 |
3 | 2700 |
4 | 3600 |
5 | 4500 |
Al comparar el número de kilos de azúcar y el precio en la tabla, deducimos que cuanto mayor es el peso en kilogramos de azúcar, mayor es el precio.
b. Un automóvil recorre
¿Qué sucede con la distancia recorrida si el viaje dura menos tiempo?
En estos dos ejemplos, magnitudes como el peso del azúcar y el precio que se paga son dependientes. El tiempo de viaje y la distancia recorrida también lo son.
Dos magnitudes son dependientes una de otra, cuando al cambiar una de ellas la otra también cambia.
Recordemos que cuando comparamos magnitudes homogéneas (de la misma especie), podemos establecer razones.
En la primera situación, por ejemplo, es posible determinar algunas razones entre los kilogramos de azúcar, para compararlas con las razones entre los precios correspondientes.
La razón 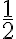 es equivalente a la razón
es equivalente a la razón  y la razón
y la razón 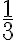 es equivalente a la razón
es equivalente a la razón 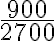
Otra forma de estudiar la tabla del azúcar, consiste en relacionar las magnitudes de diferente tipo. Encontremos algunos cocientes entre el precio del azúcar y el peso correspondiente en kilogramos.
El cociente entre pares de valores de las magnitudes heterogéneas (de diferente especie), que depende una de la otra, a veces es constante.
En la primera situación la constante de proporcionalidad es 900 ya que
Cuando el cociente entre dos magnitudes es constante, decimos que las magnitudes son directamente proporcionales. Este cociente se denomina constante de proporcionalidad.
Representación gráfica de la proporcionalidad directa
La variación de una magnitud en forma proporcional a otra se puede representar gráficamente.
Veamos el siguiente ejemplo:
Representemos los pares de valores(peso en kilogramos y precio) de la tabla del azúcar.
Las parejas correspondientes a los valores de magnitudes que son directamente proporcionales, están ubicadas en una recta que pasa por el origen de los ejes coordenados.
PREGUNTA:  ¿Cuál es la constante de proporcionalidad?
¿Cuál es la constante de proporcionalidad?
a) 18/15 b) 2 4/20 c) 12/10 d) 6/5
Ley de proporcionalidad directa
Ya hemos visto que la variación de la proporcionalidad directa se representa en una tabla o en una gráfica.
La información registra directamente proporcional cumple las siguientes reglas:
· Cuando multiplicamos por n el valor de una de las magnitudes, el valor de la otra también aumenta n veces. Por ejemplo, si se duplica una magnitud, la otra también se duplica.
· Igualmente si dividimos por n el valor de una de las magnitudes, el valor de la otra se hace n veces menor.
· El cociente entre cualquier par de valores correspondientes de las magnitudes es un valor constante, que hemos llamado constante de proporcionalidad y se representa por k.
· La representación gráfica de las parejas correspondientes es una línea recta que pasa por el origen del sistema de ejes de coordenadas.
Consideremos nuevamente la situación del ejemplo del azúcar.
¿Cómo logramos obtener el precio de cualquier cantidad de kilogramos de azúcar? Observemos la tabla.
Para obtener el precio de cualquier peso multiplicamos por 900. Este valor también es el valor del cociente: 
Precio = 900 * peso
El factor multiplicativo que es la constante de proporcionalidad nos permite escribir la ley que relaciona la variación directamente proporcional entre dos cantidades. Para nuestro ejemplo, la ley se escribe: Precio = k * peso.
Si representamos con P el precio y con p el peso, entonces tenemos: P = k * p que se lee: “el precio es directamente proporcional al peso”. Como en nuestro caso la constante de proporcionalidad es 900, podemos escribir P = 900 * p.
Si representamos por x “y” y los valores de dos magnitudes directamente proporcionales, se cumple que  = K o y = k * x, siendo k la constante de proporcionalidad.
= K o y = k * x, siendo k la constante de proporcionalidad.
Encontrar la ley de proporcionalidad entre dos magnitudes es otra forma de resolver los problemas.
PREGUNTA: Una llave vierte 12 litros de agua por minuto; ¿cuántos litros verterá en 4 minutos? a) 60 litros b) 48 litros c) 24 litros d) 36 litros
Variación
proporcional inversa
Si una magnitud crece cuando la otra decrece, decimos que una de las magnitudes depende inversamente de la otra.
Cuando el producto de cada par de valores de las magnitudes que se relacionan es constante, decimos que las magnitudes son inversamente proporcionales. El producto constante se llama constante proporcional inversa.
Ejemplo:
En una camioneta se pueden trasportar 280 litros de agua. La tabla muestra algunas posibilidades para transportar el agua, según el número de garrafas que caben y la capacidad de cada una.
Número de garrafas (g) | Capacidad de cada garrafa (l) |
10 | 28 |
20 | 14 |
40 | 7 |
70 | 4 |
140 | 2 |
Determinamos si las magnitudes relacionadas en la tabla son inversamente proporcionales.
Como el producto entre ellas es constante (280), entonces las magnitudes número de garrafas y capacidad de cada garrafa son inversamente proporcionales.
Representación gráfica de la proporcionalidad inversa
Para representar gráficamente la proporcionalidad inversa se procede de la misma forma que para representar la proporcionalidad directa.
Ejemplo:
Representemos gráficamente la relación entre tiempo y velocidad, teniendo en cuenta los datos de la siguiente tabla.
Tiempo (t) horas | Velocidad (v) km/h |
12 | 25 |
15 | 20 |
20 | 15 |
30 | 10 |
50 | 6 |
Las parejas correspondientes a los valores de magnitudes inversamente proporcionales están ubicados sobre una curva que decrece. Esta curva es la representación gráfica de la variación inversa.
Ley de la proporcionalidad inversa
Las magnitudes que son inversamente proporcionales cumplen con las siguientes propiedades:
· El producto de las dos magnitudes que se relacionan es constante. Este producto se llama constante de proporcionalidad inversa y se representa por k.
· Cuando una magnitud crece n veces a la otra magnitud le corresponde n(enésima) parte.
· La representación gráfica de la proporcionalidad inversa es una curva decreciente.
Consideremos las magnitudes velocidad y tiempo. Como ya vimos anteriormente, la velocidad es inversamente proporcional al tiempo.
Si representamos la velocidad con la letra v y el tiempo con la letra t, la ley que modela esta proporcionalidad inversa se expresa como:
v * t = k
Si x "y" y representan valores de dos magnitudes inversamente proporcionales se cumple que: x * y = k o 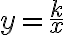 , siendo k la constante de proporcionalidad.
, siendo k la constante de proporcionalidad.
PREGUNTA: Si cinco obreros contruyen una casa en 6 días. ¿Cuántos días tardáran 15 obreros? a) 2 días. b) 5 días. c) 18 días. d) 8 días.
Regla
de tres simple directa
Un problema en el que intervienen dos magnitudes directamente proporcionales y se conocen dos valores de una de ellas y una de la otra, se llama problema de regla de tres simple directa.
Ejemplo:
En el colegio por cada 7 estudiantes varones hay 8 estudiantes mujeres. ¿Cuántos estudiantes son mujeres si en el colegio hay 1050 estudiantes varones?
Solución:
- Como el número de alumnas es proporcional al de alumnos, podemos plantear:
PREGUNTA: En un curso de séptimo, la profesora propone este problema: seis cuadernos iguales tienen un precio de $ 19.200. ¿Cuánto cuestan 15 de esos mismos cuadernos?
a) 47000 b) 48000 c) 50000 d) 49000
Regla
de tres simple inversa
Un problema en el cual se relacionan dos magnitudes inversamente proporcionales y en el que se conocen dos valores de una de ellas y uno de la otra, se llama un problema de regla de tres simple inversa.
Para resolver un problema de tres simple inversa se puede:
- Plantear una proporción que iguale la razón entre los valores de una magnitud y la razón formada con los valores correspondientes, colocados en forma inversa.
- Calcular el término desconocido aplicando procedimientos relacionados con la proporcionalidad inversa.
Ejemplo:
Un grupo de amigos decide comprar la dotación para su equipo deportivo, que vale $ 150.000. Cuando ya han fijado la cuota que deben aportar, dos compañeros más se suman al grupo. Si la cuota fijada inicialmente era de $ 15.000, ¿Cuánto será ahora la cuota de cada uno de los 12 amigos del grupo?
Para resolver este problema, algunos de los amigos proponen las siguientes soluciones:
- Mateo aplicó las propiedades de la proporcionalidad inversa:
Recordemos que cuando dos magnitudes son inversamente proporcionales, al aumentar una de ellas n veces la otra se hace n veces menor.
Cuota $ 15000 * 5 = 75000
6 = 12500
La cuota es $ 12.500
- Margarita resolvió el problema así:
El producto de lo aportado por cada uno y del total de aportantes debe dar el precio de la compra.
# de personas | 10 | 12 |
Cuota | 15000 | ¿? |
Total | 10 * 15000 | 12 * ¿? = 150000 |
Encontramos el valor desconocido en la expresión 12 * ¿? = 150000, concluimos que el valor de la cuota debe ser $12.500
- Juan planteó una proporción así:
Como son más los aportantes y la cantidad de dinero que se va a reunir es la misma, entonces el dinero que aportará cada uno de los doce será menor que $15.000. Por ello se plantea una proporción entre la cuota y el número de amigos así:
Despejando el valor desconocido, obtenemos nuevamente que la cuota de cada uno de los doce amigos es $12.500
PREGUNTA: En una familia compuesta por tres adultos, se hace un mercado que alcanza para 15 días. Para las vacaciones llega de visita una pareja de amigos. ¿Para cuántos días alcanzará el mismo mercado si no cambian ni el número de comidas ni la ración?
a) 10 días b)9 días c)8 días d)3 días
Regla
de tres compuesta
Un problema en el que se relacionan tres o más magnitudes directa o inversamente proporcionales y que requiera encontrar uno de los valores, se llaman un problema de regla de tres compuesta.
Para la resolución de un problema de regla de tres compuesta pueden usarse proporciones o procedimientos asociados a la proporcionalidad directa o inversa, según corresponda.
Ejemplo:
En una dulcería tienen 9 empleados que, trabajando 8 horas, hacen y empacan 150 cajas de dulces. ¿Cuántas horas tardarán 12 empleados en hacer y empacar un pedido de 375 cajas?
- Las tres magnitudes involucradas en el problema son: número de empleados, tiempo y número de cajas de dulces.
- De la lectura del problema podemos deducir que con más empleados tomará menos horas despachar el pedido; de otra parte, para hacer y empacar más dulces se gastarán más horas.
Ahora bien, primero estudiemos la situación cuando no varía el número de empleados. El número de cajas de dulces empacados es directamente proporcional al tiempo necesario para hacerlos y empacarlos.
Luego 9 empleados gastarían 20 horas en hacer y empacar el pedido de 375 cajas.
Ahora, si mantenemos la producción de 375 cajas, el número de empleados es inversamente proporcional al tiempo gastado, por tanto, se tiene la siguiente proporción:
Luego para producir 375 cajas de dulces 12 empleados gastarían 15 horas.
Otra manera de resolver el problema es usar procedimientos asociados a la proporcionalidad directa e inversa, como se muestra a continuación:

PREGUNTA: Nueve grifos abiertos durante 10 horas diarias han consumido una cantidad de agua por valor de 20 US$. Averiguar el precio del vertido de 15 grifos abiertos 12 horas durante los mismos días. a) $60 b)$40 c)$ 30 d)$50
INTERÉS
Los maestros y los alumnos del colegio han organizado un "Banco Estudiantil", con el objeto de acostumbrar a los estudiantes a manejar su dinero correctamente. El banco estudiantil acepta dinero de los alumnos y les reconoce un interés mensual. También otorga préstamos por los cuales cobra un interés mensual.
El interés es una cantidad proporcional a:
- El porcentaje fijado por la junta directiva del banco estudiantil (rata).
- La cantidad de dinero que se deposita (capital).
- El tiempo que permanece consignado el dinero.
Jaime abre una cuenta con $ 10.000. Hallemos cuánto interés recibe en un mes si el banco estipula un porcentaje de 4%.
El porcentaje expresa la razón entre una parte y el todo, que se representa con 100.
El 4% de $10.000 son $400. Jaime recibe $400 de interés mensual.
La cantidad recibida por Jaime al sacar su dinero del banco se llama monto y es la suma del capital que consignó más los intereses.
En una tranbsacción comercial quien recibe el dinero o el bien se llama deudor, quien lo entrega se conoce como acreedor.
El valor del bien o la cantidad total entregada o solicitada se llama capital, préstamo o crédito.
El porcentaje pagado por el uso dle bien o el dinero se llama rata y puede ser diaria, mensual, semestral o anual.
El dinero pagado por el uso de un bien o un capital durante cierto tiempo se llama interés.
Ejemplo:
El titular de una cuenta de ahorros, a la que el banco le reconoce un porcentaje anual de 30%, consigna $102.600.
a) ¿cuánto interés le rinde este capitalen 6 meses?
b) Si mantiene el dinero en el banco durantre dos años, ¿cuánto recibirá al terminar ese período?
c) ¿Por cuánto tiempo debe mantener el dinero en el banco, si cuando lo retire quiere recibir un total de $200.000
Solución:
a) Para calcular el interés producido por el capital en seis meses basta resolver consecutivamente las siguientes situaciones:
$100 generan un interés anual de $30; deseamos saber qué interés anual produce un capital de $102.600
Capital | Interés anual |
100 | 30 |
102600 | ? |
Como las magnitudes capital e interés anual sondirectamente proporcionales, esteblecemos la siguiente proporción:
Luego el interés anual que gana el capital de $102.600 es $30.708
Ahora se calcula el interés que gana el capital de $102.600 en un período de seis meses, teniendo en cuenta que en un año (12 meses) gana $30.780.
Tiempo (meses) | Interés |
12 | 30780 |
6 | ? |
Las magnitude tiempo e interés tambuién son directamente proporcionales, entonces:  , de donde obtenemos: x=$15.390
, de donde obtenemos: x=$15.390
b) Para dar respuesta a la segunda pregunta basta considerar que la rata anual se ha conservado y lo que cambia es el tiempo, por tanto:
Tiempo (en años) | Interés |
1 | 30780 |
2 | ? |
En este caso el interés recibido en un periodo de dos años, resulta ser $61.560 y el monto rcibido será $61.560 + $102.600 = $164.160
c) El ahorrador quiere recibir $200.00 al retiral el ahorro, es decir, quiere ganar de interés: $200.00 - $102.600 = $97.400
De acuerdo con el desarrollo de la parte a., en un año el ahorrador gana $30.780 de interés; ahora se puede plantear la siguiente situación:
Interés | Tiempo (en días) |
$ 30.780 | 360 |
$ 97.400 | T |
Para operaciones comerciales se considera que un año tiene 360 días y un mes tiene 30 días. Como el interés percibido es directamente proporcional al tiempo y se sabe que $30.780 es el interés anual, entonces T = 1139.18 días. Luego para lograr reunir $200.000 debe colocar el capital durante 1140 días ( el banco exige un día más por 0.18 días), es decir, 3 años y 2 meses.
PREGUNTA: Del ejemplo anterior. ¿Cuánto interés le rinde del capital en 18 meses? Si mantiene el dinero en el banco durante 5 años, ¿cuánto recibirá al terminar ese periodo?
a) $46.170 y $ 256.500 b)$46.130 y $ 256.700 c)$46.150 y $ 256.300 d)$46.190 y $ 256.400
LOS
CIMIENTOS DE LA GEOMETRÍA
En geometría hay tres elementos que no pueden definirse, pero que sí se pueden describir y representar. Estos son: punto, plano y recta. Con ellos se construye el mundo geométrico. Cuando vamos a reunirnos con los amigos en un centro comercial, hablamos del punto de encuentro, es decir, del sitio exacto donde nos veremos. En geometría, punto también significa una posición, un sitio exacto. No tiene tamaño, ni dimensión. Se representa por medio de una marca redonda, tan pequeña como sea posible, y se nombra usando alguna letra mayúscula.
Una recta esta conformada por infinitos puntos, uno tras otro, extendiéndose en sectores opuestos. Tiene una dimensión. Se acostumbra nombrarla con dos puntos que estén en la recta o con una letra minúscula: l, n o m.
Por dos puntos sólo se pasa una recta, es decir, dos puntos determinan una recta.
Un plano tiene dos dimensiones y se extiende infinitamente en todas las direcciones y sentidos. Se representa con una figura plana y se nombra con una letra mayúscula, con cuatro letras mayúsculas o utilizando letras del alfabeto griego.
Plano M o ABCD, las flechas indican que le plano se extiende indefinidamente en todas las direcciones y sentidos.
Tres puntos que no están en una misma recta, determinan un plano.
La mesa que vemos en la figura, es un buen modelo físico de estas tres ideas. Una esquina nos da la idea de punto, un borde de la recta y la superficie la de plano.
Con estos tres elementos se construyen las figuras geométricas.
Recordemos algunas definiciones y sus representaciones.
Observemos que un rayo o semirrecta tiene punto inicial y se extiende en un solo sentido infinitamente. Un segmento tiene dos extremos. El punto común de los dos rayos que conforman el ángulo se llama vértice y los rayos son los lados del ángulo. Un ángulo separa el plano en dos regiones; la parte interior al ángulo y la exterior.
En geometría es necesario, en ocasiones, hallar la intersección de dos o más figuras.
La intersección de dos figuras es el conjunto de puntos que están en ambas figuras.
La intersección de dos rectas es un punto y la de los planos es una recta
PREGUNTA: Los lados de un ángulo son conocido tambien como:
RECTAS
PARALELAS Y PERPENDICULARES
Dos rectas son perpendiculares cuando al cortarse o intersecarse forman cuatro ángulos de 90° o ángulos rectos.
En la siguiente gráfica mostraremos cuando dos rectas son perpendiculares teniendo en cuenta la definición dada.

Observe que en esta gráfica las rectas 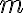 y
y 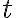 se cortan en un sólo punto, formando los cuatro ángulos de 90°.
se cortan en un sólo punto, formando los cuatro ángulos de 90°.
Dos rectas son paralelas si son coplanares y no se intersecan, en otras palabras, dos rectas son paralelas cuando se encuentran en un mismo plano y no se cortan en en ningún punto.
En la siguiente gráfica se ilustra dos rectas paralelas.

Observe que en esta gráfica las rectas 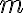 y
y 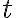 no se cortan en ningún punto.
no se cortan en ningún punto.
Una recta que interseca dos rectas coplanares se denomina transversal, es decir, una recta es transversal cuando corta a dos o mas rectas paralelas en forma diagonal.
En la siguiente gráfica se ilustra un recta transversal.

Observe en esta gráfica que la recta que es transversal es la recta 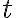 , dado que este interseca las dos rectas paraleleas.
, dado que este interseca las dos rectas paraleleas.
PREGUNTA: Los ángulos que forman dos rectas perpendiculares reciben el nombre de ángulos rectos, conocido por que tienen una medida de:
a)70°. b)90°. c)180°. d)80°
FIGURAS
PLANAS
Triángulo
Un triángulo es la unión de tres segmentos determinados por tres puntos no colineales.
La semirrecta que divide un ángulo en dos ángulos congruentes y tiene por origen el vértice del ángulo, se conoce como bisectriz.
En todo triangulo el punto de intersección de las bisectrices se llama incentro.
Además de las bisectrices, otras líneas del triangulo son las alturas. Una altura de un triangulo es un segmento que va de un vértice a la recta que contiene el lado opuesto y es perpendicular a ésta.
Todo triangulo tiene tres alturas que se intersecan en un solo punto llamado ortocentro.
Una mediana de un triángulo es un segmento que va de un vértice del triángulo al punto medio del lado opuesto.
Cuadriláteros
Un cuadrilátero es un polígono de cuatro lados. Los cuadriláteros pueden clasificarse por las características especiales entre sus lados y ángulos. Estudiaremos dos tipos de cuadriláteros: Paralelogramos y trapecios.
Un paralelogramo es un cuadrilátero con ambos pares de lados opuestos paralelos.
Los ángulos opuestos en un paralelogramo son congruentes.
Los lados opuestos de un paralelogramo son congruentes.
Los paralelogramos se clasifican según las propiedades que tienen sus lados o ángulos.
Otro tipo de cuadrilátero es aquel que tiene exactamente dos lados paralelos. Esa figura se llama trapecio. Sus lados paralelos se llaman bases y cada ángulo con vértice en un extremo de la base se llama ángulo de la base. Un trapecio en el cual los lados no paralelos son congruentes es un trapecio isósceles.
PREGUNTA: ¿Cuál es el nombre del cuadrilatero que tiene exactamente dos lados paraleleos? *Rombo. *Cuadrado. * Ninguna de las anteriores. * Trapecio
CIRCUNFERENCIA
Una circunferencia es el conjunto de todos los puntos coplanares equidistantes de un punto fijo llamado centro.
Definimos medida de un arco de circunferencia como la medida del ángulo central que pasa por los extremos del arco.
Llamaremos punto de tangencia al punto de corte de la circunferencia con la recta tangente.
La tangente a una circunferencia es perpendicular al radio trazado al punto de tangencia.
PREGUNTA: La afirmación, en la circunferencia el diámetro es el doble del radio es:
* La afirmación no está bien definida. * Verdadero.
* Falso
LONGITUD,
PÉRIMETRO, ÁREA
Los objetos tienen magnitudes medibles entre las que están la longitud y la superficie entre otras:
Longitud nos permite decir que tan largo es un objeto.
Superficie que tanta área cubre.
Perímetro es la longitud del contorno de una figura o superficie.
Área es magnitud de medida de la superficie.
En la siguiente tabla podremos observar la forma de pasar de una unidad de medida a otra.
En el siguiente cuadro encuentra áreas y perímetros de algunas figuras:
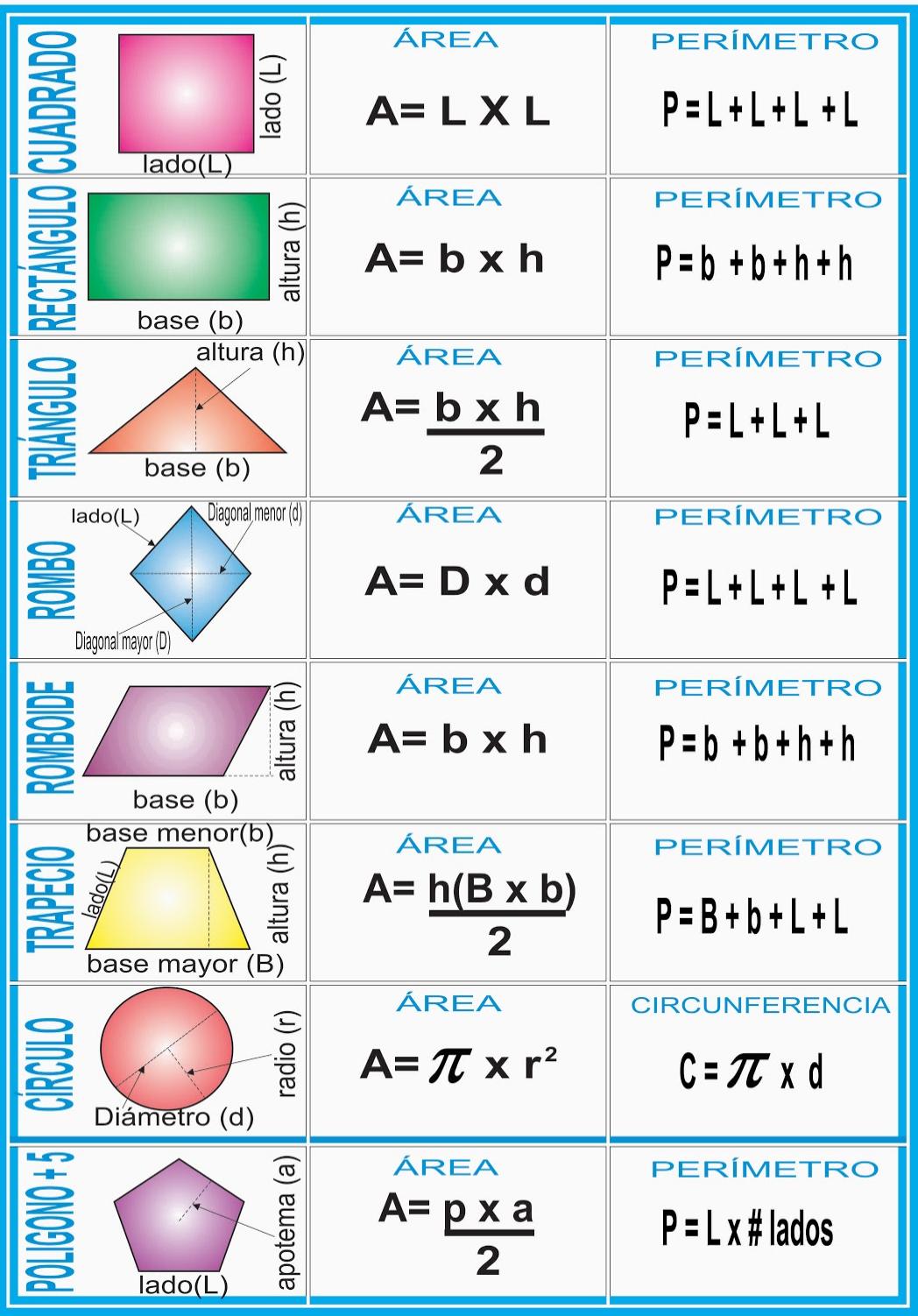
PREGUNTA: Al transformar 2000 metros a kilómetro, el resultado es:
ÁREA DE
FIGURAS PLANAS
El área del rectángulo: Se obtiene hallando el producto de las longitudes del largo y el ancho. 
Ejemplo:
¿Cuál es el área de un rectángulo de dimensiones 7 cm y 3 cm?
El área del cuadrado: Se obtiene hallando el producto de las longitudes de dos de sus lados. 
Ejemplo:
¿Cuál es el área de un cuadrado de 7 cm de lado?
El área de un paralelogramo: Se obtiene calculando el producto de la longitud de un lado llamado base y la altura correspondiente a ese lado. 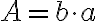
Ejemplo:
¿Cuál es el área del paralelogramo de la figura?
El área de un triangulo: Se halla el producto de la longitud de un lado por la altura correspondiente a ese lado, y el resultado se divide en 2. 
Ejemplo:
¿Calculemos el área del triangulo de la figura?
El área de un trapecio: Hallamos el producto de la suma de las longitudes de los lados paralelos por la altura y dividimos el resultado entre 2. 
Ejemplo:
¿Encontremos el área del trapecio de la figura?
PREGUNTA: ¿Cuál es el área de un paralelogramo de dimensiones de 6 cm y 1 dm?
* 6cm2 * 60cm2
* 600cm2
ÁREA DE POLÍGONOS REGULARES Y DEL
CÍRCULO. TEOREMA DE PITÁGORAS
Un polígono regular es el que tiene todos sus lados congruentes. Todo polígono regular puede descomponerse en triángulos isósceles congruentes. La suma de las áreas de esos triángulos equivale al área de la región poligonal.
El área de una región encerrada por un polígono regular de n lados de longitud l es:
En el siguiente cuadro se puede observar la fórmula de obtener el area de poligonos regulares de más de 4 lados.
Área del círculo
Al aumentar el número de lados de la región poligonal se va aproximando a un círculo. Si consideramos que una circunferencia es un polígono de infinito número de lados, el área del círculo correspondiente se obtiene en forma similar a la de los polígonos regulares.
Imaginemos el círculo dividido en infinito número de triángulos. La altura de cada triangulo corresponde al radio de la circunferencia.
El área de una región encerrada por un círculo es:
El perímetro o longitud de una circunferencia es una magnitud directamente proporcional a su diámetro y se obtiene multiplicando el diámetro por el valor de 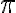 , que corresponde a un número aproximadamente igual a 3.14 o
, que corresponde a un número aproximadamente igual a 3.14 o 
Entonces:
El área del círculo será igual a:
Ejemplo:
Calculemos el perímetro y el área de la región encerrada por una circunferencia de radio 3 cm
Solución
La longitud de la circunferencia es 18.84 cm aprox. El área del circulo corresponde a 28.26 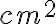 aprox.
aprox.
PREGUNTA: ¿Cuánto mide el radio de un circulo, que tiene de área 
*4.78 cm *3.87 cm *3.78
cm *4.87 cm
VOLUMEN
Y CAPACIDAD
El volumen de un cuerpo es el número de unidades cúbicas que lo componen. Las unidades cúbicas más utilizadas en el sistema internacional de medidas son: metro cúbico, decímetro cúbico y centímetro cúbico.
La siguiente tabla presenta algunas equivalencias de múltiplos y submúltiplos (o divisores) del 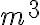
Muy ligada al volumen esta la medida de la capacidad. En matemáticas se define así:
Capacidad es la facultad de los envases huecos para alojar algo. Por ejemplo agua, arena, paquetes, etc.
La capacidad se mide en las mismas unidades que el volumen. También puede medirse en litros o en múltiplos y submúltiplos del litro.
En un recipiente de  cabe 1 litro
cabe 1 litro  de liquido.
de liquido.
Los divisores del litro se obtienen dividiendo de 10 en 10, mientras que los divisores del metro cúbico se obtienen dividiendo de 1000 en 1000.
PREGUNTA: ¿Cuál es el volumen de un cubo de 2 cm de lado?
*10 cm3 *8 cm3 *4
cm3 *6 cm3
CONCEPTOS BÁSICOS DE ESTADÍSTICA
La estadística es el conjunto de procedimientos y técnicas empleadas para recolectar, organizar y analizar datos, los cuales sirven de base para tomar decisiones en las situaciones de incertidumbre que plantean las ciencias sociales o naturales.
ESTADÍSTICA DESCRIPTIVA
La estadística descriptiva se refiere a la recolección, presentación, descripción, análisis e interpretación de una colección de datos que permiten resumir por medio de elementos de información (medidas descriptivas) características de la totalidad de los mismos y llegar a una conclusión sobre la muestra o población que se analiza.
ANÁLISIS ESTADÍSTICO
El análisis estadístico es todo el proceso de organización, procesamiento, reducción e interpretación de datos para realizar inferencias.
DATOS Y VARIABLES
Variables: Es toda característica que varía de un elemento a otro de la población.
Datos: Son medidas o valores de las características susceptibles de observar y contar, se originan por la observación de una o más variables de un grupo de elementos o unidades
CLASIFICACIÓN DE VARIABLES
Categóricas o cualitativas: Son atributos o cualidades que no tienen ningún grado de comparación numérica. Por ejemplo: sexo, estado civil, color de ojos, etc.
Numéricas o cuantitativas: Son características contables o medibles que se expresan numéricamente. Por ejemplo: número de estudiantes, peso, calificaciones, etc.
Las variables cuantitativas pueden ser de dos tipos:
Discretas: Solo pueden tomar ciertos valores aislados en un intervalo. Por ejemplo el tamaño de la población (1,2,3... personas).
Continuas: que pueden tomar cualquier valor en un intervalo. Por ejemplo la estatura de una persona (160cm, 160.1cm, 160.15cm ,etc).
EJERCICIO PRÁCTICO
Clasifiquemos las siguientes características de una población en cualitativas y cuantitativas.
| Familia de un árbol | Color favorito |
| Tipo de hojas | Máximo grosor de un tronco |
| Número de hojas de un libro | Peso |
| Estatura | Puntaje promedio de goles en el campeonato |
| Sueldo mensual de un empleado | Estrato del barrio donde vivo |
| Número de hermanos | Deporte favorito |
| Nombre | Tiempo que tardo en hacer una tarea |
| Sexo |
Algunas características cualitativas son: Color favorito, nombre, deporte favorito, sexo.
Son cuantitativas: Número de hermanos, sueldo mensual de un empleado, estatura, estrato del barrio donde vivo, peso.
El número de hermanos y el estrato de un barrio son características que sólo pueden tomar valores aislados y no pueden tomar algún valor entre dos valores consecutivos.
Por su parte, consumo de agua o luz, estatura y tiempo que tardo en hacer una tarea, son características que pueden tomar muchos valores entre dos de ellos; por ejemplo: la altura de un árbol puede ser 3 m o 4 m, pero valores intermedios como 3,5 m y 3.75 m también pueden corresponder a la altura de un árbol.
Una carecterística cuantitativa que en un rango toma datos aislados de modo que no acepta valores intermedios entre dos consecutivos, se llama cuantitativa discreta. Si se trata de una característica que puede tomar valores entre dos valores consecutivos, se dice que es una variable cuantitativa continua.
PREGUNTA: Teniendo en cuenta que las variables se clasifican en categóricas y numéricas. La numérica se clasifica a su vez en discretas y continuas; se puede concluir que la variable edad es:
REPRESENTACIÓN
DE DATOS
Los datos son colecciones de un número cualquiera de observaciones relacionadas entre si, para que sean útiles se deben organizar de manera que faciliten su análisis, se puedan seleccionar tendencias, describir relaciones, determinar causas y efectos y permitan llegar a conclusiones lógicas y tomar decisiones bien fundamentadas.m Por esa razón es necesario conocer los métodos de organización y representación, cuya finalidad es permitir ver rápidamente todas las características posibles de los datos que se han recolectado.
Representación Tabular:
Presenta las variables y las frecuencias con que los valores de éstas se encuentran presentes en el estudio.
Representación Gráfica :
Se llaman gráficas a las diferentes formas de expresar los datos utilizando los medios de representación que proporciona la geometría.
METODOS DE REPRESENTACIÓN DE DATOS CUANTITATIVOS
Arreglo de Datos: Es una forma de presentar los datos en un arreglo ascendente o descendente.
Ventajas: Describe los valores mínimos y máximos, en él se pueden dividir los datos fácilmente en secciones, permite darse cuenta de los valores que aparecen más de una vez, se puede observar la distancia entre valores consecutivos.
Diagrama de Puntos: Muestra la frecuencia con que aparece cada uno de los valores.
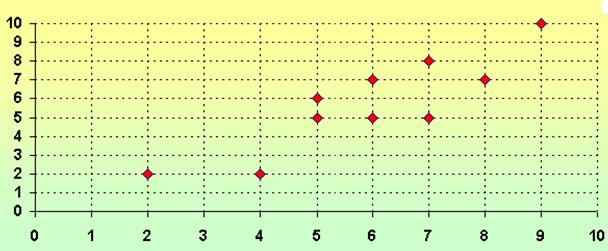
Diagrama de Tallo y Hoja: Es útil para realizar una exploración preliminar del conjunto, genera una imagen adecuada de ellos sin perder información.
Veamos un Ejemplo con los siguientes 15 datos:
35, 36, 38, 40, 42, 42, 44, 45, 45, 47, 48, 49, 50, 50, 50
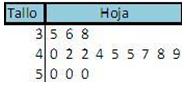
Distribución de Frecuencias: Es una forma de sintetizar los datos y consiste en valerse de una tabla para clasificar los datos según su magnitud, en ella se señala el número de veces que aparece cada uno de los valores. Cuando se dispone de un gran número de valores discretos o cuando las variables son continuas, tiene sentido formar una tabla que presente la distribución de frecuencias de los datos agrupados en intervalos o clases, de igual tamaño si es posible.
Veamos un ejemplo:
Se tienen 5 tipos de árboles y una cantidad determinada de cada uno de ello en un parque natural. Podemos representarlo por medio de una tabla como se muestra a continuación.
Tipo de árbol | No. de árboles |
Acacias | 5 |
Azaleas | 2 |
Cauchos | 3 |
Eucaliptos | 7 |
Pinos | 15 |
Urapanes | 18 |
Definiciones para elaborar tablas de distribución de frecuencias
Rango: Es la diferencia entre el valor mínimo y el valor máximo de los datos que se tienen:
Rango = Dato máximo - Dato mínimo
Clases o intervalos de clase: Grupo de valores que describen una característica. Deben incluir todas las observaciones y ser excluyentes. Los intervalos contienen los límites de clase que son los puntos extremos del intervalo. Se denominan intervalos cerrados, cuando contienen ambos límites e intervalos abiertos si incluyen solo un límite.
Limites Reales: Sirven para mantener la continuidad de las clases, son los valores extremos inferirores y superiores de los datos que se agrupan en una clase.
Anchura o tamaño del intervalo: Es la diferencia entre los límites reales de una clase.
Número de clases: Es el número total de grupos en que se clasifica la información, se recomienda que no sea menor que 5 ni mayor que 15.
Marca de Clase: Es el punto medio del intervalo de clase, se recomienda observar que los puntos medios coincidan con los datos observados para minimizar el error.
Frecuencia: Es el número de veces que aparece un valor.
Frecuencia Acumulada: Indica cuantos casos hay por debajo o arriba de un determinado valor o límite de clase.
Frecuencia Relativa: Indica la proporción que representa la frecuencia de cada intervalo de clase en relación al total, es útil para comparar varias distribuciones con parámetros de referencia uniformes.
Veamos un ejemplo:
Se indagó por el número de hermanos que tienen los 25 alumnos de un curso de grado séptimo. Los resultados se presentan en la siguiente tabla.
No de hermanos | No de alumnos | % de alumnos |
0 | 3 | 12% |
1 | 8 | 32% |
2 | 6 | 24% |
3 | 4 | 16% |
4 | 2 | 8% |
5 | 2 | 8% |
Frecuencia Acumulada Relativa: Indica la proporción de datos que se encuentra por arriba o debajo de cierto valor o límite de clase.
Gráficos de una Distribución de Frecuencias
Los gráficos son útiles porque ponen en relieve y aclaran las tendencias que no se captan fácilmente en la tabla, ayudan a estimar valores con una simple ojeada y brinda una verificación gráfica de la veracidad de las soluciones.
Histograma:
Esta formado por rectángulos cuya base es la amplitud del intervalo y tiene la característica que la superficie que corresponde a las barras es representativa de la cantidad de casos o frecuencia de cada tramo de valores.
Veamos el histograma que representa la tabla de frecuencias de los árboles en el parque natural:
Polígono de Frecuencias
Se puede obtener uniendo cada punto medio (marca de clase) de los rectángulos del histograma con líneas rectas, teniendo cuidado de agregar al inicio y al final marcas de clase adicionales, con el objeto de asegurar la igualdad del áreas.

Diagramas circulares:
Son utilizados en aquellos casos donde nos interesa no sólo mostrar el número de veces que se da una característica o atributo de manera tabular sino más bien de manera gráfica, de tal manera que se pueda visualizar mejor la proporción en que aparece esa característica respecto del total.
Veamos la preferencia n la práctica de deportes de cierta población:
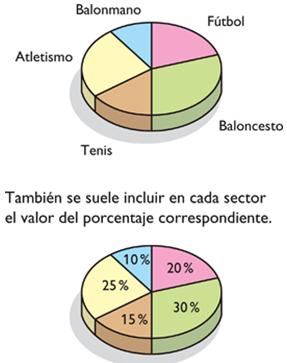
Ejercicio práctico:
En la clase de educación física el maestro tomó la medida de la estatura de los alumnos de grado séptimo; él apuntó los datos aproximando en centímetros, así: si medía entre 154.1 cm y 154.4 cm, anotaba 154; pero si medía entre 154.5 y 154.9, anotaba 155 cm.
En una primera presentación el maestro agrupó los datos como se dan en la tabla.
Estatura en cm | 146 | 148 | 150 | 152 | 153 | 155 | 157 | 161 | 163 | 166 | 168 | 170 |
No de alumnos | 1 | 2 | 2 | 3 | 5 | 9 | 7 | 4 | 3 | 2 | 1 | 1 |
Como la estatura es una característica continua, es posible agrupar los datos, considerar intervalos de cinco centímetros y reunir, en cada uno, los alumnos cuya estatura está en ese intervalo, así:
Como el rango de estatura está entre 146 cm y 170 cm, podemos agrupar en 5 intervalos de 5 cm cada uno. El maestro agrupa así:
En el primer intervalo incluye a los estudiantes con 145,5 cm o más hasta 150,4 cm; en el segundo a los que tiene entre 150,5 cm y 155,4 cm; etc., así obtiene la siguente tabla.
Estatura | No de alumnos |
146 - 150 | 5 |
151 - 155 | 17 |
156 - 160 | 7 |
161 - 165 | 7 |
166 - 170 | 4 |
De acuerdo con la tabla el maestro observa que 17 de sus alumnos tienen una estatura superior a 150 cm hasta 155 cm, y que los alumnos con estatura superior a 165 cm hasta 170 cm son apenas 4.
La gráfica correspondiente es:
PREGUNTA: Se recopiló información sobre el peso de 40 alumnos de grado séptimo; los resultados son agrupados en una tabla, usando intervalos de 7 kg cada uno. ¿Qué tipo de representación es la más adecuada?
Peso de los alumnos | No de alumnnos |
36 - 42 | 7 |
43 - 49 | 11 |
50 - 56 | 8 |
57 - 63 | 9 |
64 - 70 | 5 |
* El diagrama de barras y el diagrama lineal * El diagrama circular y el diagrama lineal
* El histograma y el diagrama circular * El histograma y el poligono de frecuencias
MEDIDAS DE TENDENCIA CENTRAL:
MEDIA, MEDIANA Y MODA
MEDIDAS DESCRIPTIVAS
Con estas medidas se persigue reducir en pocas cifras significativas el conjunto de observaciones de una variable y describir con ellas ciertas características de los conjuntos, logrando una comparación más precisa de los datos que la que se puede conseguir con tablas y gráficas.
MEDIDAS DE TENDENCIA CENTRAL - PROMEDIOS
Los promedios son una medida de posición que dan una descripción compacta de como están centrados los datos y una visualización más clara del nivel que alcanza la variable, pueden servir de base para medir o evaluar valores extremos o "raros" y brinda mayor facilidad para efectuar comparaciones.
MEDIA ARITMÉTICA
Es el valor alrededor del cual se agrupan los demás valores de la variable.
Para datos no agrupados utilizaremos:
Donde:
 es la suma de todos los datos (Sumar una a uno los datos)
es la suma de todos los datos (Sumar una a uno los datos)
n es el numero de datos (se debe contar cuantos datos se tienen)
Para datos agrupados utilizaremos:
Donde:
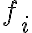 es la frecuencia de cada dato (las veces que se repite en el conjunto de datos que se tienen).
es la frecuencia de cada dato (las veces que se repite en el conjunto de datos que se tienen).
 es la marca de clase para cada intervalo.
es la marca de clase para cada intervalo.
 Es la multiplicacion de cada dato por la frecuencia o veces que se repite en el conjunto de datos y finalmente se suman los resultados
Es la multiplicacion de cada dato por la frecuencia o veces que se repite en el conjunto de datos y finalmente se suman los resultados
LA MODA
Es el valor de un conjunto de datos que ocurre más frecuentemente, se considera como el valor más típico de una serie de datos. Se presenta en datos no agrupados.
Para datos agrupados se define como Clase Modal el intervalo que tiene más frecuencia.
La moda puede no existir o no ser única, las distribuciones que presentan dos o más máximos relativos se designan de modo general como bimodales (2 modas)o multimodales (varias modas).
LA MEDIANA
Es el valor de la observación que ocupa la posición central de un conjunto de datos ordenados según su magnitud. Es el valor medio o la media aritmética de los valores medios. La mediana es un valor de la variable que deja por debajo de él un número de casos igual al que deja por arriba.
Geométricamente la mediana es el valor de la variable que corresponde a la vertical que divide al histograma en dos áreas iguales.
Cuando determinados valores de un conjunto de observaciones son muy grandes o pequeños con respecto a los demás, entonces la media aritmética se puede distorsionar y perder su carácter representativo, en esos casos es conveniente utilizar la mediana como medida de tendencia central.
EJERCICIO PRACTICO
Un profesor de matemáticas anotó la estatura de los estudiantes de su clase. Esta es la lista que presentó:
Se desea deteminar las medidas de tendencia central MEDIA ARITMETICA, MEDIANA Y MODA.
Primero realizaremos una tabla de frecuencias:
TABLA A
151 | 2 |
152 | 3 |
153 | 4 |
154 | 7 |
155 | 9 |
156 | 6 |
157 | 2 |
158 | 1 |
159 | 1 |
TOTAL | 35 |
La mayor parte de los estudiantes de ese curso tiene 155 meses. Ese dato se llama moda por que es la que mas veces se encuentra o la que tiene mayor frecuencia en el conjunto de datos.
Ahora calcularemos la media aritméticade la edad de los 35 estudiantes del curso de grado séptimo.
151 | 2 | 151 * 2 =302 |
152 | 3 | 152 * 3 = 456 |
153 | 4 | 153 * 4 = 612 |
154 | 7 | 154 * 7 = 1078 |
155 | 9 | 155 * 9 = 1395 |
156 | 6 | 156 * 6 = 936 |
157 | 2 | 157 * 2 = 314 |
158 | 1 | 158 * 1 = 158 |
159 | 1 | 159 * 1 = 159 |
Para determinar la mediana, recordemos que es el dato que ocupa la posicion de la mitad de todo el conjunto de datos que tenemos, debemos ordenar los datos de menor a mayor escribiendolos tantas veces como nos indique la frecuencia (por ejemplo, la edad de 151 meses tiene frecuencia 2 por tanto escribimos este dato 2 veces, y asì sucesivamente):
Como se trata de 35 datos, el dato central (155 meses) es el que aparece en el lugar decimo octavo lugar.
Observemos que hay 17 datos antes del 115 y también 17 después. Ese dato se llama mediana del conjunto de datos.
Ahora agrupemos los datos en intervalos de 3 meses cada uno y observemos que sucede:
TABLA B
Edad en meses | No de alumnos |
151 - 153 | 9 |
154 - 156 | 22 |
157 - 159 | 4 |
El histograma correspondiente a la característica "edad en meses" se muestra en la siguiente figura:
Podemos decir que el intervalo 154 - 156 el de mayor frecuencia. Ahora tenemos el intervalo modal o clase modal.
Podemos asegurar que el decimoctavo dato está en el intervalo 154 - 156. Este intervalo se llama intervalo medianoo clase mediana.
Edad en meses | No de alumnos | Frecuencia acumulada |
151 - 153 | 9 | 9 |
154 - 156 | 22 | 31 |
157 - 159 | 4 | 35 |
Cuando los datos se agrupan, el procedimiento para calcular la media artmética es análogo, pero se utilizan los puntos medios de cada intervalo en vez de cada uno de los datos, Veamoslo:
Intervalos de la edad en meses | |||
151 - 153 | 152 | 9 | 152 * 9 = 1368 |
154 - 156 | 155 | 22 | 155 * 22 = 3410 |
157 - 159 | 158 | 4 | 158 * 4 = 632 |
|
|
|
En este caso la media aritmética de los datos agrupados es 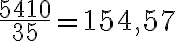 meses.
meses.
PREGUNTA: ¿En los datos agrupados, aquel que tiene la máxima frecuencia absoluta lo llamamos ________? * Clase modal * Clase mediana * Mediana * Media
Introducción a la probabilidad
La probabilidad nos permite medir la frecuencia con la que se presenta un resultado cuando se realiza un experimento.
El experimento es un procedimiento que puede tener uno o más resultados.
Por ejemplo, si lanzamos un dado al aire y deseamos determinar cuál es la probabilidad de que salga un 2, o que salga un número par, o que salga un número menor que 4.
El experimento tiene que ser aleatorio , es decir, que pueden presentarse diferentes resultados, dentro de un conjunto posible de soluciones, así se realice dicho experimento en las mismas condiciones. Esto significa que no se pueden anticipar los resultados del experimento.
Por ejemplo, si lanzamos una moneda al aire: el resultado puede ser cara o cruz, pero no sabemos de antemano cual de ellos va a salir.
O en la Lotería, el primer premio puede ser cualquier número entre el 1 y el 100.000, pero no sabemos con anticipaciòn cual puede ser.
Cada posible resultado de un experimento se llama evento o suceso. Cuando un experimento se repite varias veces es posible determinar la frecuencia con la cual se repite ese suceso y también la frecuencia relativa de cada uno, la cual corresponde a la razón entre la frecuencia absoluta y el número total de eventos.
La probabilidad mide la mayor o menor posibilidad de que se dé un determinado resultado (suceso), cuando se realiza un experimento aleatorio.
La probabilidad toma valores entre 0 y 1 (o expresados en tanto por ciento, entre 0% y 100%):
El valor cero corresponde al suceso imposible: Si lanzamos un dado al aire y la probabilidad de que salga el número 7 es cero (al menos, si es un dado certificado por la OMD, "Organización Mundial de Dados").
El valor uno corresponde al suceso seguro: Si lanzamos un dado al aire y la probabilidad de que salga cualquier número del 1 al 6 es igual a uno (100%).
El resto de sucesos tendrá probabilidades entre cero y uno: entre más alto sea el valor de la probabilidad (se acerque a 1) es más probable que el suceso se presente.
Cálculo de probabilidades:
Uno de los métodos más utilizados es aplicando la Regla de Laplace: define la probabilidad de un suceso como el cociente entre casos favorables y casos posibles.
P(A) = Casos favorables / casos posibles
Ejemplos:
a) Probabilidad de que al lanzar un dado salga el número 2:

El caso favorable es tan sólo uno (que salga el dos), mientras que los casos posibles son seis (puede salir cualquier número del uno al seis). Por lo tanto la probabilidad de que salga el dos en el dado es 1 de 6 posibles:
b) Probabilidad de que al lanzar un dado salga un número par : En este caso los casos favorables son tres (que salga el dos, el cuatro o el seis), mientras que los casos posibles siguen siendo seis. Por lo tanto:
c) Probabilidad de que al lanzar un dado salga un número menor que 5 : En este caso tenemos cuatro casos favorables (que salga el uno, el dos, el tres o el cuatro), frente a los seis casos posibles. Por lo tanto:
PREGUNTA: ¿La experiencia de tener un hijo, se puede considerar como un hecho aleatorio?
A), FALSO b) VERDADERO
Aplicación de la probabilidad en la vida cotidiana
EJEMPLO 1:
En una asignatura el profesor solicita a cada uno de sus 25 alumnos indicar cuántos hermanos o hermanas tiene.

El profesor agrupa los datos en la siguiente tabla:
Cantidad de hermanos | No de alumnos | Cantidad de hermanas | No de alumnos |
0 | 6 | 0 | 8 |
1 | 10 | 1 | 8 |
2 | 5 | 2 | 5 |
3 | 3 | 3 | 2 |
4 | 1 | 4 | 2 |
TOTAL | 25 | TOTAL | 25 |
En la tabla observamos que el total de hermanos se puede contabilizar así:

 . En total son 33 hermanos (masculino).
. En total son 33 hermanos (masculino).
El número de hermanas es se calcula:

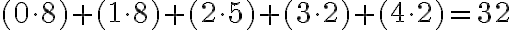 . En total son 32 hermanas (femenino).
. En total son 32 hermanas (femenino).
Sexo de los hermanos | Cantidad | Probabilidad |
Masculino (hermanos) | 33 | |
Femenino ( hermanas) | 32 |
TOTAL 65
Las experiencias de tener un hermano, tiene, respecto al sexo, dos posibles resultados, por lo cual no se puede anticipar el resultado. Por ello se considera un fenómeno aleatorio.
EJEMPLO 2:
Si una familia tiene dos hijos. ¿Cuál es la probabilidad de que ambos sean mujeres?
Nombraremos a los hombres H y a la mujeres M.
Los posibles resultados de la distribucción de sexo en una familia de dos hijos son:




HM | HH | MH | MM |
Sólo el evento MM (mujer-mujer) cumple la condición pedida.
Existen 4 sucesos posibles, pero sólo 1 cumple la condición solicitada, por tanto la probabilidad de que una familia con dos hijos ambos sean mujeres es 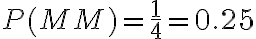 .
.
PREGUNTA: ¿Cuál es la probabilidad de obtener 5 al lanzar un dado?
A) 1/6 B) 1/5 C) 1/3 D) 1/4

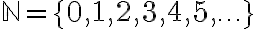
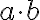



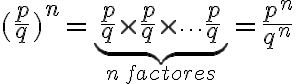




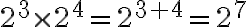






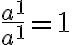








![\sqrt[n]{b}=a \sqrt[n]{b}=a](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b2480dff4dea5bb8f396c9367ebbdbac.gif)
![(\sqrt[n]{a})^m=\sqrt[n]{a^m} (\sqrt[n]{a})^m=\sqrt[n]{a^m}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e389c46f4a1d179406884b6ec47bb27a.gif)
![\sqrt[n]{a\times b\times c}=\sqrt[n]{a}\times\sqrt[n]{b}\times\sqrt[n]{c} \sqrt[n]{a\times b\times c}=\sqrt[n]{a}\times\sqrt[n]{b}\times\sqrt[n]{c}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/42449fc88ec1f27f9a3f43aa80cc0622.gif)

![\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{a}} \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{a}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b849065e0d495c38ec10214f677f53f5.gif)
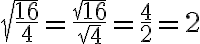

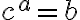












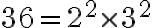










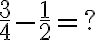




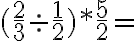
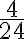
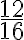
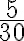
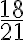
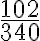
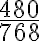
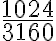
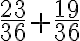
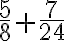
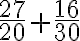
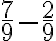
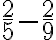
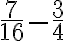
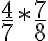
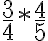
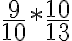
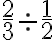
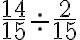
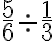
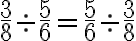
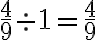
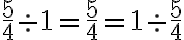
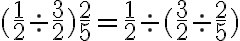




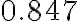

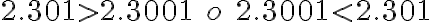


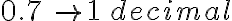
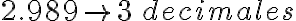



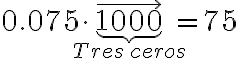



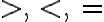

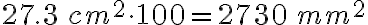


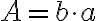


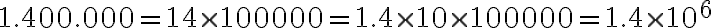

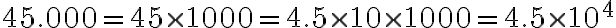
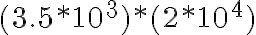
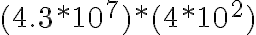
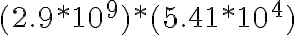
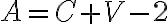
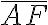
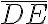
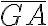
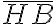
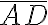
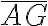
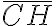
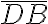
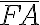
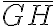
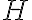
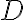


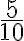

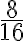
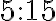







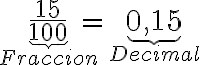


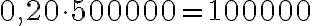


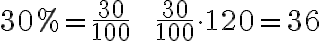






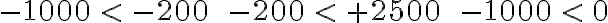






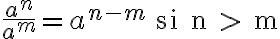


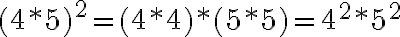

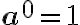
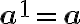

![\sqrt[5]{32} = 2, porque 2^5 = 32 \sqrt[5]{32} = 2, porque 2^5 = 32](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/1b0fc17ad4ece8bb7eeb11a38b4885a4.gif)
![\sqrt[3]{-27} = (-3), porque (-3)^3 = (-27) \sqrt[3]{-27} = (-3), porque (-3)^3 = (-27)](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/1688ede00e3e998a26ae0a82e3ef1b9f.gif)
![\Huge (\sqrt[n]{a})^m=\sqrt[n]{a^m} \Huge (\sqrt[n]{a})^m=\sqrt[n]{a^m}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/623f9e58cbef57f2b3dcbe60dc449f70.gif)
![(\sqrt[3]{27})^2=3^2=9 (\sqrt[3]{27})^2=3^2=9](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/d8f1a5c6c7096a7babc7f0293145a6f8.gif)
![\sqrt[3]{27^2}=\sqrt[3]{729}=9 \sqrt[3]{27^2}=\sqrt[3]{729}=9](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/d5bcc9eedb2749baae99a760c7ca6391.gif)
![\Huge \sqrt[n]{a*b*c}=\sqrt[n]{a}*\sqrt[n]{b}*\sqrt[n]{c} \Huge \sqrt[n]{a*b*c}=\sqrt[n]{a}*\sqrt[n]{b}*\sqrt[n]{c}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/9e6b6ad30c10869347437fa8ccee447e.gif)

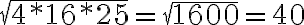
![\Huge \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}} \Huge \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/bb9a806ae9eba43129071ef402079bae.gif)

![\sqrt[3]{-125} \sqrt[3]{-125}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/fd9cd243046f8447dbca83278de1d58a.gif)
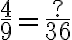







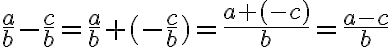




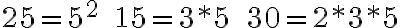










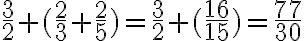
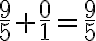
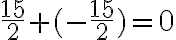




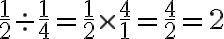



![[(\frac{4}{5})^3]^2=(\frac{4}{5})^6=\frac{4^6}{5^6} [(\frac{4}{5})^3]^2=(\frac{4}{5})^6=\frac{4^6}{5^6}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/3b2f2c30cad0821b832c11e3f3e52af3.gif)






![\sqrt[2]{\frac{100}{81}} \sqrt[2]{\frac{100}{81}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/a284ab83a5d2ffb14a718cb13733b908.gif)
![\sqrt[2]{\frac{100}{81}}=\frac{10}{9}\,\,\,\textrm{porque}\,\,\,(\frac{10}{9})^2=\frac{100}{81} \sqrt[2]{\frac{100}{81}}=\frac{10}{9}\,\,\,\textrm{porque}\,\,\,(\frac{10}{9})^2=\frac{100}{81}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/04307a9b4f25edf5e00b98eba2cf37f2.gif)
![\sqrt[5]{-\frac{1}{32}} \sqrt[5]{-\frac{1}{32}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/af11af7ad1b76ef70a1f8663b79cfd21.gif)
![\sqrt[5]{-\frac{1}{32}}=-\frac{1}{2}\,\,\textrm{porque}\,\,\,(-\frac{1}{2})^5=-\frac{1}{32} \sqrt[5]{-\frac{1}{32}}=-\frac{1}{2}\,\,\textrm{porque}\,\,\,(-\frac{1}{2})^5=-\frac{1}{32}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/919a93c6fd5246106af4270ade8e2b6f.gif)
![\sqrt[2]{\frac{25}{4}} \sqrt[2]{\frac{25}{4}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/c837fbd691cd7f10350ab83ee1fa261a.gif)
![\sqrt[2]{\frac{25}{4}}=\frac{\sqrt[2]{25}}{\sqrt[2]{4}}=\frac{5}{2} \sqrt[2]{\frac{25}{4}}=\frac{\sqrt[2]{25}}{\sqrt[2]{4}}=\frac{5}{2}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/fab7a274e2a6147d9d195399d9321e3c.gif)
![\sqrt[2]{\frac{13}{36}} \sqrt[2]{\frac{13}{36}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/7cf787d8a68a424dde44873cdd68c08e.gif)



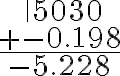





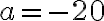



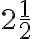






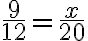

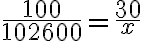











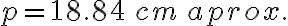



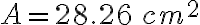


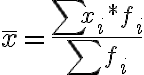
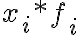




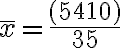




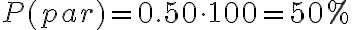


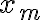



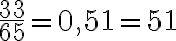
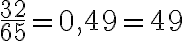




Comentarios
Publicar un comentario