Matemáticas 10º y 11º
MAURICIO MUÑOZ MATEMÁTICO FÍSICO UNIVALLE
MATEMÁTICAS 10°
VIDEO TEMA TRIGONOMETRIA
Ángulos
Los ángulos son la parte del plano comprendida entre dos semirrectas que tienen el mismo origen.
Un ángulo se dice positivo si la semirrecta OQ gira en el sentido contraria al de las manecillas del reloj.
Un ángulo se dice negativo si la semirrecta OQ gira en el sentido de las manecillas del reloj.
Así mismo , un ángulo pertenece al cuadrante en el que esta ubicado su lado terminal.
CUADRANTE 1: Comprende el eje positivo de  y el eje positivo de
y el eje positivo de  .
.
CUADRANTE 2: Comprende el eje negativo de  y el eje positivo de
y el eje positivo de  .
.
CUADRANTE 3: Comprende el eje negativo de  y el eje negativo de
y el eje negativo de  .
.
CUADRANTE 4: Comprende el eje positivo de  y el eje negativo de
y el eje negativo de  .
.
Observa:

Clases de ángulos
Ángulo recto: está formado por el cruce de dos rectas perpendiculares que forman la cuarta parte de una revolución, es decir, 90º.

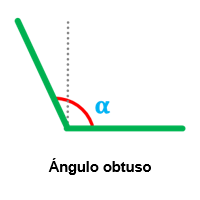
Ángulo obtuso: un ángulo obtuso tiene una abertura mayor a 90° pero menor a 180°.
Ángulo agudo: un ángulo agudo tiene una abertura mayor a 0° pero menor a 90°

Ángulo llano o plano: es aquel cuyo ángulo es de 180°

PREGUNTA: ¿Es posible medir distancias con ángulos únicamente?
Medida de ángulos
SISTEMAS DE MEDICIÓN DE ÁNGULOS
Para medir una ángulo acudimos a tres sistemas: el sistema sexagesimal, el sistema cíclico y el sistema centesimal.
Sistema sexagesimal
La circunferencia se divide en 360 partes iguales y a cada parte es lo que llamamos un grado sexagesimal.
Las unidades sexagesimales son:
Grado (1°) que equivale a 60 minutos (60´).
Minuto (1´)que equivale a 60 segundos (60´´).
Sistema cíclico
La unidad de medida es el radián.
RADIÁN: el ángulo que se consigue cuando se toma el radio y se enrolla sobre el círculo, es decir, la longitud (r) del arco formado por el ángulo de dos semirectas que también son de longitud r.
1 radián=57°18'
Ingresa a https://www.disfrutalasmatematicas.com/geometria/radianes.html para que participes en una actividad interactiva.
Se verifica entonces que:
Como la circunferencia contiene su radio  veces, resulta que un ángulo giro o de una vuelta mide
veces, resulta que un ángulo giro o de una vuelta mide  radianes.
radianes.
PREGUNTA: ¿La expresión 1° equivale a 3600´´ es correcta?
Cambio de un sistema a otro
En la practica se hace necesario expresar un ángulo dado en sistema cíclico en el sistema sexagesimal y el caso contrario.
Para cambiar de un sistema a otro se establece la siguiente proporción
La proporción permite calcular una de las medidas conocida la otra.
Ejemplo:
Expresar el ángulo 60° en radianes.
Solución:
Consideramos la proporción formada por los extremos de la fórmula anterior.
PREGUNTA: ¿A cuanto equivale el ángulo  radianes en sistema sexagesimal?
radianes en sistema sexagesimal?
Definiciones de las funciones trigonométricas.
Consideremos una circunferencia de radio r y centro el punto (0,0). La ecuación de dicha circunferencia es:
Cualquier punto (x,y) de la circunferencia satisface la ecuación  .
.
Llamaremos  al ángulo que determina la semirrecta
al ángulo que determina la semirrecta  que corta a la circunferencia en el punto P: (x,y)
que corta a la circunferencia en el punto P: (x,y)
Si tenemos un ángulo  en posición normal , en un sistema de coordenadas cartesianas, y una semirrecta
en posición normal , en un sistema de coordenadas cartesianas, y una semirrecta  que corta a la circunferencia de centro C: (0,0) en el punto P: (x,y). Definimos las funciones o razones trigonométricas con respecto al ángulo
que corta a la circunferencia de centro C: (0,0) en el punto P: (x,y). Definimos las funciones o razones trigonométricas con respecto al ángulo  así:
así:
Las tres razones trigonométricas directas del ángulo  son:
son:
Las tres razones trigonométricas inversas de las anteriores son:
Los valores de  se expresan en grados sexagesimales o en radianes principalmente.
se expresan en grados sexagesimales o en radianes principalmente.
PREGUNTA: Dado que  , ¿se cumple que
, ¿se cumple que 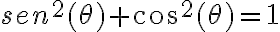 para cualquier ángulo?
para cualquier ángulo?
Funciones trigonométricas para ángulos notables
FUNCIONES TRIGONOMÉTRICAS DE ÁNGULOS NOTABLES
| Los ángulos notables son aquellos cuyas razones trigonométricas pueden ser calculados mediante consideraciones geométricas elementales. |
Los ángulos notables son: 0º, 30º, 45º, 60º, 90º, 180º, 270º y preferentemente se utilizan para ilustran ejemplos en matemáticas y física.
Analicemos los valores para las seis funciones trigonométricas de los ángulos de 0º=360º, 90º, 180º, 270º.
0º | 0 | 1 | 0 | Indeterminada | 1 | Indeterminada |
90º | 1 | 0 | Indeterminada | 0 | Indeterminada | 1 |
180º | 0 | -1 | 0 | Indeterminada | -1 | Indeterminada |
270º | -1 | 0 | Indeterminada | 0 | Indeterminada | -1 |
Los ángulos de 30º, 45º y 60º, serán estudiados en la siguiente unidad, en virtud de la aplicabilidad que tienen en la solución de triángulos isósceles, equiláteros y rectángulos.
PREGUNTA: ¿Cuánto es el valor de 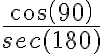 ?
?
A) INDETERMINADO B) 1 C) -1 D) 0
SIGNOS DE LOS VALORES DE LAS FUNCIONES
El signo del valor de una función trigonométrica esta determinado por el signo de las coordenadas del punto de intersección del lado final del ángulo en posición normal, con la circunferencia.
Función seno y función cosecante
Dado que el radio r es una distancia se considera siempre positivo. Así las expresiones:
Tienen el signo de la ordenada. Luego las funciones seno y cosecante son positivas en los cuadrantes I y II y son negativas en los cuadrantes III y IV.
Función coseno y función secante
Con la misma consideración del radio positivo, las expresiones
tienen el mismo signo de la abscisa. Luego las funciones coseno y secante son positivas en los cuadrantes I y IV y son negativas en los cuadrantes II y III.
Función tangente y función cotangente
Al analizar las funciones tangente y cotangente observamos que no dependen del radio y en consecuencia, dependen de los signos de la abscisa y de la ordenada.
Por tanto las funciones tangente y cotangente son positivas en los cuadrantes I y III en los cuales la abscisa y la ordenada tienen el mismo signo, y son negativas e los cuadrantes II y IV ya que la abscisa y la ordenada tienen diferente signo.
El siguiente cuadro resume las posibilidades que tienen los signo para las seis funciones trigonométricas.
CUADRANTE | SENO | COSENO | TANGENTE | COTANGENTE | SECANTE | COSECANTE |
I | + | + | + | + | + | + |
II | + | - | - | - | - | + |
III | - | - | + | + | - | - |
IV | - | + | - | - | + | - |
PREGUNTA: ¿Qué signo tendrá la función 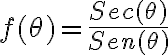 en el cuadrante IV?
en el cuadrante IV?
Determinación de las razones trigonométricas
DETERMINACIÓN
Podemos redefinir las razones trigonométricas de puntos  de una circunferencia de centro
de una circunferencia de centro  , para triángulos rectángulos, considerando que le radio corresponde a la hipotenusa.
, para triángulos rectángulos, considerando que le radio corresponde a la hipotenusa.
En el triangulo ABC, rectángulo en B y con un ángulo  que tiene como vértice a A sobre el origen, se definen las siguientes razones:
que tiene como vértice a A sobre el origen, se definen las siguientes razones:
Si llamamos ca al cateto adyacente, co al cateto opuesto y hi a las hipotenusa podemos resumir así:
Ejemplo:
Hallar las cinco razones trigonométricas que faltan sabiendo que  es un ángulo del primer cuadrantes y
es un ángulo del primer cuadrantes y  .
.
Solución:
Ahora, consideremos el triángulo rectángulo OAP:
Por el teorema de pitágoras:
Así podemos encontrar las razones trigonométricas restantes:
Luego:
PREGUNTA: Si definiésemos la función  esta correspondería a la siguiente razón:
esta correspondería a la siguiente razón:
Razones trigonométricas de los ángulos asociados a 45º
RAZONES TRIGONOMÉTRICAS
Para cada ángulo  del primer cuadrante, hay tres ángulos que llamaremos asociados a
del primer cuadrante, hay tres ángulos que llamaremos asociados a  , que tienen sus razones trigonométricas iguales en valor absoluto. Estos ángulo se determinan sobre la circunferencia y del origen.
, que tienen sus razones trigonométricas iguales en valor absoluto. Estos ángulo se determinan sobre la circunferencia y del origen.
Los ángulos asociados a 45º son 135º, 225º y 315º
para  el triangulo OPQ es rectángulo e isósceles, pues sus ángulos O y P son de 45º, luego sus catetos son iguales. Estos catetos OQ=x y PQ=x coinciden con el valor de seno y el coseno del ángulo de 45º.
el triangulo OPQ es rectángulo e isósceles, pues sus ángulos O y P son de 45º, luego sus catetos son iguales. Estos catetos OQ=x y PQ=x coinciden con el valor de seno y el coseno del ángulo de 45º.
Consideremos la circunferencia de radio 1.
Aplicando el teorema de Pitágoras a dicho ángulo triangulo se tiene:
Por tanto las razones de 45º y sus ángulos asociados son los que se indican en la siguiente tabla:
PREGUNTA: Los ángulos asociados a 45º en radianes son:
Razones trigonométricas de ángulos asociados a 60º
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS ASOCIADOS A 60º
Para  el triangulo
el triangulo  es equilátero, pues
es equilátero, pues  y el ángulo en
y el ángulo en  es de
es de  . Ademas, la altura h lo divide en dos triángulos rectángulos de hipotenusa igual a
. Ademas, la altura h lo divide en dos triángulos rectángulos de hipotenusa igual a 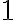 .
.
Los ángulos asociados a 60º con 120º, 240º y 300º.
Aplicando el teorema de Pitágoras al triangulo OQP, se tiene:
Luego:  y el
y el  . En la tabla siguiente encontramos los demás valores:
. En la tabla siguiente encontramos los demás valores:
EJEMPLO: Comprobar que es cierta la siguiente igualdad sustituyendo las razones que aparecen por sus valores numericos.
Solución:
Reemplacemos los valores sirviéndose de las tablas anteriores:
Razones trigonométricas de ángulos asociados a 30º
Para  el triangulo
el triangulo  tiene sus ángulos de
tiene sus ángulos de  , luego es equilátero. Al trazar su altura h se forman dos triángulos rectángulos.
, luego es equilátero. Al trazar su altura h se forman dos triángulos rectángulos.
Los ángulos asociados a  son 150º, 210º y 330º.
son 150º, 210º y 330º.
Aplicando el teorema de Pitágoras al triangulo OQP, se tiene:
Por definición resulta que sen(30º)=1/2 y cos(30º)= . En la tabla siguiente encontramos los demás valores:
. En la tabla siguiente encontramos los demás valores:
Reducción de ángulos al primer cuadrante
Para comprender el proceso de reducción de razones trigonométricas para ángulos agudos, es decir, para ángulos ubicados en el primer cuadrante comprendidos entre 0° y 90°, haremos uso del siguiente vídeo:
Fuente: https://www.youtube.com/watch?v=0alEBfZhUco
PREGUNTA: La reducción de tan 750° usando el segundo caso es:
Problemas con funciones trigonométricas
Antes de analizar las situaciones que se pueden resolver son las funciones trigonométricas, es importante reconocer la diferencia entre un ángulo de elevación y un ángulo de depresión.
El ángulo de elevación de un punto A, desde el punto O del observados, es el ángulo medido desde la horizontal que contiene a O hacia arriba, hasta la línea OB de la visual.
El ángulo de depresión de un punto A', desde el punto O del observados, es el ángulo medido desde la horizontal que contiene a O hacia arriba, hasta la línea OB' de la visual.
Ejemplo:
Desde lo alto de un faro, cuya altura sobre el nivel del mar es de 120
metros, el ángulo de depresión de una embarcación es de 15°. ¿A qué distancia del faro está la embarcación ?
Solución: Lo primero que tenemos que hacer es dibujar el triángulo que se forma con los datos del problema.
Aunque el problema viene con un ángulo de depresión de 15°, por la nota anterior el ángulo de elevación mide lo mismo. A partir de aquí hacemos uso de la relación tangente:
x = -447,93
PREGUNTA: Un niño ve un anuncio publicitario en la pared de un edificio, con un ángulo de elevación de 12º y está situado a 30m del edificio. Si del suelo a los ojos del niño hay 1,10m, ¿a qué altura se encuentra el aviso?
A) 7,5 m B) 7,48
m C) 6 m D) 8 m
SITIO WEB FUNCIONES TRIGONOMETRICAS
https://www.zweigmedia.com/MundoReal/trig/trig2.html
Variación de las funciones trigonométricas
Antes de continuar con el análisis de estas funciones, es necesario hacer algunas precisiones en el lenguaje a usar:
Si 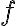 es una función definida en un subconjunto
es una función definida en un subconjunto  de
de  y además
y además  y
y  son elementos cualesquiera de
son elementos cualesquiera de  entonces:
entonces:
 (infinito), los valores numéricamente tan grandes como se quiere para abreviar hechos como el caso de
(infinito), los valores numéricamente tan grandes como se quiere para abreviar hechos como el caso de  si
si  se aproxima a
se aproxima a  por su izquierda se tiene que
por su izquierda se tiene que  y si
y si  se acerca a
se acerca a  por su derecha se tiene que
por su derecha se tiene que  .
.La función y = sen x
Se considera la función  , donde
, donde  es el valor de un ángulo medido en radianes, por lo que
es el valor de un ángulo medido en radianes, por lo que  , puede ser cualquier número real y
, puede ser cualquier número real y  es el valor del seno del ángulo
es el valor del seno del ángulo  .
.
Cuando el ángulo es mayor que 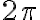 o menor que cero, el valor de
o menor que cero, el valor de  se puede reducir según ya estudiamos, a un valor correspondiente de
se puede reducir según ya estudiamos, a un valor correspondiente de  , pero comprendido entre 0 y
, pero comprendido entre 0 y 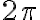 radianes. Así, la gráfica de
radianes. Así, la gráfica de  tendrá la siguiente forma:
tendrá la siguiente forma:
... | 0 | ... | |||||||||||||||||
... | 0 | 1 | 0 | -1 | 0 | ... |
Del análisis de la gráfica se deducen las siguientes propiedades:
PREGUNTA: El periodo de la función  es
es
La función y = cos x
De forma análoga a como se ha analizado el comportamiento de la función seno, se realiza el estudio de la función coseno, en el caso de  y se amplía después para todo
y se amplía después para todo  . La gráfica que se muestra a continuación se obtiene de la siguiente tabla de valores conocidos:
. La gráfica que se muestra a continuación se obtiene de la siguiente tabla de valores conocidos:
... | 0 | ... | |||||||||||||||||
... | 1 | 0 | -1 | 0 | 1 | ... |
Del análisis de la gráfica se deducen las siguientes propiedades:
PREGUNTA: La función  es impar.
es impar.
La función y = tan x
Para dibujar la gráfica de la función  , recurrimos a una tabla de valores de
, recurrimos a una tabla de valores de  en el caso:
en el caso:
... | 0 | ... | |||||||||||||||||
... | No existe | -1 | 0 | 1 | No existe | -1 | 0 | 1 | No existe | -1 | 0 | ... |
Del análisis de la gráfica se deducen las siguientes propiedades:
La función y = ctg x
Bajo las mismas consideraciones que hemos desarrollado para las funciones anteriores, procederemos para las funciones recíprocas. En estos casos, las gráficas se acompañan de líneas discontinuas que representan las funciones recíprocas.
... | 0 |
|
|
| |||||||||||||||
... | 0 | -1 | No existe | 1 | 0 | -1 | No existe | 1 | 0 | -1 | 0 |
|
|
|
|
Del análisis de la gráfica se deducen las siguientes propiedades:
PREGUNTA: ¿La función cotangente es?
MAURICIO MUÑOZ MATEMÁTICO FÍSICO UNIVALLE
MATEMÁTICAS 11°
NÚMEROS REALES
El conjunto de los números reales se denota con la letra R.
Está conformado por todos los conjuntos numéricos vistos anteriormente. Veamos el diagrama:
Observemos ahora los conjuntos que conforman a los números reales

La recta proporciona una visualización perfecta de los números reales. Cada punto de la recta corresponde a uno y solo un numero real, y
viceversa.
Observa en la recta los puntos de coordenadas enteras.
Ahora observa la recta con puntos de coordenadas y puntos de coordenadas racionales:
Finalmente ubicamos los irracionales, que no pueden representarse como decimales finitos o periódicos, sino mediante una aproximación decimal:
Ahora ya podemos realizar operaciones de cualquier índole combinando operaciones de los conjuntos que conforman los números reales.
En el vídeo se observan la clasificación de los números Reales:
PREGUNTA: Las operaciones con radicales hacen parte de las operaciones entre números reales. ¿Por qué?
INTERVALOS EN LA RECTA NUMÉRICA
Se llama intervalo al conjunto de números reales, se denotan  comprendidos entre dos puntos de la recta: a y
comprendidos entre dos puntos de la recta: a y  que se llaman extremos del intervalo.
que se llaman extremos del intervalo.
En la recta real se definen los siguientes conjuntos :
Intervalo abierto de extremos a y b
Esta representación, se llama por extensión y se lee: x que pertenece a los números reales, tales que "a" es menor que x y "x" es menor que "b":
El círculo en cada valor queda vacío para indicar en la recta, que los valores no se incluyen en el intervalo:
Intervalo cerrado de extremos a y b
Esta representación, se llama por extensión y se lee: x que pertenece a los números reales, tales que "a" es menor o igual que x y "x" es menor o igual que "b":![[a,b]=\{x \epsilon \mathbb{R}| a \leq x \leq b\} [a,b]=\{x \epsilon \mathbb{R}| a \leq x \leq b\}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/ba115a11b4e38273b67e71c2ccab1e13.gif)
El círculo en cada valor sí se rellenan para indicar en la recta, que los valores se incluyen en el intervalo:
Intervalo semi abierto por la derecha.
Esta representación, se llama por extensión y se lee: x que pertenece a los números reales, tales que "a" es menor o igual que x y "x" es menor que "b":
Intervalo semi abierto por la izquierda.
Esta representación, se llama por extensión y se lee: x que pertenece a los números reales, tales que "a" es menor que x y "x" es menor o igual que "b".![(a,b]=\{x \epsilon \mathbb{R}| a < x \leq b\} (a,b]=\{x \epsilon \mathbb{R}| a < x \leq b\}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/0bb20e270421a3b08958e0e10c713882.gif)
Intervalo infinito abierto por la izquierda.
Se deja una flecha indicando que será "infinito" en el intervalo porque nunca se termina:
Intervalo infinito cerrado por la izquierda.
Intervalo infinito abierto por la derecha.
Intervalo infinito cerrado por la derecha.
En esta lección es importante que aprendas a diferenciar la simbología de los intervalos abiertos "()", cerrados "[ ]", semi abierto e infinitos "[ ) y ( ]".
PREGUNTA: ¿Cual de los siguientes intervalos es semi abierto por la izquierda?
a) (3 , 67] b) (-3 , -1) c) [-4 , 8) d) (-¥
, 5)
DESIGUALDADES O INECUACIONES
Una inecuación es una desigualdad en la cual intervienen expresiones algebraicas. Estas se refieren a relaciones de orden definidas en los números reales del tipo 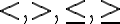
Propiedades de las desigualdades:
Propiedades para realizar operaciones con desigualdades:
1. Si se suma o se resta una misma cantidad en los dos miembros de la desigualdad, la relación se mantiene, es decir, el símbolo de desigualdad no se afecta.
| 2<9 | 2<9 |
| 2+3<9+3 | 2-3<9-3 |
| 5<12 | -1<6 |
2. Si se multiplica o divide por una cantidad positiva en ambos miembros de la desigualdad, la relación se mantiene.
| 2<9 | 2<9 |
 | |
| 8<36 |
3. Si se multiplica o se divide por una cantidad negativa en ambos miembros de la desigualdad, la relación cambia de sentido, es decir, se invierte el símbolo de la desigualdad.
| $<9 | 2<9 |
 | |
| -10>-45 | 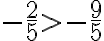 |
Ejemplo:
Hallar el conjunto solución de la desigualdad: 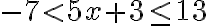
1. Como debemos despejar x de la inecuación, primero se debe restar 3 en todos los miembros de la desigualdad:
2. Ahora dividimos en 5 todos los miembros de la inecuación:
Luego: el conjunto solución es (-2,2] y la gráfica correspondiente es:
En los siguientes vídeos podrá profundizar mejor el tema:
PREGUNTA: El conjunto de valores que satisfacen la desigualdad 2x-5<9 es:
a) x ≤ 6 b) x<7 c) x ≥ 6
d) x≤ 7
ECUACIONES E INECUACIONES CON VALOR ABSOLUTO
Cualquier número 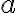 tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto
tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto 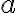 al origen (0), sobre la recta.
al origen (0), sobre la recta.
El valor absoluto de un numero real 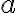 , que se denota |a|, se define como el mismo numero a si
, que se denota |a|, se define como el mismo numero a si  y el opuesto de
y el opuesto de 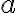 si a<0. Es decir:
si a<0. Es decir:
Esto significa que el valor absoluto de cualquier valor numérico SIEMPRE es positivo.
Ejemplo:
Propiedades del valor absoluto:
Ejemplo:
Ejemplo:
Ejemplo:
Ejemplo:
5. |a|=|-a|
Ejemplo:
|9|=|-9|=9
Ejemplo:
Ejemplo:
R=[3,7]
Ejemplo:
Veamos otros ejemplos:
1. Calculemos: 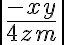 si x > 0; y < 0; z < 0; m > 0
si x > 0; y < 0; z < 0; m > 0
Solución:
Solución: Por la propiedad número 7, tenemos:
Solución:
En el siguiente vídeo se muestran varios ejercicios resueltos que le ayudarán a profundizar el tema:
PREGUNTA: Cuál es el resultado de $x+4|<2
a) R=(-6,-2) b) R=[-6,-2]
c) R=(6,-2) d) R=(-6,2)
FUNCIONES
Una función es el término
Una relación es función si:
* Todo elemento del conjunto de partida A debe tener imagen.
* La imagen de cada elemento x  A debe ser única. Es decir, ningún elemento del dominio puede tener más de una imagen, pero cada imagen puede tener varios dominios.
A debe ser única. Es decir, ningún elemento del dominio puede tener más de una imagen, pero cada imagen puede tener varios dominios.
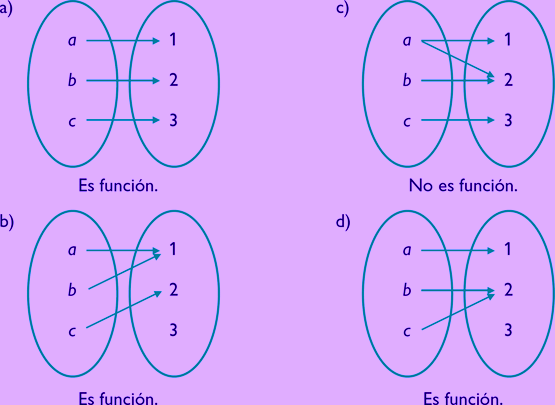
En una función real hay dos tipos de variables:
- La letra x representa cualquier numero real y se llama variable independiente. Al conjunto de estas variable se le denomina el dominio de la función.
- Los valores que toma la letra y dependen de los valores que se dan a la letra x, por eso la variable y se llama variable dependiente. Al conjunto de los valores de esta variable se le denomina rango.
El subconjunto en el que se define la función se llama dominio o campo existencia de la función. Se designa por D.
Se denomina recorrido de una función al conjunto de los valores reales que toma la variable y o f(x).
Ejemplo:
Veamos el dominio y el recorrido de la función 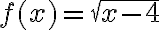 .
.
La función f(x) no esta definida sobre toda la recta real puesto que x-4 debe ser positivo. Por tanto  , es decir
, es decir  .
.
La función 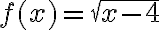 nunca será negativa. Por lo tanto
nunca será negativa. Por lo tanto 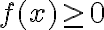 .
.
OPERACIONES CON FUNCIONES
Adición de funciones
Sean f y g dos funciones reales de variable real definidas en un mismo intervalo. Se llama suma de ambas funciones, y se representa por f + g, a la función definida por
(f + g)(x) = f(x) + g(x)
Ejemplo 1: Sean las funciones f(x) = 3 x + 1, y g(x) = 2 x - 4. Definir la función f + g.
Solución
- La función f + g se define como
(f + g)(x) = f(x) + g(x)
3x + 1 + 2 x - 4
5 x - 3
Resta de funciones
Del mismo modo que se ha definido la suma de funciones, se define la resta de dos funciones reales de variable real f y g, como la función
(f - g)(x) = f(x) - g(x)
Para que esto sea posible es necesario que f y g estén definidas en un mismo intervalo.
Ejemplo 2: Sean las funciones f(x) = 3 x + 1, y g(x) = 2 x - 4. Definir la función f - g.
Solución
- La función f - g se define como
(f - g)(x) = f(x) - g(x)
3x + 1 - (2 x - 4)
3x + 1 - 2x + 4
x + 5
Producto de funciones
Sean f y g dos funciones reales de variable real, y definidas en un mismo intervalo. Se llama función producto de f y g a la función definida por
(f.g)(x) = f(x).g(x)
Ejemplo 3: Sean las funciones f(x) = 3 x + 1, y g(x) = 2 x - 4. Definir la función f . g.
Solución
- La función f . g se define como
(f .g)(x) = f(x) . g(x)
(3x + 1) . (2x - 4)
3x.2x +3x.(-4) + 1.2x +1.(-4)
Cociente de funciones
Dadas dos funciones reales de variable real, f y g, y definidas en un mismo intervalo, se llama función cociente de f y g a la función definida por
(f/g)(x) = f(x)/g(x)
(La función f/g está definida en todos los puntos en los que la función g no se anula)
Ejemplo 4: Sean las funciones f(x) = 3 x + 1, y g(x) = 2 x - 4. Definir la función f / g.
Solución
- La función f / g se define como
(f /g)(x) = f(x) / g(x)
(3x + 1) / (2x - 4)
Producto de un número por una función
Dado un número real a y una función f, el producto del número por la función es la función definida por
(a.f)(x) = a.f(x)
Ejemplo 5: Sea la función f(x) = 3 x + 1 y el número real a=7 Definir la función a.f .
Solución
- La función a . f se define como
(a.f)(x) = a.f(x)
7.(3x + 1)
7.3x +7.1
21x + 7
PREGUNTA: Sean las funciones (x)=2x+3 y g(x)=5x+8. Cuál es el resultado de la operación (f.g)(x)
a) 10x2+31x+24 b) 10x2+30x+24 c) 10x2+x+24 d) 10x2-x+24
FUNCIONES COMPUESTAS
Si f y g son dos funciones y el dominio de g esta contenido en el rango de f, entonces la función compuesta de f y g se define como ![f\circ g=f[g(x)] f\circ g=f[g(x)]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/ef9b267cbe588453b7769423307444fb.gif) , donde el dominio de
, donde el dominio de  es el subconjunto del dominio de f que contiene los valores para los que
es el subconjunto del dominio de f que contiene los valores para los que  está definida.
está definida.
PROCEDIMIENTO PARA HALLAR FUNCIÓN COMPUESTA
![\Large f\circ g=f[g(x)] \Large f\circ g=f[g(x)]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/dd4bc1d78d0633cda83faa7286abcb23.gif) se lee f compuesta g y para hallar la función compuesta
se lee f compuesta g y para hallar la función compuesta  debemos:
debemos:
1. Tomar la función f y reemplazar, en cada posición donde esté x, por g(x).
Recordemos que el orden de la expresión nos indica cuál es la función que estará compuesta por la otra, así 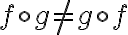
Ejercicio práctico 1:
Hallar la función compuesta  si
si  y
y  .
.
Tomamos la función f y reemplazamos, en cada posición donde esté x, por g(x).
Ejercicio práctico 2:
Hallar la función compuesta  si
si  y
y  .
.
Tomamos f(x) y lo reemplazamos en g
Por tanto:
Ejercicio práctico 3:
Un grupo de obreros está construyendo una plaza en forma circular, la cual debe tener 40 metros de diámetro. Los ingenieros calcularon la relación entre el radio de la circunferencia y el tiempo que invierten en el trabajo por medio de la fórmula r=2t+4
¿calcular el tiempo que tárdara la firma constructora en terminar la obra?
Solución:
Sabemos que el área de una circunferencia se expresa en función del radio así:
pero el radio a su vez está dado en función del tiempo:
r(t)=2t+4
Ahora vamos a expresar el área de la plaza en términos del tiempo así:
Hemos hallado el área de dicha circunferencia en función del tiempo. Como el radio es de 20 m, se tiene:
20=2t+4
entonces t=8 unidades de tiempo
Luego: la firma constructora terminará la obra en 8 unidades de tiempo.
Observa que le área se halla aplicando dos funciones sucesivamente, r y después A, y se dice que la función A(r(t)) es la compuesta de A respecto de r y se nota así:
PREGUNTA: Hallar 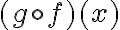 de las funciones
de las funciones  y
y 
Función inversa o reciproca
FUNCIÓN INVERSA
Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a) = b, entonces f−1(b) = a.
Es necesario que no se vaya a confundir entre la función inversa, f−1(x), y la inversa de una función,  , son totalmente diferentes.
, son totalmente diferentes.
PROCEDIMIENTO PARA CALCULAR LA FUNCIÓN INVERSA
1. Se escribe la ecuación de la función con x e y, si aparece el término f(x) lo remplazamos por y (f(x)=y).
2. Se despeja la variable x. Cuando ya esté despejada se cambia x por 
3. Se intercambian las variables, es decir, la variable y se cambia por x
Ejemplo:
Calcular la función inversa  de la función
de la función  .
.
1. Se escribe la ecuación de la función con x e y, si aparece el término f(x) lo remplazamos por y (f(x)=y).
2. Se despeja la variable x. Cuando ya esté despejada se cambia x por 
y(x+5)=3x+2
yx+5y=3x+2
yx-3x=-5y+2
x(y-3)=-5y+2

PREGUNTA: Calcular la función inversa de f(x)=3x-5:
a) f-1(x)=x+3/5 b) f-1(x)=3/x+5 c) f-1(x)=x+5/3 d) f-1(x)=5/x+3
SUCESIONES NUMÉRICAS
Una sucesión es una función definida para el conjunto de los enteros positivos.
Recorrido de una sucesión: Subconjunto ordenado de números reales, que se denota:
(a_n)=(a_1,a_2,a_3,...,a_n) para 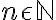
Término de una sucesión: En la sucesión (a_n)=(a_1,a_2,a_3,...,a_n) cada 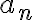 , es un término y el subíndice n indica el lugar que el término ocupa en la sucesión. Entonces:
, es un término y el subíndice n indica el lugar que el término ocupa en la sucesión. Entonces:
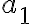 es el primer término de la sucesión.
es el primer término de la sucesión.
 es el segundo término de la sucesión.
es el segundo término de la sucesión.
 es el tercer término de la sucesión, etc.
es el tercer término de la sucesión, etc.
Una sucesión es ordenada ya que hay un primer término a1 que es imagen de 1, un término a2 que es imagen del 2 y así sucesivamente.
Para todo entero positivo n, existe un término 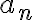 llamado término general o término n-ésimo que determina los elementos de la sucesión: podemos decir que es la fórmula por medio de la cual se halla cada uno de los términos de la sucesión.
llamado término general o término n-ésimo que determina los elementos de la sucesión: podemos decir que es la fórmula por medio de la cual se halla cada uno de los términos de la sucesión.
Ejemplo:
Escribir el término general 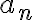 de la sucesión de los números impares.
de la sucesión de los números impares.
Solución:
La sucesión (an) de los números impares es (an) = (1,3,5,7,9,11,13...)
Por tanto el término general de los números impares es  .
.
Hallemos los tres primeros términos de  para comprobarlo:
para comprobarlo:
Para n=1 | Para n=2 | Para n=3 |
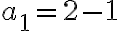 | 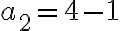 |  |
Veamos otro ejemplo:
Encontrar el término n-ésimo (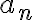 )de la sucesión
)de la sucesión 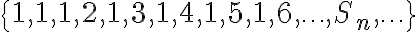
Solución:
Si observamos los términos que ocupan lugares impares, tenemos:
Si observamos los términos que ocupan lugares pares, tenemos:
Representación de sucesiones en el plano cartesiano
Representaremos en el plano cartesiano la sucesión 
La gráfica cartesiana de la sucesión  representa el conjunto de parejas ordenadas
representa el conjunto de parejas ordenadas 
La gráfica cartesiana de una sucesión no es una linea continua, sino que es un conjunto de puntos.
PREGUNTA: Encontrar los primeros cuatro términos de la sucesión 
* (d_n)=(7,9,11,13...) * (d_n)=(6,8,10,12,...) * (d_n)=(1,3,5,7,...)$ * (d_n)=(5,7,9,11,...)
SUCESIONES FINITAS E INFINITAS
Sucesión finita: Se presenta cuando el dominio de la función es un subconjunto finito de  . Esto significa que se limita el número de términos que se deben hallar a una cantidad finita.
. Esto significa que se limita el número de términos que se deben hallar a una cantidad finita.
Para encontrar los términos de una sucesión finita, hallamos los términos de la sucesión hasta el número n que se indique.
Ejemplo:
Encontrar los 5 primeros términos de la siguiente sucesión finita:
Solución:
Reemplazamos para n = 1,2,3,4 y 5.
Luego:
Sucesión infinita: Se presenta cuando el dominio de la función es el conjunto de los números enteros positivos, es decir cuando el dominio es infinito. En este caso los términos a hallar no se limitan a unos cuantos si no a todo el conjunto de números enteros positivos hasta el infinito.
Como es dispendioso encontrar todos los términos de una sucesión infinita, hallamos en orden algunos de los primeros términos e indicamos con puntos suspensivos que la sucesión continua.
Ejemplo:
Hallar los términos de la sucesión 
Solución: Observemos que en las sucesiones finitas se indica la cantidad de términos que se deben hallar, en este caso no se indica, lo que significa que es una sucesión infinita.
PREGUNTA: Los términos n=1,2 y 3 de la sucesión 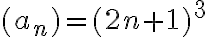 son:
son:
a) a1=8 a2=27 a3=343 b) a1=8 a2=27 a3=643 c) a1=27 a2=64 a3=343 d) a1=27 a2=125 a3=343
SUCESIONES MONÓTONAS
Una sucesión es monótona cuando todos sus términos sucesivos (a_n)=(a_1,a_2,a_3,...,a_n,...) crecen o decrecen.
Sucesión monótona creciente: Si cada término de la sucesión es mayor o igual al término anterior. Es decir,
Sucesión estrictamente creciente:Si la relación que hay entre cada término es:
Sucesión monótona decreciente: Si cada término es menor o igual al término anterior. Es decir:
Sucesión estrictamente decreciente: Si la relación que hay entre cada término y el siguiente es:
Ejemplo:
La sucesión  es monótona decreciente porque:
es monótona decreciente porque:
 (al disminuir el denominador, el valor de la fracción aumenta).
(al disminuir el denominador, el valor de la fracción aumenta).
Compruébalo remplazando algunos valores de n.
La sucesión  es monótona creciente ya que
es monótona creciente ya que 
Compruébalo remplazando algunos valores de n.
Sugerencia: Reemplaza algunos valores de la sucesión y verifica numéricamente la relación entre ellos.
SUCESIONES ACOTADAS
Una sucesión puede tener cota superior o inferior.
Sucesión acotada superiormente: Una sucesión (an) esta acotada superiormente si todos los términos de la sucesión son menores o iguales que k, es decir 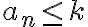 para todo n.
para todo n.
Sucesión acotada inferiormente: Una sucesión (an) esta acotada inferiormente si todos los términos de la sucesión son mayores o iguales a  , es decir
, es decir  para todo
para todo  .
.
Ejemplo:
Remplazamos unos cuantos valores para obtener los primeros términos de la sucesión:
Podemos observar que a medida que se remplazan valores más grandes de  los términos de la sucesión se van haciendo más pequeños que 1. Esto significa que está acotada superiormente por k=1.
los términos de la sucesión se van haciendo más pequeños que 1. Esto significa que está acotada superiormente por k=1.
Veamos otro ejemplo:
La sucesión  no es acotada ni superior ni inferiormente.
no es acotada ni superior ni inferiormente.
SUCESIONES CONVERGENTES, DIVERGENTES Y OSCILANTES
En la lección anterior vimos como las sucesiones pueden ser acotadas superior e inferiormente.
Ahora estudiaremos cómo se clasifican éstas sucesiones acotadas:
Sucesiones convergentes
Una sucesión (a_n)=(a_1,a_2,a_3,...,a_n,...) es convergente si todos los términos (a_n) de la sucesión se van aproximando cada vez mas a un cierto numero real al que se llama punto de convergencia o limite.
Ejemplo:
Encontrar el punto de convergencia de la sucesión 
Solución:
Se observa que todos sus términos son menores que 2 pero si remplazamos valores cada vez más grandes de "n" todos sus términos se van acercando a 1. Luego el punto de convergencia o límite de esta sucesión es 1.
Sucesiones Divergentes: Una sucesión (a_n)=(a_1,a_2,a_3,...,a_n,...) es divergente si todos los términos (a_n) de la sucesión no se aproximan a un valor real.
Por tanto las sucesiones divergentes no tienen límite.
Ejemplo:
Verificar que la sucesión (a_n)=(n+3 es divergente.
Solución:
Los primeros términos de la sucesión  nos muestran que la sucesión no se acerca a ningún valor real, por el contrario sus términos son cada vez más grandes, es decir, tienden a
nos muestran que la sucesión no se acerca a ningún valor real, por el contrario sus términos son cada vez más grandes, es decir, tienden a  .
.
Por tanto la sucesión(a_n)=(n+3) es divergente.
Veamos otro ejemplo:
La secuencia 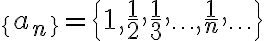 es convergente porque:
es convergente porque:
La secuencia 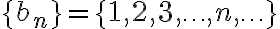 es divergente porque:
es divergente porque:
porque cuando n se hace muy grande, 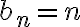 se hace muy grande y no se aproxima a ningún valor constante, por el contrario tiende a
se hace muy grande y no se aproxima a ningún valor constante, por el contrario tiende a  .
.
Sucesiones oscilantes: Una sucesión (a_n)=(a_1,a_2,a_3,...,a_n,...) es oscilante cuando sus términos no convergen ni divergen a ningún valor. esto significa que los término de la sucesión alternand de mayor a menor o visceversa.
Ejemplo:
Observamos que el primer término es mayor al segundo, el segundo es menor que el tercero, el tercer término es mayor que el cuarto término y así sucesivamente.
DEFINICIÓN DE LÍMITE
El concepto de límite en matemáticas tiene el sentido de “lugar” hacia el que se dirige una función en un determinado punto o en el infinito. Dada una función f(x) y un punto x=a se dice que el límite de f(x) cuando x se acerca a a es L, y se expresa como:
Dado 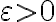 , existe
, existe  tal que siempre que |x − a| < δ, entonces |f(x) − L| <
tal que siempre que |x − a| < δ, entonces |f(x) − L| < 
Lo que viene a expresar esta formulación matemática es que si  está suficientemente cerca de a, entonces su imagen f(x) también está muy próxima a L.
está suficientemente cerca de a, entonces su imagen f(x) también está muy próxima a L.
PROPIEDADES DE LÍMITES:
Dentro de las propiedades de límites tenemos:
1 Límite de una constante.
2 Límite de una suma.
3 Límite de un producto.
4 Límite de un cociente.
5 Límite de una potencia.
6 Límite de una función.
7 Límite de una raíz.
PREGUNTA:  a) 4 b) 2 c) -1 d) 1
a) 4 b) 2 c) -1 d) 1
LIMITES LATERALES
Límite por la derecha:Se define el límite lateral por la derecha de a de la función f(x), y se expresa como:
al límite al que se acerca f(x) cuando x se acerca a a y toma valores mayores que a.
Límite por la izquierda: Se define el límite lateral por la izquierda de 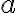 de la función f(x), y se expresa como:
de la función f(x), y se expresa como:
y se define como el límite al que se acerca f(x) cuando x se acerca a a y toma valores menores que a.
Para que una función f(x) tenga límite en x=a es necesario y suficiente que existan ambos límites laterales y coincidan, es decir:
Ejemplo:
Considera la función  . Calcular el limite cuando
. Calcular el limite cuando  por la derecha y cuando
por la derecha y cuando  por la izquierda.
por la izquierda.
Solución:
Límite por la derecha: Cuando  , podemos efectuar la tabla:
, podemos efectuar la tabla:
Límite por la izquierda: Cuando  , podemos efectuar la tabla:
, podemos efectuar la tabla:
Luego: los valores obtenidos para f( x) por la derecha y por la izquierda son diferentes. Significa que el límite de la función no existe.
Recordemos que una función sólo puede tener límite.
Una vez definido los limites laterales, podemos afirmar que si una función es continua en [a, b], decimos que f es continua por la derecha en a y continua por la izquierda en b.
PREGUNTA: ¿Qué valores se deben tomar para elaborar la tabla de valores que permita calcular el límite de una función f(x) por la derecha  ?
?
TIPOS DE LIMITES
Límites infinitos en un punto finito:
Observando la gráfica, se dice que el límite cuando x se acerca por la derecha de a es  , pues a medida que la x se acerca a a la función se hace cada vez mayor (
, pues a medida que la x se acerca a a la función se hace cada vez mayor (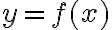 ) tiende a
) tiende a  ):
):
De igual modo se define el límite −∞ cuando nos acercamos a a sea por la derecha o por la izquierda (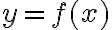 ) tiende a −∞ .
) tiende a −∞ .
Límites finitos en el infinito: Se dice que una función tiene límite b cuando x tiende a +∞ cuando la función se acerca a b cuando la x se hace cada vez mayor, es decir:
En este caso el límite es 2 cuando x tiende a + ∞ .
De igual modo se define el límite finito cuando x tiende a −∞ .
Límites infinitos en el infinito: Aparece este caso cuando si x tiende a + ∞ la función se hace cada vez mayor o menor (lo mismo si x tiende a −∞ ).
Vea en el vídeo siguiente las propiedades de los límites:
PREGUNTA: Si se tiene una función en la cual a medida que x se acerca a un punto f(x) tiende a infinito se dice que es un límite:
CALCULO DE LÍMITES EN EL INFINITO
En esta lección nos enfocaremos en aprender a calcular límites cuando tienden a  o
o 
Límites de polinomios : El límite de cualquier polinomio cuando x tiende a ∞ siempre es +∞ o −∞, dependiendo del coeficiente del término de mayor grado del polinomio.
Ejemplos:
Como podemos ver el término de mayor grado es  como su coeficiente es positivo el límite será
como su coeficiente es positivo el límite será 
En este caso, el término de mayor grado es  como su coeficiente es negativo el límite será
como su coeficiente es negativo el límite será 
Caso 1: Indeterminación  : Si tenemos un cociente (división) de polinomios nos encontraremos con una indeterminación de este tipo. Para resolverla basta recordar las siguientes reglas:
: Si tenemos un cociente (división) de polinomios nos encontraremos con una indeterminación de este tipo. Para resolverla basta recordar las siguientes reglas:
a)  si el grado de p(x)>q(x), donde el signo depende de los coeficientes (se debe aplicar ley de signos).
si el grado de p(x)>q(x), donde el signo depende de los coeficientes (se debe aplicar ley de signos).
Ejemplo:
Porque el grado del numerador es mayor, pero los respectivos coeficientes de mayor grado tienen signo diferente.
Ejemplo:
Porque el grado del denominador es mayor.
Ejemplo:
Porque el grado del numerador es igual al grado del denominador.
La resolución de límites cuando  tiende a − ∞ se reduce a las tres reglas anteriores ya que:
tiende a − ∞ se reduce a las tres reglas anteriores ya que:
Ejemplo:
Porque el grado del numerador es mayor que el grado del denominador.
d) Cociente de polinomios cuando aparecen raíces cuadradas.
Puesto que el grado del denominador es 2 y en el numerador la mayor potencia de x está dentro de una raíz cuadrada y es 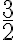 que es menor que 2.
que es menor que 2.
e) Cociente de polinomios cuando aparecen raíces cuadradas y el límite no existe
Ejemplo:
A pesar de que los grados de numerador y denominador son iguales, cuando x tiende a + ∞ (es positivo y muy grande) resulta que -x+1 es negativo y como es bien conocido, la raíz cuadrada de un número negativo no existe en el cuerpo de los números reales, por tanto el límite anterior no tiene sentido.
f) Cociente de polinomios cuando aparecen raíces cuadradas y el límite tiende a 
Ejemplo:
Caso 2: Indeterminación  : Cuando aparece esta indeterminación, si tenemos una resta de fracciones, simplemente se hace la resta para obtener un cociente de polinomios que ya sabemos aprendimos a resolver.
: Cuando aparece esta indeterminación, si tenemos una resta de fracciones, simplemente se hace la resta para obtener un cociente de polinomios que ya sabemos aprendimos a resolver.
Ejemplo:
Primero hallamos el común denominador:
Ahora realizamos la multiplicación respectiva tanto en numerador como en denominador:
Porque el grado del numerador es igual al grado del denominador.
En caso de que aparezca una raíz, el proceso es multiplicar y dividir por el conjugado de la expresión radical.
Ejemplo:
Multiplicamos y dividimos por el conjugado del radical:
Efectuamos las operaciones pertinentes:
Porque el grado del numerador es mayor al grado del denominador.
Ver el siguiente vídeo para profundizar:
a) 2 b) 7/3 c) 1 d) 4
CÁLCULO DE LIMITES EN PUNTOS FINITOS
En esta lección nos enfocaremos en aprender a calcular límites cuando tienden a valores reales finitos.
Si queremos calcular el límite de una función f(x) cuando x se acerca a cierto valor a, simplemente se debe sustituir el valor de a en f(x):
Ejemplo:
El problema que podemos encontrar en este caso es que el denominador se haga 0 al sustituir x p or el valor que corresponda.
Es por eso que veremos los casos que podemos encontrar y la forma de solucionarlos.
Caso 1: Indeterminación  con
con  : Se presenta cuando en el numerador aparece un número cualquiera diferente de 0 y el denominador es 0.
: Se presenta cuando en el numerador aparece un número cualquiera diferente de 0 y el denominador es 0.
En este caso el límite el siempre ∞ , pero para determinar su signo, se calculan los límites laterales.
Recordemos que para calcular límites laterales se deben tomar valores muy pequeños cercanos a límite que nos indiquen tanto por la derecha como por la izquierda y remplazarlos en la función.
Ejemplo:
Veamos la tendencia del límite por la derecha y por la izquierda:
Para realizar el cálculo del límite por la derecha tomemos el valor 1.0001 que es muy cercano al límite que nos indican: 1
El numerador tiende a -1 y el denominador a 0 por la izquierda, se puede interpretar como -0, aplicamos ley de signos:
Ahora para realizar el cálculo del límite por la izquierda tomemos el valor 0.9999 que es muy cercano al límite que nos indican: 1
El numerador tiende a -1 y el denominador a 0 por la derecha, se puede interpretar como +0, aplicamos ley de signos:
Indeterminación  : En este caso tanto numerador como denominador se hacen 0.
: En este caso tanto numerador como denominador se hacen 0.
Si en el numerador y en el denominador tenemos polinomios, la forma de resolver la indeterminación es descomponer los polinomios en factores y simplificar para posteriormente volver a sustituir.
Veamos un ejemplo:
En caso de que también aparezcan raíces cuadradas, realizamos el proceso explicado en la lección anterior de multiplicación por la conjugada del radical.
a) 1/8 b) 0 c) 8 d) -8
CÁLCULO DE LÍMITES EXPONENCIALES
Recordemos unas reglas básicas cuando aparecen exponentes.
Donde:
a es la base
b es el exponente
c es la potencia
Si tenemos funciones como las siguientes:
Se pueden presentar los casos que veremos a continuación.
1. La base tiende a un número cualquiera diferente de cero y el exponente a otro número que pertenezca a los reales. En este caso el límite es el número que resulta de realizar la operación correspondiente.
Ejemplo:
2. La base tiende a un número positivo mayor que 1 y el exponente a +∞ . En este caso el límite es también + ∞ .
Ejemplo:
Como vemos numerador y denominador tienen grados iguales por tanto nos queda:
3. La base tiene a un número diferente de 0 comprendido entre -1 y 1 y el exponente a +∞ . En este caso el límite es 0.
Ejemplo:
4. La base tiende a un número negativo menor o igual que -1 y el exponente a +∞ . En este caso el límite no existe, pues los productos son alternativamente de signo contrario.
Ejemplo:
5. En el caso en que la base tiende a 1 y el exponente a +∞ tenemos una indeterminación que se resuelve aplicando la fórmula:
Ejemplo:
Aplicando la fórmula debemos encontrar el exponente de  :
:
Ahora si reemplazando en la fórmula tenemos que:
PREGUNTA: Para desarrollar
FUNCIONES CONTINUAS Y DISCONTINUAS
Una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, si no presenta puntos de discontinuidad.
Se dice que una función es continua si existe continuidad para todos y cada uno de los puntos de su dominio.
Continuidad en un punto:Una función f(x) se dice que es continua en un punto a (x=a) si se verifica que:
Continuidad en un intervalo: Una función y=f(x)se dice continua en un intervalo si es continua en todos y cada uno de los puntos del intervalo.
Para profundizar este tema ingresa a la presentación del recurso web propuesto para este tema.
PREGUNTA: ¿Cuál de las siguientes funciones no es continua?
FUNCIONES DISCONTINUAS
Una función es discontinua si tiene puntos en los cuales una pequeña variación de la variable independiente produce un salto en los valores de la variable dependiente. A estos puntos se les denomina puntos de discontinuidad.
Los puntos de discontinuidad pueden ser de dos tipos:
- Puntos en los que la función no está definida, es decir, los puntos que no pertenecen al dominio de la función.
- Puntos en los que la gráfica presenta un salto.
Una función se dice que es discontinua en a si f(x) no es continua para x=a
Cuando una función es discontinua interesa distinguir dos posibilidades:
- Si no existe el
 , se dice que la discontinuidad es esencial.
, se dice que la discontinuidad es esencial. - Si existe el
 , se dice que la discontinuidad es evitable.
, se dice que la discontinuidad es evitable.
En este caso, se presentan dos posibilidades: que f(a) no exista o que  .
.
Para conseguir que una función con discontinuidad evitable sea continua, se altera en f(x) solamente su posible valor para x=a de manera que pase a ser f(a)=L, generalmente por métodos de factorización. Al hacer esto, se dice que se ha evitado la discontinuidad en a.
PROCEDIMIENTO PARA DETERMINAR DISCONTINUIDAD EN FUNCIONES
Para saber si la función es discontinua se realiza el siguiente procedimiento:
1. Identificar los puntos singulares que son los valores de x que hacen que el denominador se anule.
2. Hallar el límite de la función en ese punto singular:
a. Si el límite no existe o es infinito entonces la función es discontinua.
Si el límite existe hay que compararlo con el valor asignado a la función en ese punto.
b. Si el límite y el punto singular son iguales entonces la función es continua.
c. Si los puntos singulares y el limite son distintos la función es discontinua. En este caso se dice que es una discontinuidad evitable.
Ejemplo 1:
1. Identificar los puntos singulares que son los valores de x que hacen que el denominador se anule.
El denominador es x-1 que se anula para x=1.
El punto singular es x=1.
2. Hallar el límite de la función en ese punto singular:
Desarrollamos el producto notable 
Observamos que el los punto singular y el limite son distintos la función es discontinua y la discontinuidad es evitable.
Ejemplo 2:
Determinar si la función  es continua o discontinua.
es continua o discontinua.
El denominador es  que se anula para dos valores de x. Para averiguarlos se debe hallar las raíces de la función cuadrática
que se anula para dos valores de x. Para averiguarlos se debe hallar las raíces de la función cuadrática 
Probamos con los dos valores hallando el límite. Para 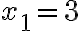
Desarrollamos el producto notable y el trinomio:
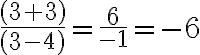 El límite es distinto al punto singular luego hay discontinuidad evitable.
El límite es distinto al punto singular luego hay discontinuidad evitable.
Ahora probamos con los dos valores hallando el límite. Para 
Desarrollamos el producto notable y el trinomio:
 El límite no existe, la función es discontinua.
El límite no existe, la función es discontinua.
ESTO SIGNIFICA QUE LA FUNCIÓN  ES DISCONTINUA.
ES DISCONTINUA.
Ejemplo 3:
Mostrar que presenta una discontinuidad evitable para 
Solución:
Si  no está definida. Para
no está definida. Para  se tiene que:
se tiene que:
Como existe este límite pero no existe f(1), la función tiene una discontinuidadevitable en x=1.
Luego: redefinimos 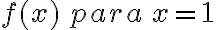 . Definimos
. Definimos  y convertimos la función f en una función continua.
y convertimos la función f en una función continua.
Redefinición:
PREGUNTA: La discontinuidad es la función  es?
es?
Concepto de la derivada
La derivada es uno de los conceptos más importantes en matemáticas. La derivada es el resultado de un límite y representa la pendiente de la recta tangente a la gráfica de la función en un punto.
Entonces como vimos anteriormente se define como:
Observemos la siguiente gráfica para determinar qué significa cada uno de éstos términos de la fórmula anterior:
La derivada de una función f(x) se puede denotar de varias formas:
La notación que utilizaremos para continuar con el curso será f'(x)
PREGUNTA: Derivada de una función es lo mismo que decir:
FÓRMULAS DE DERIVACIÓN
Ahora, simplificaremos el procedimiento para determinar la pendiente de la recta tangente a un punto o llamada DERIVADA.
Aplicar la fórmula de límite para obtener la derivada de una función resulta extenso y tedioso, así que veremos que existen fórmulas definidas, exactas y sencillas para obtener de forma directa la derivada de una función sea una función constante, un producto de funciones, un cociente de funciones, etc.
FORMULAS BÁSICAS DE DERIVACIÓN: Imprimir recurso word: Derivadas comunes
DERIVADA DE UNA FUNCIÓN CONSTANTE
Sea f(x)=a
Donde a es un valor constante (Número real).
Su derivada se define como:
f'(x)=0
Ejemplo: Hallar la derivada de la función f(x)=5
f'(x)=0
DERIVADA DE UNA POTENCIA
Su derivada se define como:
Ejemplo: Hallar la derivada de la función 
PREGUNTA: La derivada de la función  es:
es:
a) F’(x)=x9
b) F'(x)=9x9 c) F'(x)=9x10 d) F'(x)=10x9
DERIVADA DE SUMA Y RESTA DE FUNCIONES
Cuando tenemos funciones formadas por la suma o resta de dos o más términos, debemos determinar la derivada de cada uno de sus términos y expresar en la mínima expresión posible.
Matemáticamente tenemos que:
Ejemplo: Hallar la derivada de 
Este ejercicio se puede desarrollar de dos formas:
1. Como un producto directamente.
f'(x)=g'(x).h(x)+g(x)h'(x)
2. Desarrollando la multiplicación de los factores y luego como suma de términos.
Puedes escoger el método que se te facilite aplicar.
PREGUNTA: Calcula la derivada de 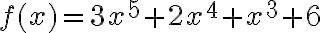
a) f'(x)=5x2+3x3+4x2 b) f'(x)=5x4+x3+3x2 c) f'(x)=15x4+8x3+3x2 d) f'(x)=5x5+4x3+2x2
DERIVADA DE PRODUCTO DE FUNCIONES (MULTIPLICACIÓN)
La derivada de un producto es igual a la derivada del primer factor por el segundo, más la derivada del segundo factor por el primero.
Matemáticamente tenemos:
Ejemplo: Hallar la derivada de la función 
Esta función la podemos escribir como producto de funciones de la siguiente manera:
f'(x)= 8x
PREGUNTA: Cuál es la derivada de la función 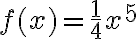
a) f'(x)=4/5x5 b) f'(x)=5/4x4 c) f'(x)=5/4x5 d) f'(x)=5/4x5
DERIVADA DE COCIENTE DE FUNCIONES (DIVISIÓN)
La derivada de un cociente es igual a la derivada del numerador por el denominador, menos el numerador por la derivada del denominador, dividido todo entre el cuadrado del denominador.
Expresado matemáticamente tenemos:
Ejemplo: Hallar la derivada de la función 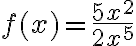
Este procedimiento también se puede realizar como derivada de un producto si lo expresamos de la forma ![g(x).[h(x)]^{-1} g(x).[h(x)]^{-1}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/0220bb272f104d50bcc0484b3bf0b513.gif)
PREGUNTA: La derivada de la función  es:
es:
a) f'(x)=20/5x9 b) f'(x)=100x9 c) f'(x)=20x9 d) f'(x)=100/9x9
DERIVADAS DE ORDEN SUPERIOR
Como la derivada de una función es otra función, entonces podemos tratar de hallar la derivada de esta nueva función. Si hacemos tal cosa, el resultado es de nuevo una función que pudiera ser a su vez derivada. Si continuamos así una y otra vez, tenemos lo que se conoce por derivadas de orden superior, que consiste en derivar el resultado de una derivación anterior.
La notación que utilizaremos para denotar derivadas de orden superior es:
Primera derivada f’(x)
Segunda derivada f"(x)
Tercera derivada es f’’’(x)
Cuarta derivada f(4)(x) y así sucesivamente.
Ejemplo: Hallar la tercera derivada de la función f(x)=6x3-5x2
f''(x)=36x-10
f'''(x)=36
Las derivadas de orden superior también son útiles en la física, cuando deseamos indagar acerca del movimiento de un objeto y obtener una medida de variación, que se logra comparando las distancias recorridas con los tiempos invertidos.
Si podemos obtener la función del desplazamiento de una partícula en función del tiempo, podemos derivar el desplazamiento respecto al tiempo para obtener la velocidad, y derivar la velocidad respecto al tiempo para obtener la aceleración de dicha partícula.
Ejemplo: El desplazamiento de una partícula está dado por la función 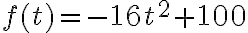 . Determinar su velocidad y aceleración en t=2seg.
. Determinar su velocidad y aceleración en t=2seg.
Aplicando derivadas de orden superior obtenemos:
Velocidad= v=f'(t)=-32t
Aceleración= a=f''(t)=-32
Ahora ya podemos determinar éstas variables en un instante dado. Si t=2seg entonces:
Su aceleración será  como es negativa decimos que es desaceleración, o sea que está deteniendo la partícula.
como es negativa decimos que es desaceleración, o sea que está deteniendo la partícula.
Su velocidad en t=2seg es  como es negativa significa que está disminuyendo la velocidad, nuevamente vemos que está frenando.
como es negativa significa que está disminuyendo la velocidad, nuevamente vemos que está frenando.
Y su desplazamiento está dado por 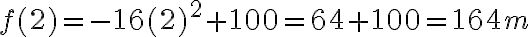 .
.
PREGUNTA: ¿Cuál es la velocidad de un automóvil que viaja de una ciudad A a una ciudad B, cuya ecuación de su desplazamiento está dada por  en el instante t=1seg?
en el instante t=1seg?
a) v=6m/s b) v=5m/s
c) v=13m/s d) v=18m/s
DERIVADAS DE LAS FUNCIONES TRIGONOMÉTRICAS
Recordemos que las funciones trigonométricas son seno (Sen), coseno (Cos), tangente (Tan), cotangente (Ctg), secante (Sec) y cosecante (Csc).
De igual forma que tenemos reglas básicas de derivación cuyas fórmulas están definidas, para estas funciones también tenemos definidas sus derivadas inmediatas:
FUNCIÓN TRIGONOMETRICA | DERIVADA |
Nótese que las funciones trigonométricas tienen entre paréntesis el ángulo, no se debe confundir con una multiplicación de una variable por una función trigonométrica como por ejemplo  .
.
PREGUNTA: Hallar la derivada de la función h(x)=xTan(x)
Nota: No olvides que debes aplicar derivada de un producto.
a) h'(x)=tanx+xsecx b) h'(x)=tanx+xcsc2x c) h'(x)=cotanx+xsecx d) h'(x)=tanx+xsec2x
REGLA DE LA CADENA O DERIVADA DE LA FUNCIÓN COMPUESTA
La regla de la cadena se utiliza cuando queremos derivar una composición de funciones.
Si f es diferenciable en x y g es una función diferenciable en f(x), entonces la función 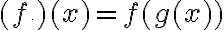 es diferenciable en x.
es diferenciable en x.
Matemáticamente se describe:
Debemos diferenciar siempre la operación más EXTERNA de la función (función elevada al cuadrado):
(f(x)) 2
(x 2 +3) 2
y la operación más interna de la función (adición de términos):
( x 2 +3 ) 2
1. Primero desarrollamos la derivada de la operación más externa que afecta la función, en este caso derivada de una potencia:
2 (x 2 +3) 1
2 (x 2 +3)
2. Desarrollamos la derivada interna y multiplicamos a la derivada externa, en este caso suma términos variable con potencia y término independiente:
y '= 2(x 2 +3)( 2x+0 )
3. Expresamos el resultado realizando las operaciones pertinentes.
Expresemos la función de una forma más entendible e identificable:
Ahora comencemos la aplicación de la regla de la cadena:
1. Primero desarrollamos la derivada de la operación más externa que afecta la función, en este caso derivada de una potencia:
3 (Tan(x))2
2. Desarrollamos la derivada interna y multiplicamos a la derivada externa, en este caso suma términos variable con potencia y término independiente:
3(Tan(x)) 2 * sec^2(x)
3. Expresamos el resultado realizando las operaciones pertinentes.
Vídeo para profundizar:
PREGUNTA: La derivada de la función  es:
es:
Nota: No olvides la regla de derivación de productos, regla de la cadena y factorización hasta la mínima expresión para solucionar este ejercicio.
a) xTan2(x) b) Sec2(x)(1+2xTan(x)) c) xSec2(x)+Tan (x) d) Sec2(x)+Tan(x)
Derivación implícita
FUNCIONES IMPLÍCITAS
Una correspondencia o una función está definida en forma implícita, cuando no aparece despejada.Es decir que la relación entre x y y viene dada por una ecuación de dos incógnitas cuyo segundo miembro es cero.
Derivadas de funciones implícitas
Para hallar la derivada en forma implícita no es necesario despejar y. Basta derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo presente que:
x=1
Por lo que omitiremos x y dejaremos y.
Ejemplo 1:
6x-2y=0
1. Derivamos entonces cada uno de los miembros:
Ejemplo 2:
1. Derivamos cada término en forma individual:
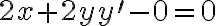 Recordemos que
Recordemos que  es lo mismo que decir
es lo mismo que decir 
Cuando las funciones son más complejas vamos a utilizar una regla para facilitar el cálculo:
![]()
Ejemplo 3:
Aplicamos la fórmula teniendo en cuenta la regla de la cadena, si es aplicable, en cada función:
![]()
Observemos que en todos los ejemplos las funciones están igualadas a 0. Este requisito es primordial.
Vídeo para profundizar:

a) y'=x2 /6y2+2y+10 b) y'=2x / 3y2+2y+1 c) y'=x / 3y2+2y+10 d) y'=2x / 2y2+3y+1
REGLA DE L’HOPITAL
Dadas dos funciones f (x) y g (x) continuas y derivables en x=c , si f (x) y g (x) tienden ambas a cero o a infinito cuando x tiende a c , entonces el límite cuando x tiende a c del cociente de f (x) y g (x) es igual al límite cuando x tiende a c del cociente de las derivadas de f(x) y g(x), siempre que este límite exista (c puede ser finito o infinito)
Expresado matemáticamente:
Entonces aplicamos la regla de L’hopital:
Esto significa que tomamos numerador y denominador y derivamos por separado.
Ejemplo:
Aplicamos la regla de L’hopital al límite original:
Derivamos tanto numerador como denominador
PREGUNTA:
Dadas las funciones  y
y 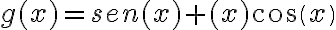 aplicar la regla de L'HOPITAL
aplicar la regla de L'HOPITAL
¿el valor del límite es?: a) 0 b) 1 c) -1 d) 2
Primitivas de una función
Dadas dos funciones f(x) y (x), definidas en un intervalo I=[a,b], diremos que F(x) es una
función primitiva de (x) si la derivada de  es la función f(x) en el intervalo I.
es la función f(x) en el intervalo I.
Ejemplo 1:
Si tenemos la función  =
= 
Entonces f(x)=2x
Significa que  es primitiva de
es primitiva de 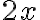 .
.
¿Cuántas primitivas puede tener una función?
Una función cualquiera admite infinitas primitivas. Dos funciones son primitivas de una misma función.
si y solo si se diferencian solo en una constante aditiva (C).
Es decir, si F(x) y G(x) son primitivas de f(x) , entonces existe un número real C, tal que
F(x)=G(x) +C
PREGUNTA:
Hallar la primitiva de la función  =
= 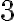
 -2x+4
-2x+4
Sugerencia: Verifica que la respuesta que escoges es la correcta, derivándola.
a) F(x)=x3-x2+4x
b) F(x)=3x3-2x2+4x+c c) F(x)=x3-x2+4x+c d) F(x)=6x-2
INTEGRAL INDEFINIDA
En la lección anterior vimos el concepto de la primitiva de una función. Esta función primitiva es la que llamamos integral.
Integración significa calcular antiderivadas o primitivas, el proceso contrario de la derivación.
La integral es un concepto utilizado para determinar el valor de las áreas debajo de curvas o rectas. En primera instancia, es importante pensar que siempre se va a poder determinar la antiderivada empleando fórmulas, igual como se hacía en el cálculo de derivadas.
La notación que utilizaremos para referirnos a dicha primitiva o antiderivada, como también se conoce será:
Las fórmulas de integración, al igual que en la derivación están definidas:
Ejemplo: Hallar la integral de la función 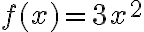
Aplicando la fórmula de integración número 1 y 2 se tiene:
PREGUNTA: Cual es la integral de la función 
a) -3x2/2+C b) 3x2/2+C c) 3x3/3+C d) 3x4/4+C
INTEGRACIÓN POR DESCOMPOSICIÓN
CASO 1: Si f(x) y g(x) son dos funciones integrables entonces: La integral de una suma o resta de funciones es igual a la suma de sus integrales tomadas por separado.
Ejemplo: Hallar la integral de la función 
Aplicando la fórmula de integración número 1y 2 se tiene:
CASO 2:
Si f(x) es una función integrable y  : La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
: La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
PREGUNTA: Halla por medio de la descomposición la expresión 
a) 2/4x4-1/3x3+3/2x2+7x+c
b) 4x4-3x3+3/2x2+7x+c
c) 1/4x4-1/3x2+3/2x2+7x+c
d) 2/4x3-1/3x2+3/2x+7
INTEGRAL DEFINIDA
La integral definida es un concepto utilizado para determinar el valor de las áreas debajo de curvas o rectas en un intervalo [a, b] en el que, para cada uno de sus puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b].
Se llama integral definida de la función entre los puntos a y b al área de la porción del plano que está limitada por la función, el eje horizontal OX y las rectas verticales de ecuaciones x = a y x = b y se denota como:
La integral definida cumple las siguientes propiedades:
· Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
· Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
· La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
· La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
· Al cambiar (invertir) los límites de una integral, ésta cambia de signo.
· Dados tres puntos tales que a < b < c, entonces se cumple que:
· Para todo punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) tales que f (x) £ g (x), se verifica que:
Ejemplo:
Hallar la integral de la función  en el intervalo [3,5]
en el intervalo [3,5]
Aplicando la fórmula de integración se tiene:
Ahora remplazamos por los valores del intervalo:
(98)+(48)+(8)=154
PREGUNTA: Cuál es el valor del área bajo la curva de la función  comprendida en el intervalo (-1,2)
comprendida en el intervalo (-1,2)
a) 21/2 b) -51/2 c) 51/2 d) -21/2
EJEMPLOS DE APLICACIÓN DE INTEGRALES
EJEMPLO PRACTICO 1:
Hallar el área del trapecio determinado por la recta de ecuación  , el eje OX, la recta
, el eje OX, la recta 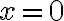 y
y  . Calcular esta área geométricamente y comprobar que coincide con el valor de la integral definida
. Calcular esta área geométricamente y comprobar que coincide con el valor de la integral definida 
=0=0
Geométricamente tenemos un trapecio: Si observamos está formado por un cuadrado de base 1 y altura 1, y un rectángulo de base 1 y altura 1. El Área de un cuadrado se define por A=base*altura y la del triangulo A=(base*altura)/2. Por tanto tenemos que el área del trapecio es:
Ahora comprobaremos por medio de la aplicación de la integral:
EJEMPLO PRACTICO 2:
Determinar el área del recinto limitado por las curvas  y
y 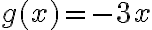 en el intervalo [-3,0].
en el intervalo [-3,0].
Realizamos la gráfica de cada una de las funciones sobre el mismo plano:
Se puede observar que el área bajo la curva se debe determinar sumando las dos áreas que resultan en la gráfica en los intervalos [-3,-2] y [-2,0].
Al plantear debemos tener en cuenta cual función limita por arriba el área a determinar y cual la limita por debajo.
Entonces:
En el intervalo [-3,-2] la función que limita por encima al área es g(x)=-3x y por debajo la limita  .
.
Sin embargo, en el intervalo [-2,0] la región está limitada superiormente por la función  e inferiormente por la función g(x)=-3x
e inferiormente por la función g(x)=-3x
Entonces planteamos:
PREGUNTA: Cuál es el valor de la integral o área bajo la curva del ejercicio práctico 2 de ésta lección:
a) 20.25 b) 32.35 c) 15.22 d) 17.25





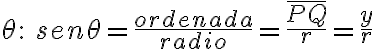



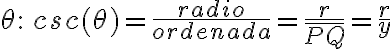

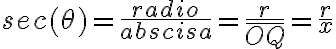



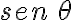


















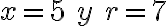




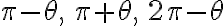






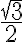










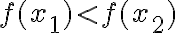
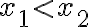



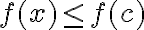


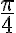



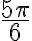
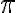
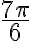



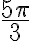

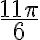
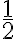

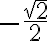

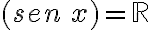
![(sen\, x)=[-1,\, 1] (sen\, x)=[-1,\, 1]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/928194399aa0f408a4673b6631c4c158.gif)

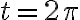
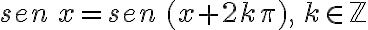



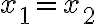
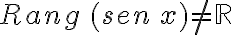


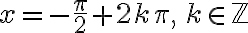
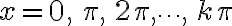

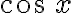

![(cos\, x)=[-1,\, 1] (cos\, x)=[-1,\, 1]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/2ffa204f0fca052f297a303118fd0cf4.gif)




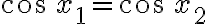



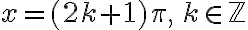
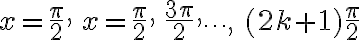





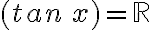





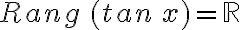

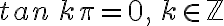

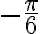






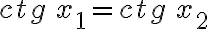
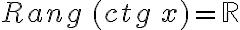






![(- \infty ,b]=\{x \epsilon \mathbb{R}| - \infty < x \leq b\} (- \infty ,b]=\{x \epsilon \mathbb{R}| - \infty < x \leq b\}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/ab09b73d7d01484d675df23a707544e2.gif)



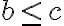


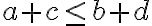





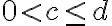








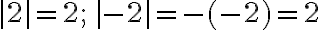

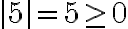
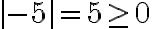



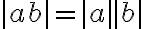


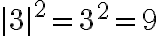







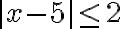
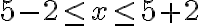
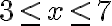



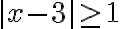
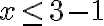
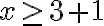

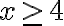
![R=(-\infty,2]U[4,\infty) R=(-\infty,2]U[4,\infty)](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e645adf63092c8b661b61a5fa7b35078.gif)





![R=[\frac{1}{2},\, 1] R=[\frac{1}{2},\, 1]](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/0297752ae45c5cd25f56c172d0a346a5.gif)





![R=(-\infty ,\, -\frac{27}{20}]\,\tiny\cup\,\Large [\frac{33}{20},\,\infty) R=(-\infty ,\, -\frac{27}{20}]\,\tiny\cup\,\Large [\frac{33}{20},\,\infty)](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/73e2ce78ae5883d19dcb7fe596a20ed2.gif)






![f\circ g=3[x^2-1]+5 f\circ g=3[x^2-1]+5](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/51010b7670eb799e797e6cf24e2998b1.gif)










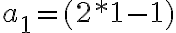





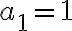
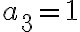
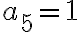

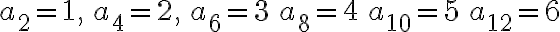

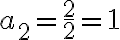





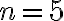




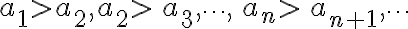
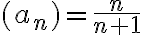

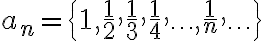

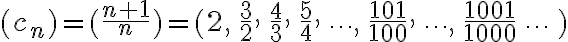

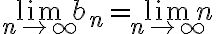

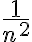





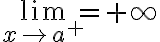


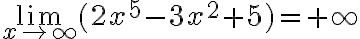

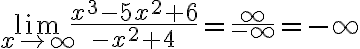
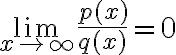














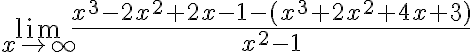





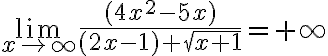












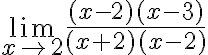
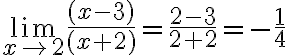


![\lim_{x \to a}[f(x)]^{g(x)} \lim_{x \to a}[f(x)]^{g(x)}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/2d4cf3c24895dd1977c50a58f77db4ab.gif)
![\lim_{x \to \infty}[f(x)]^{g(x)} \lim_{x \to \infty}[f(x)]^{g(x)}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/ecc2d35fd98318ccc269fedfefcbfda8.gif)
![\lim_{x \to 1}[x+1]^{2x-3} \lim_{x \to 1}[x+1]^{2x-3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b03c1bc261fa8404c723593652dd1ece.gif)
![[1+1]^{2(1)-3} [1+1]^{2(1)-3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/01029a53a15d3064749c00b45026915e.gif)
![[2]^{-1}=\frac{1}{2} [2]^{-1}=\frac{1}{2}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/02ccdc0b13d14f97c4994b8dd76a35e5.gif)
![\lim_{x \to \infty}[\frac{2x+1}{1+x}]^{2x-3} \lim_{x \to \infty}[\frac{2x+1}{1+x}]^{2x-3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/7b01b5c4a896192447c3955eeb1dbaef.gif)

![\lim_{x \to \infty}[\frac{1+x}{2x+1}]^{2x-3}=[\frac{1}{2}]^{\infty}=0 \lim_{x \to \infty}[\frac{1+x}{2x+1}]^{2x-3}=[\frac{1}{2}]^{\infty}=0](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b9804daf1468b56e8f6036b08e02d59f.gif)
![\lim_{x \to \infty}[\frac{-3x+1}{1+x}]^{2x-3}=[-3]^{\infty}= No existe \lim_{x \to \infty}[\frac{-3x+1}{1+x}]^{2x-3}=[-3]^{\infty}= No existe](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/88c2500b0a16af0cba11b289ddd2a05c.gif)
![\lim_{x \to a}[f(x)]^{g(x)}=1^\infty=e^{\lim_{x \to a}g(x)*[f(x)-1]} \lim_{x \to a}[f(x)]^{g(x)}=1^\infty=e^{\lim_{x \to a}g(x)*[f(x)-1]}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e23a684b659a28b48b98cb243382ab8b.gif)
![\lim_{x \to 0}[\frac{1+x}{2x+1}]^{\frac{2x+3}{x}} \lim_{x \to 0}[\frac{1+x}{2x+1}]^{\frac{2x+3}{x}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/e00602a30c7159d08487132536137b31.gif)
![\lim_{x \to 0}[\frac{2x+3}{x}]*{\frac{1+x}{2x+1}-1} \lim_{x \to 0}[\frac{2x+3}{x}]*{\frac{1+x}{2x+1}-1}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/fd9d45b90695e543b929ab354d1d807f.gif)
![\lim_{x \to 0}[\frac{2x+3}{x}]*{\frac{1+x-2x-1}{2x+1}} \lim_{x \to 0}[\frac{2x+3}{x}]*{\frac{1+x-2x-1}{2x+1}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/c4c74ba2ee4a2a8809b212e281f5d916.gif)
![\lim_{x \to 0}[\frac{2x+3}{x}]*{\frac{-x}{2x+1}} \lim_{x \to 0}[\frac{2x+3}{x}]*{\frac{-x}{2x+1}}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/b94b418b7491b795fd090976a85c8b7d.gif)


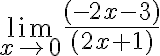

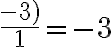
![\lim_{x \to 0}[\frac{1+x}{2x+1}]^{\frac{2x+3}{x}}=e^{-3} \lim_{x \to 0}[\frac{1+x}{2x+1}]^{\frac{2x+3}{x}}=e^{-3}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/20cf81baf11ff4740ae11ea23e37e946.gif)
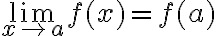
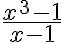

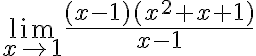
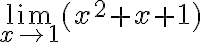



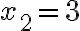


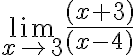
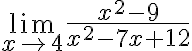



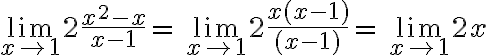


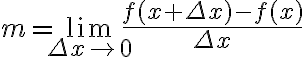


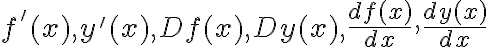








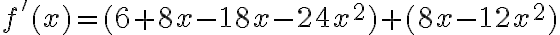
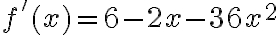
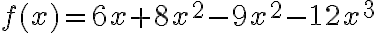


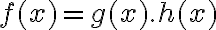





![f'(x)=\frac{g'(x).h(x)-g(x).h'(x)}{[h(x)]^2} f'(x)=\frac{g'(x).h(x)-g(x).h'(x)}{[h(x)]^2}](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/75808b1a8a46facd0bfc627f47f0efca.gif)
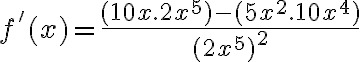

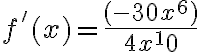
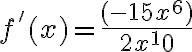
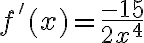
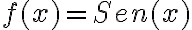


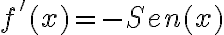



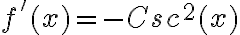

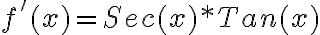





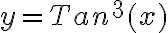

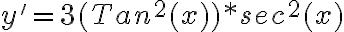















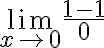




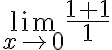
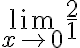





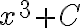
![\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x) dx \int [f(x)+g(x)]dx=\int f(x)dx+\int g(x) dx](https://bachilleratoenlinea.com/educar/filter/tex/pix.php/740c0912308a3cdf34e39ed4c03a814a.gif)



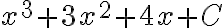




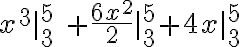
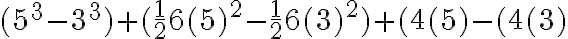


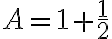


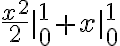
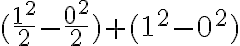
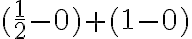
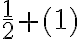

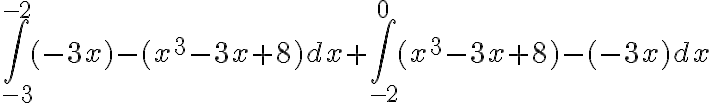




Comentarios
Publicar un comentario