FÍSICA 9º y 10º
MAURICIO MUÑOZ MATEMÁTICO FÍSICO UNIVALLE
Ella es única,; pero la multiplicidad de los hechos y los límites de nuestra inteligencia y necesidades pedagógicas en último término, la obligan a dividirse en varias ramas:
- Astronomía: se ocupa del estudio de los cuerpos celestes, sus movimientos, los fenómenos ligados a ellos, su registro y la investigación de su origen a partir de la información que llega de ellos a través de la radiación electromagnética o de cualquier otro medio.
- Biología: se ocupa del estudio de los seres vivos y, más específicamente, de su origen, su evolución y sus propiedades (génesis, nutrición, morfogénesis, reproducción, patogenia, etc.).
- Física: se ocupa del estudio de las propiedades del espacio, el tiempo, la materia y la energía, teniendo en cuenta sus interacciones.
- Geología: se ocupa del estudio de la forma interior del globo terrestre, la materia que lo compone, su mecanismo de formación, los cambios o alteraciones que ésta ha experimentado desde su origen, y la textura y estructura que tiene en el actual estado.
- Química: se ocupa del estudio de la composición, la estructura y las propiedades de la materia, así como de los cambios de sus reacciones químicas.
* La fisica es la ciencia que estudia la energía y el movimiento y la química estudia la energía de la materia.
* La fisica es la ciencia que estudia la materia y sus transformaciones y la química estudia la energía de la materia.
* No hay diferencia alguna entre la física y la química, por que la dos son ciencias fundamentales.
Magnitudes fundamentales y magnitudes derivadas
MAGNITUDES FUNDAMENTALES
El objeto de toda medida es obtener información cuantitativa de una cantidad física. Para esto es necesario definir las magnitudes físicas para poder expresar los resultados de las medidas.
Las magnitudes fundamentales son las magnitudes que no pueden formularse respecto a otras magnitudes. En mecánica, tres magnitudes fundamentales son suficientes: la longitud, la masa y el tiempo. En electricidad, sumaremos una cuarta magnitud: la carga eléctrica.
Longitud
La unidad de longitud es el metro. Dos de los patrones de referencia más conocidos o aceptados son:
El metro es la longitud del prototipo internacional conservado en Sèvres, cerca de París.
El metro es la distancia igual a 1650763,73 longitudes de onda, en el vacío, de una cierta rdiación roja del gas criptón 86.
Masa
Admitiremos que a cada sistema material, se puede hacer corresponder un número positivo llamado masa y que tenga la siguiente propiedad: la masa de un sistema es la suma de las masas de sus partes. La unidad de masa es el kilogramo. Dos conocidos puntos de referencia con respecto al kilogramo son:
La masa de un litro de agua a 4ºC.
Un Kilogramo es la masa del prototipo internacional conservado en Sèvres, cerca de París
Tiempo
La unidad de tiempo es el segundo. Los parámetros de referencia aceptados son:
El segundo es la fracción  de la duración del año tropical de 1900. El año tropical comprende 365,24219879 días.
de la duración del año tropical de 1900. El año tropical comprende 365,24219879 días.
Un segundo es igual a 9.192.631.770 períodos de radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del isótopo 133 del átomo de cesio (133Cs), medidos a 0° Kelvin.
MAGNITUDES DERIVADAS
Las magnitudes derivadas se obtienen de las magnitudes fundamentales, por medio de ecuaciones matemáticas. Algunos ejemplos de esto son la superficie (derivada de la longitud, de dimensión 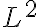 ), el volumen (derivada de la longitud, de dimensión
), el volumen (derivada de la longitud, de dimensión  ), la velocidad (que corresponde a la longitud de un recorrido divida en el tiempo tomado para atravesarla, de dimensión
), la velocidad (que corresponde a la longitud de un recorrido divida en el tiempo tomado para atravesarla, de dimensión  ), La aceleración (que corresponde a una longitud dividida en el tiempo al cuadrado, de dimensión
), La aceleración (que corresponde a una longitud dividida en el tiempo al cuadrado, de dimensión  ), etc.
), etc.
En una ecuación de cantidades físicas, las dimensiones de las expresiones puestas en cada miembro deben ser las mismas; esto es evidente, porque estamos igualando cantidades de la misma especie, es decir del mismo tipo.
En la ecuación s=vt si la dimensión de s es L, necesariamente la dimensión de (vt) será también L para que la ecuación sea coherente. En este caso se dice que la ecuación es homogénea en sus dimensiones.
En el siguiente vídeo se observa la explicación de las magnitudes básicas y derivadas con ejemplos prácticos
PREGUNTA: Son magnitudes fundamentales
a) Longitud, velocidad y aceleración.
b) Longitud, masa y tiempo.
c) Masa, aceleración y tiempo.
d) Longitud, área y volumen.
La notación científica es un modo conciso de representar un número utilizando potencias de base diez. Esta notación se utiliza para poder expresar fácilmente números muy grandes o muy pequeños.
Los números se escriben como un producto:
siendo:
un número entero o decimal mayor o igual que 1 y menor que 10, que recibe el nombre de coeficiente.
un número entero, que recibe el nombre de exponente u orden de magnitud.
La notación científica utiliza un sistema llamado coma flotante, o de punto flotante en países de habla inglesa y en algunos hispanohablantes.
Para convertir un número, ya sea entero o decimal, en notación científica se realiza lo siguiente:
| Número | 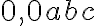 | 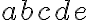 |
| Dirección de la coma | → | ← |
| Signo de n |  |  |
| Ejemplo |  X 10-4 X 10-4 |  X 104 X 104 |
Cuando corremos la coma hacia la derecha, el signo del exponente es negativo y cuando la corremos hacia la izquierda el signo es positivo; de igual forma cuando el valor del número d es mayor o igual que 6, se puede aproximar el valor de c a un punto más.
Ejemplos: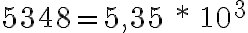 observamos que el punto decimal corrió a la izquierda 3 cifras por tanto el exponente es 3 y es positivo.
observamos que el punto decimal corrió a la izquierda 3 cifras por tanto el exponente es 3 y es positivo. observamos que el punto decimal corrió a la izquierda 8 cifras por tanto el exponente es y es positivo.
observamos que el punto decimal corrió a la izquierda 8 cifras por tanto el exponente es y es positivo.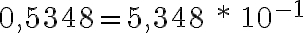 observamos que el punto decimal corrió a la derecha 1 cifras por tanto el exponente es 1 y es negativo.
observamos que el punto decimal corrió a la derecha 1 cifras por tanto el exponente es 1 y es negativo. observamos que el punto decimal corrió a la izquierda 3 cifras por tanto el exponente es 3 y es positivo.
observamos que el punto decimal corrió a la izquierda 3 cifras por tanto el exponente es 3 y es positivo. observamos que el punto decimal corrió a la derecha 3 cifras por tanto el exponente es 3 y es negativo.
observamos que el punto decimal corrió a la derecha 3 cifras por tanto el exponente es 3 y es negativo.
Algunas veces, se desea conocer un valor aproximado y redondeado de una longitud de física, es decir conocer su orden de magnitud: se define como la potencia de 10 mas cercana a la magnitud.
Ejemplos: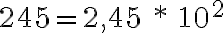 tiene por orden de magnitud
tiene por orden de magnitud 
 tiene por orden de magnitud
tiene por orden de magnitud 
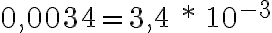 tiene por orden de magnitud
tiene por orden de magnitud 
 tiene por orden de magnitud
tiene por orden de magnitud 
Cifras significativas
Se denominan cifras significativas a todos aquellos dígitos de un número que se conocen con seguridad (o de los que existe una cierta certeza), o dicho de otra manera, son los dígitos de un número que consideramos no nulos.
Veamos unos ejemplos para entender mejor el concepto:
PREGUNTA: ¿Cuál es el aproximado en notación científica del número 8123001001?
Sistemas de referencia
Los sistemas de referencia se emplean para describir la posición y el movimiento de los cuerpos. Un sistema de referencia está formado por:
- Un punto tomado como origen de referencia de coordenadas.
- Unos ejes de coordenadas. Los ejes se cortan en el origen de referencia.
Para señalar la posición de un cuerpo indicamos la distancia hasta cada eje, y para definir su movimiento señalamos cómo cambia esta distancia con el tiempo.
Un sistema de referencia espacial indica, de manera precisa, dónde se encuentra el cuerpo en un instante determinado.
La coordenada x toma el valor de la distancia que separa la posición del cuerpo de la marca cero del eje X. Su valor será positivo o negativo dependiendo, igual que antes, de la situación del cuerpo con respecto a la marca cero.
Un sistema de referencia temporal indica, de manera precisa, en qué momento está el cuerpo en una posición concreta.
Sistemas de referencia de una dimensión
Sobre una recta orientada de -x hacia x (figura a) se toma un punto fijo 0 como origen de una graduación que será positiva a la derecha de 0 y negativa a la izquierda de 0. Se dice que esta recta es un espacio de una dimensión.
Figura a
Sistema de coordenadas de dos dimensiones
El plano es un espacio de dos dimensiones. Sobre un plano se dibujan dos rectas orientadas -x a x "y" -y a y rectangulares, llamadas ejes de coordenadas, que se cortan en el punto 0 u origen. El plano queda dividido en 4 cuadrantes: I, II, III y IV como se ve en la figura b.
Figura b
Siempre que se desea indicar un punto en el plano de dos dimensiones se denota como (x,y)
c) Sistema de coordenadas de tres dimensiones
En el espacio ordinario, en donde vivimos, se dibujan tres rectas orientadas rectangulares de origen común.
Figura c
De donde, cualquier punto del espacio se define por tres números (x,y,z).
Imaginemos estar en una habitación, si nos paramos en una esquina podemos identificar que las paredes nos forman los planos "xy" y "yz" y el piso sería el plano "xy".
PREGUNTA: ¿Para qué se emplean los sistemas de referencia?
Video: El metodo cientifico. Explicación para alumnos de secundaria
Es todo aquello que puede ser medido, y se puede representar por un número, además pueden ser estudiados en las ciencias experimentales.
¿Qué es una Magnitud Física?
Cuando las magnitudes se pueden medir mediante un instrumento de medida, se dice que dichas magnitudes son magnitudes físicas.
Aquí tenemos algunas magnitudes físicas: la velocidad, la temperatura, la fuerza, etc.
Clasificación de las Magnitudes
Las magnitudes se clasifican en dos grandes grupos y son:
Magnitudes por su Origen:
a) Magnitudes Fundamentales
b) Magnitudes Derivadas
c) Magnitudes suplementarias o Auxiliares
Magnitudes por su Naturaleza:
a) Magnitudes escalares
b) Magnitudes vectoriales
c) Magnitudes tensoriales
Magnitudes Físicas
Escalares y vectores
Magnitudes escalares: Son aquellas que quedan totalmente determinadas dando un sólo número real y una unidad de medida.
Ejemplos de este tipo de magnitud son la longitud de un hilo, la masa de un cuerpo o el tiempo transcurrido entre dos sucesos. Se las puede representar mediante segmentos tomados sobre una recta a partir de un origen y de longitud igual al número real que indica su medida. Otros ejemplos de magnitudes escalares son la densidad; el volumen; el trabajo mecánico; la potencia; la temperatura.
Magnitudes vectoriales: No se las puede determinar completamente mediante un número real y una unidad de medida.
Por ejemplo, para dar la velocidad de un móvil en un punto del espacio, además de su intensidad se debe indicar la dirección del movimiento y el sentido de movimiento en esa dirección. Al igual que con la velocidad ocurre con las fuerzas: sus efectos dependen no sólo de la intensidad sino también de las direcciones y sentidos en que actúan. Otros ejemplos de magnitudes vectoriales son la aceleración; la cantidad de movimiento; el momento angular. Para representarlas hay que tomar segmentos orientados, o sea, segmentos de recta cada uno de ellos determinado entre dos puntos extremos dados en un cierto orden.
Se llama vector a todo segmento orientado. El primero de los puntos que lo determinan se llama origen y el segundo, extremo del vector. La recta que contiene al vector determina la dirección del mismo y la orientación sobre la recta, definida por el origen y el extremo del vector, determina su sentido.
Se denomina módulo o magnitud de un vector a la longitud del segmento orientado que lo define. El módulo de un vector es siempre un número positivo.Será representado mediante la letra sin negrita o como vector entre barras : mód v = v = |v|.
Igualdad de Vectores
Dos vectores son iguales cuando tienen el mismo módulo y la misma dirección y sentido.
Dos vectores se llaman opuestos, si tienen igual magnitud y dirección opuesta.
 ó
ó 
PREGUNTA: Las magnitudes vectoriales están caracterizadas por:
Operaciones con vectores en una y dos dimensiones
VECTORES EN UNA DIMENSIÓN
La suma de vectores:
Cuando necesitamos realizar suma de vectores en una dimensión podemos encontrarnos con dos casos:
1. Los vectores tienen la misma dirección:
En este caso la suma se realiza en forma algebraica.
Ejemplo 1:
Observemos la figura anterior:
Sea  y
y 
El vector suma será:  =
= 
2. Los vectores tienen diferente dirección: La suma de dos vectores A y B se define aplicando la regla del paralelogramo.
Primero debemos transladar los vectores de manera que el final del vector  (donde se encuentra la punta de la flecha de A) coincida con el inicio del vector
(donde se encuentra la punta de la flecha de A) coincida con el inicio del vector  (el extremo donde no está la punta de la flecha del vector B). La suma o vector
(el extremo donde no está la punta de la flecha del vector B). La suma o vector  es aquél que se trace desde el inicio del vector
es aquél que se trace desde el inicio del vector  hasta el final del vector
hasta el final del vector  . Veamos la gráfica:
. Veamos la gráfica:
La suma de varios vectores se efectúa empezando a sumar dos vectores y el resultado con el tercero y así sucesivamente.
Cuando los vectores son perpendiculares, se suman utilizando el teorema de pitágoras:




Diferencia o resta de vectores:
Tenemos los dos casos presentados en la suma de vectores:
1. Los vectores tienen la misma dirección:
Queremos efectuar la operación A - B. Remplazamos por: A + (-B) = D.
Ejemplo 2:
Sea  y
y 
El vector diferencia será:  =
= 
Luego obtendremos un vector de magnitud 2 en sentido contrario a A y a B.
2. Los vectores tienen diferente dirección:
Queremos efectuar la operación A - B = D que podemos remplazar por: A + (-B) = D. Así, nuestra diferencia fue remplazada por la suma de A y el opuesto de B.
Componentes de un vector
Sea un sistema de referencia, compuesto de dos ejes perpendiculares "x" y "y", tenemos un vector A.
Llamamos componentes a la proyección del vector A en la dirección  (
( )y de A en la dirección
)y de A en la dirección  (
( ).
).
Por el origen y por el extremo de A, completamos un triángulo rectángulo cuyos catetos son paralelos a los ejes.
Por el torema de pitágoras se calcula la magnitud del vector  :
: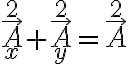

La dirección del vector  es el ángulo que forma con respecto al eje
es el ángulo que forma con respecto al eje  .
.
PREGUNTA: Al sumar los vectores  de la figura, su magnitud S es:
de la figura, su magnitud S es:
Magnitudes Escalares y Vectoriales:
Las magnitudes escalares son aquellas que quedan totalmente determinadas dando un sólonúmero real y una unidad de medida. Ejemplos de este tipo de magnitud son la longitud de un hilo, la masa de un cuerpo o el tiempo transcurrido entre dos sucesos.las magnitudes escalares están representadas por el ente matemático más simple, por un número.Podemos decir que poseen un módulo, pero que carecen de dirección.Se las puede representar mediante segmentos tomados sobre una recta a partir de un origen y de longitud igual al número real que indica su medida. Otros ejemplos de magnitudes escalares son la densidad; el volumen; el trabajo mecánico; la potencia; la temperatura. Su valor puede ser independiente del observador(v.g.: la masa, la temperatura, la densidad, etc.) o depender de la posición (v.g.: la energía potencial), o estado de movimiento del observador (v.g.: la energía cinética).En el mundo físico podemos encontrar bastantes magnitudes. Las más frecientes son las escalares como lo son:
* la temperatura,
* el tiempo.
* la masa
* la energía
* Intensidad de corriente eléctrica.
* Cantidad de sustancia
* Intensidad luminosa
* superficie
* volumen
* densidad
* frecuencia
* Potencia
Las magnitudes vectoriales no se las puede determinar completamente mediante un número real y una unidad de medida. Por ejemplo, para dar la velocidad de un móvil en un punto del espacio, además de su intensidad se debe indicar la dirección del movimiento (dada por la recta tangente a la trayectoria en cada punto) y el sentido de movimiento en esa dirección (dado por las dos posibles orientaciones de la recta). Al igual que con la velocidad ocurre con las fuerzas: sus efectos dependen no sólo de la intensidad sino también de las direcciones y sentidos en que actúan. Otros ejemplos de magnitudes vectoriales son la aceleración; el momentum o cantidad de movimiento; el momentum angular. Para representarlas hay que tomar segmentos orientados, o sea, segmentos de recta cada uno de ellos determinado entre dos puntos extremos dados en un cierto orden.Definición 1: Se llama vector a todo segmento orientado. El primero de los puntos que lo determinan se llama origen y el segundo extremo del vector. La recta que contiene al vectordetermina la dirección del mismo y la orientación sobre la recta, definida por el origen y elextremo del vector, determina su sentido.
Las magnitudes vectoriales no se las puede determinar completamente mediante un número real y una unidad de medida. Por ejemplo, para dar la velocidad de un móvil en un punto del espacio, además de su intensidad se debe indicar la dirección del movimiento (dada por la recta tangente a la trayectoria en cada punto) y el sentido de movimiento en esa dirección (dado por las dos posibles orientaciones de la recta). Al igual que con la velocidad ocurre con las fuerzas: sus efectos dependen no sólo de la intensidad sino también de las direcciones y sentidos en que actúan. Otros ejemplos de magnitudes vectoriales son la aceleración; el momentum o cantidad de movimiento; el momentum angular. Para representarlas hay que tomar segmentos orientados, o sea, segmentos de recta cada uno de ellos determinado entre dos puntos extremos dados en un cierto orden.Definición 1: Se llama vector a todo segmento orientado. El primero de los puntos que lo determinan se llama origen y el segundo extremo del vector. La recta que contiene al vectordetermina la dirección del mismo y la orientación sobre la recta, definida por el origen y elextremo del vector, determina su sentido.
A continuación, viene una guía con muchos ejercicios de vectores, resolveremos algunos en el video que viene líneas abajo.
A continuación, viene una guía con muchos ejercicios de vectores, resolveremos algunos en el video que viene líneas abajo.
Video Vectores y Escalares
MOVIMIENTO UNIFORME (M.R.U.)
Movimiento rectilíneo:
Posición de una partícula.
POSICIÓN DE UNA PARTÍCULA
Posición de una partícula
La posición de un cuerpo, considerado como una partícula, sobre una recta, es determinada por la distancia del punto respecto a un punto origen.
Si esta posición permanece invariable al transcurrir el tiempo, es decir, si la distancia del punto al origen es constante, diremos que el cuerpo se encuentra en reposo con respecto al origen.
Si esta posición varía con el tiempo, es decir, si la distancia del punto respecto al origen varía en función del tiempo, diremos que el cuerpo está en movimiento con respecto al origen y evidentemente con respecto a todos los cuerpos en reposo con el origen.
Tanto el reposo como el movimiento son relativos respecto al punto de origen escogido. Significa que un cuerpo puede encontrarse en reposo con respecto a un segundo cuerpo y, al mismo tiempo, encontrarse en movimiento con respecto a un tercero.
Las unidades de posición o de desplazamiento son el m, cm, Km., es decir, que son unidades de LONGITUD.
Ejemplo: Una persona dentro de un ascensor en movimiento, esta en reposo con respecto al ascensor, pero está en movimiento con respecto al suelo.
En conclusión, es fijando el origen como se sabe si un cuerpo está en reposo o en movimiento. Si no se menciona el origen, se subentiende que es un origen fijo sobre la tierra.
Puede haber tiempos negativos como, por ejemplo, las cuentas regresivas antes de la hora 0 del lanzamiento de un satélite.
Matemáticamente, diremos que el vector posición es una función del tiempo y escribiremos:
Ejemplo 1
Sobre una recta, un cuerpo tiene una posición dada por la ecuación:
Donde  está expresada en
está expresada en  y tiempo
y tiempo 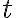 en horas.
en horas.
Para 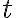 |  |
Para  | 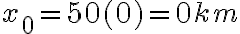 |
Para 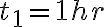 |  |
Para  | 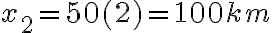 |
Podemos observar que para  la posición es
la posición es  , es decir que el cuerpo está en el origen y ésta es su posición inicial.
, es decir que el cuerpo está en el origen y ésta es su posición inicial.
A medida que aumenta el tiempo el cuerpo cambia de posición y se aleja del origen.
Si una partícula se desplaza de un posición inicial  a una posición final
a una posición final  , el desplazamiento estará dado por el vector:
, el desplazamiento estará dado por el vector:
Y podemos decir que ese desplazamiento o cambio de posición se efectuó en un intervalo de tiempo:
El símbolo  (se lee delta) significa variación.
(se lee delta) significa variación.
Ejemplo 2
Sobre una recta, un móvil tiene posición dada por la ecuación:
Donde x está expresado en m y tiempo t, en seg.
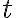 |  |
 |  |
 |  |
 | 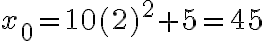 |
Para  tenemos que la posición inicial es a 5 metros del origen. Esto significa que el móvil inicia su movimiento a 5 m respecto al origen de coordenadas.
tenemos que la posición inicial es a 5 metros del origen. Esto significa que el móvil inicia su movimiento a 5 m respecto al origen de coordenadas.
El desplazamiento  en el intervalo de tiempo
en el intervalo de tiempo  seg es
seg es  .
.
PREGUNTA: Sobre una calle, un automóvil tiene una posición dada por la ecuación  (x en km y t en horas), ¿En
(x en km y t en horas), ¿En 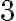 horas cuál es su posición?
horas cuál es su posición?
Movimiento rectilíneo: Velocidad de una partícula
VELOCIDAD DE UNA PARTÍCULA
Velocidad de una partícula
La velocidad es una magnitud física de carácter vectorial que expresa el desplazamiento de un objeto por unidad de tiempo.
a) Velocidad media
La velocidad media o velocidad promedio informa sobre la velocidad en un intervalo de tiempo dado. Se calcula dividiendo el desplazamiento en el tiempo requerido para efectuarlo.
La barra sobre v significa valor medio.
Una velocidad positiva indica que el cuerpo se desplaza en la dirección positiva de la trayectoria. Una velocidad negativa indicara lo contrario.
Las unidades de velocidad son el m/seg, cm/seg, km/seg, es decir, unidades de 
Ejemplos:
1. Sobre una línea recta, un auto recorre 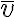 ?
?
El vector velocidad media está en la dirección del movimiento y vale 
b) Velocidad instantánea
La velocidad media no describe el movimiento en cada instante, por tanto no es adecuada para una descripción del movimiento.
La velocidad instantánea permite conocer la velocidad de un móvil que se desplaza sobre una trayectoria cuando el intervalo de tiempo es infinitamente pequeño, siendo entonces el espacio recorrido también muy pequeño, representando un punto de la trayectoria.
En forma vectorial, la velocidad instantánea es la derivada del vector posición, r con respecto al tiempo, t.
Por ejemplo:
Si un auto recorre sin parar, de una manera uniforme, una ruta de
El único medio de conocer el movimiento de un cuerpo, en cada instante, es medir su velocidad media para desplazamientos muy pequeños durante intervalos de tiempo muy pequeños a cada momento.
Tomemos otro ejemplo:
Un corredor olímpico recorre
Encontramos:
Distancias (m) | 100 | 50 | 10 | 2 | 1 |
Tiempo (seg) | 10.0 | 4.17 | 0.81 | 0.18 | 0.08 |
Velocidad media (m/seg) | 10 | 12.0 | 12.3 | 12.5 | 12.5 |
Queremos saber ahora , ¿Cuál es la velocidad del corredor exactamente sobre la raya final?
Se nota que si los desplazamientos y los intervalos de tiempo son cada vez más pequeños, la velocidad media se acerca a un valor que no varía mucho y que aquí es 12,5 m/seg. En otras palabras, se dice que la velocidad media llega a un límite.
Si a partir de esta posición y de cierto tiempo, se efectúa un desplazamiento muy pequeño, el intervalo de tiempo lo será también. Podemos definir el vector velocidad instantánea o, simplemente, velocidad a un momento dad, a la razón del desplazamiento, al intervalo de tiempo correspondiente, cuando este tiende a cero.
Nota: Para solucionar ejercicios más adelante utilizaremos el concepto de velocidad media.
PREGUNTA: Un auto recorre 5000 metros en 60 minutos. ¿Cuál es la velocidad media de dicho auto, expresada en m/s?
A) 83.3 m/min. B) 1.38 m/min. C) 1.38 m/s. D) 83.3 m/s
MOVIMIENTO RECTILÍNEO UNIFORME
La característica de este movimiento rectilíneo uniforme es que su velocidad v es constante.
a) Velocidad
Siendo la velocidad instantánea constante, necesariamente, la velocidad media es también constante e igual a v.
b) Aceleración
Según la definición de aceleración media en la lección anterior si la velocidad es constante la aceleración es 0.
c) Posición
Según la definición de velocidad media, tenemos:
Tomaremos como condición inicial que al tiempo  , la posición inicial es
, la posición inicial es  . En consecuencia.
. En consecuencia.
En resumen, las ecuaciones cinemáticas del movimiento rectilíneo uniforme son:
Ejemplo:
Un auto parte del origen con velocidad constante de 3m/seg.
a) ¿Cuál es la ecuación de su posición? Como es un movimiento uniforme, la ecuación es de la forma:
Por tanto, tenemos:
b) ¿Qué distancia recorre en 4 seg.? Aplicando la ecuación anterior, se tiene:
Ejemplo 2:
Determinar el instante y la posición en el que dos cuerpos que se mueven sobre el mismo eje se encuentran. Determinar también las velocidades de cada uno en el momento del encuentro.Las ecuaciones de la posición de cada uno están dadas por:
 Las distancias se dan en m y los tiempos en seg.
Las distancias se dan en m y los tiempos en seg.
Para solucionar este ejercicio debemos concluir que en el momento en que se encuentran, su posición será la misma. Entonces igualamos sus ecuaciones de posición:
Teniendo el tiempo reemplazamos en cualquiera de las dos ecuaciones para determinar la posición (hemos resuelto un sistema de ecuaciones con dos incógnitas):
x=3-2
x=1
La respuesta es que la posición del encuentro es x=1m y  .
.
Ahora veamos sus velocidad observando la fórmula cinemática de MRU (movimiento rectilíneo uniforme) de posición:
Para el primer móvil:
 la velocidad es el coeficiente que acompaña a
la velocidad es el coeficiente que acompaña a 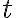 luego,
luego,  .
.
Para el segundo móvil:
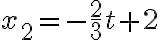 la velocidad es el coeficiente que acompaña a
la velocidad es el coeficiente que acompaña a 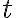 luego,
luego,  .
.
PREGUNTA: ¿Determinar el instante y la posición del encuentro de dos móviles cuyas ecuaciones de posición son:
Movimiento rectilíneo: Aceleración de una partícula
ACELERACIÓN
Muchas personas piensan que cuando un cuerpo se mueve con una gran velocidad, su aceleración también es grande; que si se mueve con poca velocidad es porque su aceleración es pequeña; y si su velocidad es cero, entonces su aceleración también debe valer cero. Esto es un error
La aceleración es una magnitud vectorial que relaciona los cambios en la velocidad con el tiempo que tardan en producirse, es decir, mide qué tan rápidos son los cambios de velocidad:
→ Una aceleración grande significa que la velocidad cambia rápidamente.
→ Una aceleración pequeña significa que la velocidad cambia lentamente.
→ Una aceleración cero significa que la velocidad no cambia, permanece constante.
Tipos de aceleración:
Aceleración tangencial: Relaciona la variación de la rapidez con el tiempo.
Aceleración normal (o centrípeta): Relaciona los cambios de la dirección con el tiempo, ocurre en movimientos curvilíneos, como por ejemplo cuando colocamos una piedra en el extremo de una cuerda y la hacemos girar.
Como estamos refiriéndonos a movimientos rectilíneos hablaremos únicamente de la aceleración tangencial o solamente nos referimos a ACELERACIÓN.
ACELERACIÓN TANGENCIAL
Una característica de los cuerpos acelerados es que recorren diferentes distancias en intervalos regulares de tiempo:
veamos este ejemplo: Sean los siguientes los datos de un movimiento de caída libre en donde lanzamos una piedra desde lo alto de un edificio:
Intervalo | Rapidez media | Distancia recorrida | Distancia total |
0 - 1 s | 5 m/s | 5 m | 5 m |
1 s - 2 s | 15 m/s | 15 m | 20 m |
2 s - 3 s | 25 m/s | 25 m | 45 m |
3 s - 4 s | 35 m/s | 35 m | 80 m |
Observa que al ser diferente la rapidez media de cada intervalo, la distancia recorrida durante el mismo es también diferente.
Aceleración constante
La tabla anterior muestra datos de un movimiento de caída libre, donde observamos que la rapidez cambia en 10 m/s cada segundo, es decir que tiene una aceleración de  ó 10 m/s².
ó 10 m/s².
Como el cambio de la velocidad en cada intervalo es siempre el mismo ( ), se trata de un movimiento de aceleración constante o uniformemente acelerado .
), se trata de un movimiento de aceleración constante o uniformemente acelerado .
La aceleración (tangencial) media de un móvil se calcula utilizando la siguiente ecuación:
Las unidades de la aceleración dadas en el sistema internacional, que es el que utilizaremos están dadas en  .
.
La dirección del vector aceleración depende:
- De que la rapidez esté aumentando o disminuyendo.
- De que el cuerpo se mueva en la dirección + o - .
El acuerdo que tomaremos es:
Si la velocidad y la aceleración van en el mismo sentido (ambas son positivas o ambas negativas) el móvil aumenta su rapidez.
Si la velocidad y la aceleración van en sentidos contrarios (tienen signos opuestos), el móvil disminuye su rapidez.
PREGUNTA: ¿Cuál es la aceleración que se utiliza en los movimientos rectilíneos?
Movimiento uniformemente acelerado:
Caída libre
Un buen ejemplo de movimiento uniformemente acelerado es el movimiento de caída libre. La experiencia muestra que todos los cuerpos en el vacío que caen o suben se ven afectados por la ACELERACIÓN de la gravedad, la cual es aproximadamente a  (para facilitar el cálculo trabajaremos con
(para facilitar el cálculo trabajaremos con  ), y está dirigida hacia el centro de la tierra.
), y está dirigida hacia el centro de la tierra.
Por lo tanto, para el estudio del movimiento vertical de un cuerpo en el vacío, un solo conjunto de ecuaciones es suficiente y nos indica a cada instante, la posición y la velocidad del cuerpo.
Ecuaciones cinemáticas:
Veamos algunos ejemplos de aplicación:
Ejemplo 1:
Se lanza una piedra hacia arriba con una velocidad de  . Para todos los ejercicios tomaremos la aceleración de la gravedad
. Para todos los ejercicios tomaremos la aceleración de la gravedad  y dirigida hacia abajo.
y dirigida hacia abajo.
Calcular:
a) ¿A que altura sube la piedra?
Escogemos el eje x dirigido hacia arriba, por lo tanto la velocidad inicial es  mientras que la aceleración es
mientras que la aceleración es  , negativa porque va en el sentido del eje x negativo.
, negativa porque va en el sentido del eje x negativo.
Tomando  , ya que la piedra inicia el movimiento desde el origen, las ecuaciones cinemáticas se reducen a:
, ya que la piedra inicia el movimiento desde el origen, las ecuaciones cinemáticas se reducen a:
En el punto más alto, la velocidad de la piedra es  , por lo tanto
, por lo tanto  .
.
 ésta es la altura o el desplazamiento que realizó la piedra.
ésta es la altura o el desplazamiento que realizó la piedra.
b) ¿Qué tiempo tardó para llegar al punto más alto?
c) Al cabo de dos segundos, ¿cuál es la posición de la piedra?
d) Al cabo de dos segundos ¿cuál es la velocidad?
e) Al cabo de seis segundos, ¿cuál es la posición?
La posición es la misma que en c). Esto nos indica que la piedra después de pasar por la altura máxima, cae regresando a su posición inicial.
f) Al cabo de  segundos ¿cuál es la velocidad?
segundos ¿cuál es la velocidad?
La velocidad es dirigida hacia abajo.
Ejemplo 2:
Desde la cima de una torre se deja caer, sin velocidad inicial, una piedra. ¿Cuáles son las ecuaciones cinemáticas del movimiento?
Aquí, es preferible escoger el eje x hacia abajo; por tanto la aceleración de la gravedad g es positiva y vale  .
.
Inicialmente la piedra se encuentra en el origen  y en reposo
y en reposo  . Las ecuaciones cinemáticas son:
. Las ecuaciones cinemáticas son:
Reemplazando los valores conocidos tenemos las ecuaciones cinemáticas que nos solicita el problema.
Si proponemos que la altura de la torre es  , entonces podemos remplazar y encontrar los valores de velocidad de llegada al suelo
, entonces podemos remplazar y encontrar los valores de velocidad de llegada al suelo  y el tiempo de la caída
y el tiempo de la caída  .
.
NOTA: En los movimientos rectilíneos generalmente se toma la trayectoria en la dirección del eje x o y.
Cuando un vector, con aceleración  ó
ó  ó velocidad inicial
ó velocidad inicial  tiene la misma dirección de la trayectoria, su signo es positivo. Cuando el vector tiene la dirección contraria a la trayectoria, su signo es negativo.
tiene la misma dirección de la trayectoria, su signo es positivo. Cuando el vector tiene la dirección contraria a la trayectoria, su signo es negativo.
Ejemplo 3:
Se lanza una piedra hacia abajo con una velocidad de 40 m/seg. Escribir las ecuaciones del movimiento, tomando el eje x hacia abajo.
Con esta dirección del eje x, la aceleración g y la velocidad inicial son positivas; las ecuaciones son:
Si proponemos un tiempo de caída de 2 segundos, las ecuaciones anteriores nos dan la posición  y la velocidad final de la piedra
y la velocidad final de la piedra  .
.
PREGUNTA: En el problema 1, sobre el lanzamiento de la piedra. Cuál seria la posición de la piedra, al cabo de 10 segundos?
A) 10M B) -100M C) 100M D) -10M
Movimiento en un plano
MOVIMIENTO EN DOS DIMENSIONES: EL PLANO
El estudio anterior trataba de los movimientos en una dimensión. Ahora nuestro análisis será ampliado a los movimientos en dos dimensiones. La partícula se mueve en un plano y puede describir cualquier trayectoria.
Utilizaremos para este fin el concepto de vectores en un plano y de sus proyecciones sobre un sistema de coordenadas cartesianas.
Posición de una partícula
La posición de una partícula en un plano, con respecto a un sistema de referencia, se determina por medio de coordenadas (x,y), dando como primer punto la posición en el eje x, y el segundo punto la posición en el eje y.
Representemos la posición de una partícula en la coordenada (3,2) del plano:
Trayectoria de una partícula: Es la línea formada por las sucesivas posiciones por las que pasa un móvil.
Desplazamiento de una partícula: El desplazamiento de una partícula o móvil entre dos instantes queda determinado por el segmento que une las posiciones por las que pasa la partícula entre esos dos instantes.
El desplazamiento si la trayectoria es rectilínea coincide con el espacio recorrido entre dos instantes.
Veamos la gráfica:
DESPLAZAMIENTO RECTILÍNEO | DESPLAZAMIENTO CURVILÍNEO |
Velocidad de una partícula
a) Velocidad media
El vector velocidad media de la partícula será la razón del desplazamiento al intervalo correspondiente, o sea:
La magnitud de la velocidad que denominaremos rapidez se obtendrá por el teorema de Pitágoras:
Y el ángulo que forma la velocidad con el eje  se expresara así:
se expresara así:
Ejemplo 1:
a) Un cuerpo se mueve desde un punto A  hasta un punto B (0,4) en 10 segundos. ¿cuál es el vector velocidad media? (las distancias en metros).
hasta un punto B (0,4) en 10 segundos. ¿cuál es el vector velocidad media? (las distancias en metros).
El vector de desplazamiento, por teorema de Pitágoras será:
La velocidad media es  y dirigida de
y dirigida de 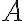 hacia
hacia 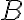 .
.
Ejemplo 2:
Sea un movimiento dado por  (distancia en
(distancia en 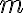 y tiempo en
y tiempo en  )
)
a) ¿Cuál es la velocidad de la partícula?
El movimiento se efectúa en el plano xy; tenemos dos movimientos rectilíneos uniformes, de velocidades:
La velocidad de la partícula es:
La dirección esta dada por:
b) ¿Cuál es la trayectoria de la partícula?
Despejando t de una de las ecuaciones y remplazando en la otra obtenemos:
y=8t
 Si observamos ésta es la ecuación de una recta de la forma
Si observamos ésta es la ecuación de una recta de la forma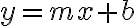 con pendiente
con pendiente  , y por tanto ésta es la ecuación que determina la trayectoria de dicha partícula.
, y por tanto ésta es la ecuación que determina la trayectoria de dicha partícula.
PREGUNTA: Sea un movimiento dado por  (distancia en m y tiempo en seg). ¿Cuál es la magnitud y dirección de la velocidad?. Recuerde que para calcula las componentes en los ejes coordenados, de la velocidad debe calcularlas teniendo en cuenta las pendientes de las rectas del movimiento que se describe.
(distancia en m y tiempo en seg). ¿Cuál es la magnitud y dirección de la velocidad?. Recuerde que para calcula las componentes en los ejes coordenados, de la velocidad debe calcularlas teniendo en cuenta las pendientes de las rectas del movimiento que se describe.
A) v=7,62m/seg
q=2,33º
B) v=58m/seg
q=2,33º
C) v=7,62m/seg
q=66,80º
D) v=58m/seg
q=0,040º
Movimiento circular
MOVIMIENTO CIRCULAR UNIFORME
Estudiaremos ahora un caso particular del movimiento en el espacio. Consideraremos un cuerpo moviéndose sobre un circulo de radio 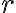 y deduciremos directamente la velocidad y la aceleración del cuerpo aplicando las definiciones vectoriales ya vistas.
y deduciremos directamente la velocidad y la aceleración del cuerpo aplicando las definiciones vectoriales ya vistas.
Para describir el movimiento rectilíneo de un cuerpo, se definió la posición, la velocidad y la aceleración del cuerpo y encontramos las ecuaciones cinemáticas del movimiento. De la misma manera, para describir el movimiento de rotación de un cuerpo, definiremos la posición angular y encontraremos las ecuaciones cinemáticas del movimiento circular.
Consideremos un cuerpo que se mueve sobre un círculo de radio 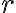 con rapidez constante, es decir, cuando la magnitud del vector velocidad es constante.
con rapidez constante, es decir, cuando la magnitud del vector velocidad es constante.
a) Velocidad
La velocidad o vector velocidad en un movimiento circular es tangente a la circunferencia (solo toca en un punto a la circunferencia sin que halla intersección entre el vector y la circunferencia) y perpendicular al radio que llega al punto de tangencia.
Además dicho vector velocidad varía en dirección más no en magnitud, es decir, va a a ser del mismo valor pero de diferente dirección.
Está determinada por:
Donde:
r es el radio de la circunferencia que circunscribe el movimiento
n el número de vueltas
Veamos un ejemplo:
¿Cuál es la velocidad media de una bicicleta que se mueve en linea recta, cuando sus ruedas de 40 cm de radio hacen 25 revoluciones por segundo?
Recordemos que una rps (revolución por minuto), significa 1 vuelta por segundo.
Siempre debemos expresar el tiempo en segundo
b) Aceleración normal o centrípeta:
En el movimiento circular uniforme, el módulo de la velocidad es constante; es decir, no varía. Sin embargo, en este tipo de movimientos sí existe una aceleración: la aceleración normal o centrípeta.
Esta aceleración es responsable de que la trayectoria del móvil sea una circunferencia. La aceleración centrípeta está siempre dirigida hacia el centro de la circunferencia.
Está determinada por:
Evidentemente, la dimensión de esta aceleración es en 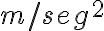 como se puede comprobar directamente.
como se puede comprobar directamente.
Ejemplo:
Una piedra gira en un circulo de radio 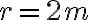 a razón de
a razón de  vueltas por segundo. ¿Cuál es su aceleración?
vueltas por segundo. ¿Cuál es su aceleración?
En un segundo, la piedra recorre una distancia igual a su rapidez.
Y la aceleración es:
Estática de la particula
Parte de la mecánica que analiza condiciones de equilibrio de un cuerpo, partícula o sistema de partículas, se basa en las leyes de la fuerza y del movimiento de Newton, o comúnmente conocidas como “Leyes de Newton”.
La experiencia muestra que si un cuerpo se pone en ciertas condiciones de interacción con otros cuerpos se pueden obtener:
a) El reposo o equilibrio con respecto a un sistema de referencia, es decir, la estática, del griego statikos (equilibrio).
b) El movimiento, es decir, la dinámica, del griego dynamis (fuerza).
Cantidades Básicas: Las cuatro cantidades siguientes se utilizan en el equilibrio:
Longitud: La longitud es necesaria para ubicar un punto en el espacio y de esta forma describir el tamaño de un sistema físico. Una vez que se define una unidad estándar de longitud, puede definirse cuantitativamente distancias y propiedades geométricas de un cuerpo como múltiplos de esa unidad de longitud.
Tiempo: El tiempo se concibe como una sucesión de eventos. Aunque los principios de la Estática son independientes del tiempo, esta cantidad definitivamente juega un papel importante en el estudio de la Dinámica.
Masa: La masa es una propiedad de la materia por la cual podemos comparar la acción de un cuerpo con la de otro. Esta propiedad se manifiesta como una atracción gravitacional entre dos cuerpos y proporciona una medida cuantitativa de la resistencia que presenta la materia al cambio de velocidad.
Fuerza: En general, la fuerza es considerada como un “jalón” o “tirón” ejercido por un cuerpo sobre otro. Esta interacción puede ocurrir cuando existe un contacto directo entre los cuerpos, por ejemplo, una persona empujando sobre una pared. Puede presentarse también a lo largo de una distancia determinada cuando los cuerpos se separan físicamente. Como ejemplos de este último caso están incluidas las fuerzas eléctricas, magnéticas y gravitacionales. En cualquier caso, una fuerza se caracteriza por su magnitud, dirección y punto de aplicación.
Partícula: Una partícula posee masa pero de tamaño poco significativo. Por ejemplo, el tamaño de la Tierra es insignificante comparado con el tamaño de su órbita, y por lo tanto la Tierra se puede tomar como una partícula cuando se estudia su movimiento orbital en un modelo. Cuando un cuerpo se idealiza como una partícula, los principios de la Mecánica se simplifican de manera importante, debido a que la geometría del cuerpo no se tomará en cuenta en el análisis del problema
Cuerpo Rígido: Un cuerpo rígido puede ser considerado como un conjunto formado por un gran número de partículas que permanecen separadas entre sí por una distancia fija antes y después de aplicar la carga. Como resultado, las propiedades del material de que está hecho cualquier cuerpo que se suponga rígido no se tendrá que considerar cuando se analicen las fuerzas que actúan sobre éste. En la mayoría de los casos, las deformaciones reales que se presentan en estructuras, máquinas, mecanismos, etcétera, son relativamente pequeñas, y la suposición de cuerpo rígido es apropiada para efectos de análisis.
Fuerza Concentrada: Una fuerza concentrada representa el efecto de una carga la cual se supone que actúa en algún punto de un cuerpo. Podemos representar este efecto por medio de una fuerza concentrada, siempre y cuando el área sobre la cual se aplica la carga sea relativamente pequeña comparada con el tamaño del cuerpo.
PREGUNTA: La estática de la partícula se refiere a:
TIPOS DE FUERZAS
Todas las interacciones que conocemos se traducen solamente por éstos tipos de fuerza:
Fuerzas gravitacionales
Es una fuerza de atracción entre dos cuerpos debido a que ambos poseen una cualidad que llamamos masa y que precisaremos más adelante.
Esta fuerza es muy débil, y para sentir su efecto es necesario que por lo menos uno de los dos cuerpos tenga una dimensión planetaria como el Sol, la Tierra, la Luna…..
Si abandonamos un cuerpo sobre la tierra, diremos que la fuerza gravitacional producida por la tierra sobre el cuerpo es el peso.
Fuerzas electromagnéticas
Se descompone en:
· Una fuerza eléctrica, que es la fuerza de atracción o de repulsión entre dos cuerpos debido a que ambos poseen una cualidad que llamamos carga eléctrica que precisaremos en electricidad.
· Una fuerza magnética, que es una fuerza adicional a la anterior cuando las cargas están en movimiento.
Estas fuerzas pueden ser también medidas por medio del resorte calibrado. Así, vemos que podemos calcular el valor de cualquier fuerza independientemente de su naturaleza, por la dirección y deformación de un resorte.
Fuerzas nucleares
Son fuerzas que aparecen cuando la distancia de los cuerpos es menor que  y desaparecen cuando esta distancia aumenta; se dice que son fuerzas de corto rango ya que origen exclusivamente en el interior de los núcleos atómicos.
y desaparecen cuando esta distancia aumenta; se dice que son fuerzas de corto rango ya que origen exclusivamente en el interior de los núcleos atómicos.
Estas fuerzas explican porque las partículas dentro del núcleo del átomo se mantienen unidas. Como no pueden medirse directamente, se piensa que el concepto de fuerza quizás no es muy adecuado para distancias tan pequeñas y que otros conceptos más complejos son necesarios.
Es interesante notar que estas diferentes fuerzas, cualquiera sea su naturaleza, se produce sin que haya contacto entre los cuerpos: por esta razón las denominamos fuerzas a distancia.
Actualmente, los físicos admiten que de cada cuerpo se “expande” algo abstracto que llamamos campo (campo gravitacional, campo electromagnético, campo nuclear) a la velocidad de la luz en el vació. Este campo al actuar sobre el otro cuerpo produce una fuerza. Efectivamente, si un cuerpo modifica su movimiento, la experiencia muestra que la fuerza que actuaba sobre otro cuerpo (debido al primer cuerpo) será modificado después de un tiempo igual a  , siendo
, siendo  la distancia de los dos cuerpos y c la velocidad de la luz. La teoría de la relatividad confirma este hecho.
la distancia de los dos cuerpos y c la velocidad de la luz. La teoría de la relatividad confirma este hecho.
Fuerzas de contacto
Llamaremos fuerza de contacto a la fuerza que un cuerpo hace a otro, debido sólo al contacto real entre los dos cuerpos.
Las fuerzas de contacto son realmente de naturaleza electromagnética y representan un número muy grande de interacciones entre los diferentes constituyentes de la materia. Como es imposible analizar estas interacciones una por una, se estudia su efecto global de manera empírica.
Estas fuerzas se denominan:
a) Fuerza elástica en el caso del resorte
b) Fuerza de tensión cuando uno de los cuerpos es una cuerda
c) Fuerza producida por la superficie de un cuerpo sobre la superficie en contacto de otro cuerpo. Esta fuerza en general se descompone en:
Una fuerza normal a las superficies en contacto
Una fuerza de rozamiento, paralela a las superficies en contacto.
PREGUNTA: La fuerza ejercida por la tierra par evitar que los objetos floten se denomina:
FUERZAS ELÁSTICAS
Fuerzas intermoleculares
Las Fuerzas Intermoleculares, son fuerzas de atracción y repulsión entre las moléculas. El comportamiento molecular depende en gran medida del equilibrio (o falta de él) de las fuerzas que unen o separan las moléculas.
Las fuerzas de atracción explican la cohesión de las moléculas en los estados liquido y sólido de la materia, y se llaman fuerzas de largo alcance o Fuerzas de Van der Waals en honor al físico holandés Johannes van der Waals. Estas fuerzas son las responsables de muchos fenómenos físicos y químicos como la adhesión, rozamiento, difusión, tensión superficial y la viscosidad.
Ley de Hooke
Cuando un objeto se somete a fuerzas externas, sufre cambios de tamaño o de forma, o de ambos. Esos cambios dependen del arreglo de los átomos y su enlace en el material.
Veamos la siguiente gráfica:
Muestra el aumento de longitud (alargamiento) de un alambre elástico a medida que aumenta la fuerza ejercida sobre el mismo. En la parte lineal de la gráfica, la longitud aumenta 10 mm por cada newton (N) adicional de fuerza aplicada. El cambio de longitud (deformación) es proporcional a la fuerza (tensión), una relación conocida como ley de Hooke. El alambre empieza a estirarse desproporcionadamente para una fuerza aplicada superior a 8 N, que es el límite de elasticidad del alambre. Cuando se supera este límite, el alambre reduce su longitud al dejar de aplicar la fuerza, pero ya no recupera su longitud original.
Tensión de una cuerda
Tomemos una cuerda fija en B y del otro extremo A halemos con una fuerza F
Como las moléculas de la cuerda se separaron, la fuerza de restitución, llamada tensión, se opondrá a la fuerza F. Notamos que en A, la tensión  está dirigida de A hacia B.
está dirigida de A hacia B.
En un punto cualquiera M de la cuerda, la parte MA produce una tensión 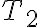 dirigida de M hacia
dirigida de M hacia 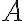 , y la otra parte
, y la otra parte 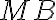 produce una tensión
produce una tensión 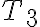 . En
. En 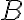 la tensión
la tensión 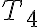 producida por todas las moléculas de la cuerda esta dirigida de B hacia A.
producida por todas las moléculas de la cuerda esta dirigida de B hacia A.
Fuerza Normal
Consideremos un cuerpo sobre una superficie plana, las moléculas comprimidas de la superficie producen sobre el cuerpo una fuerza elástica dirigida de la superficie hacia el cuerpo y normal a la superficie y que denominaremos fuerza normal.
Rozamiento
Consideremos de nuevo, un cuerpo sobre una superficie plana. Esta produce sobre el cuerpo una fuerza normal N.
Apliquemos al cuerpo una fuerza horizontal 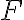 . Si esta fuerza es pequeña, el cuerpo no se mueve debido a que una fuerza
. Si esta fuerza es pequeña, el cuerpo no se mueve debido a que una fuerza  , que llamamos de rozamiento estático y producido por las fuerzas moleculares de la superficie sobre el cuerpo, la contrarresta. La experiencia muestra que esta fuerza crece hasta cierto límite proporcional a la fuerza normal o sea:
, que llamamos de rozamiento estático y producido por las fuerzas moleculares de la superficie sobre el cuerpo, la contrarresta. La experiencia muestra que esta fuerza crece hasta cierto límite proporcional a la fuerza normal o sea:
Denominaremos  el coeficiente estático de rozamiento.
el coeficiente estático de rozamiento.
Durante le movimiento, la fuerza de rozamiento, que llamamos ahora dinámica, opuesta la movimiento, se mantienen constante y proporcional a la fuerza normal, o sea
Siendo  el coeficiente dinámico de rozamiento.
el coeficiente dinámico de rozamiento.
Estas relaciones empíricas son aproximadamente independientes del área de contacto y de la velocidad del cuerpo.
Ejemplo 1:
Una superficie de coeficiente estático de rozamiento 0.3 y de coeficiente dinámico de rozamiento 0.2, produce sobren un cuerpo una fuerza normal de 20 Kg-f
· ¿Cuál es la fuerza de rozamiento estática máxima que puede actuar sobre el cuerpo?
· ¿Cuál es la fuerza de rozamiento dinámica que puede actuar sobre el cuerpo?
Ejemplo 2:
Un resorte tiene una fuerza de restitución de 30 Kg-f cuando se alarga 6 cm.
· ¿Cuál es la constante del resorte?
La variación en el resorte  es 6 cm
es 6 cm
· ¿Cuál es el alargamiento del resorte si la fuerza de restitución es 40 Kg-f?
· La fuerza de restitución anterior es igual a la fuerza de rozamiento dinámica que una superficie de coeficiente de rozamiento dinámico 0.5 produce sobre un cuerpo. ¿Cuál es la fuerza normal que la superficie produce sobre el cuerpo?
PREGUNTA: Un ejemplo típico de fuerza elástica se genera en:
Leyes de Newton
PRIMERA LEY DE NEWTON: LEY DE LA INERCIA
Cuando lanzamos un cuerpo sobre una mesa, el cuerpo se para después de alguna distancia. Si pulimos la mesa y el cuerpo, el cuerpo se desplazará mas lejos. Si ponemos un colchón de aire debajo del cuerpo, eliminamos prácticamente cualquier rozamiento, el cuerpo continúa su camino sin pararse aparentemente y la medida de su velocidad nos indica que es casi constante.
Entonces, podemos deducir que:
Todo cuerpo continúa en su estado de reposo o de movimiento rectilíneo uniforme, si no recibe ninguna interacción del exterior.
Esta ley implica que:
· Ninguna explicación es necesaria para justificarse la existencia de una velocidad.
· Para cambiar la dirección o la magnitud de la velocidad de un cuerpo, es decir para producir una aceleración,, se necesita una interacción del exterior del cuerpo.
Condiciones de equilibrio de una partícula
Según la primera Ley de Newton, una partícula esta en equilibrio o en movimiento rectilíneo uniforme si la suma de las fuerzas aplicadas sobre los ejes es igual a cero, o sea
Podemos dibujar un sistema de coordenadas cuyo origen sea la partícula y cuyos ejes tienen cualquier dirección y proyectar las fuerzas aplicadas sobre los ejes, entonces tenemos:
Si tenemos varias partículas de equilibrio o en movimiento rectilíneo uniforme, las ecuaciones de equilibrio se aplican para cada una de ellas.
Podemos ahora precisar la estabilidad del equilibrio.
Para un pequeño desplazamiento de la partícula en equilibrio:
a) la partícula regresa a su estado original, diremos que el equilibrio es estable. Por ejemplo, una esfera dentro de una semiesfera.
b) La partícula se aleja de su estado original, el equilibrio es inestable. Por ejemplo, una esfera encima de una semiesfera.
c) La partícula ni regresa ni se aleja de su estado original, el equilibrio es indiferente. Por ejemplo, una esfera sobre un plano.
SEGUNDA LEY DE NEWTON: LEY DE FUERZA
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza, nos dice que:
La fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que la relación se expresa:
F=ma
TERCERA LEY DE NEWTON:LEY DE ACCIÓN Y REACCIÓN
Si empujamos un objeto con la mano, la experiencia muestra que le objeto produce sobre la mano una fuerza igual pero opuesta.
Cuando halamos una cuerda, fijado sobre una pared, la tensión de la cuerda es la pared contrarrestada por una fuerza desarrollada por la pared.
Si un cuerpo es atraído por la Tierra (peso), también el cuerpo atrae hacia él a la Tierra. Situaciones análogas se presentan con las fuerzas electromagnéticas y nucleares.
De todos estos hechos experimentales, Newton dedujo la siguiente Ley:
Por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad y dirección, pero de sentido contrario sobre el cuerpo que la produjo.
En la figura se puede apreciar, que si un cuerpo A ejerce sobre el cuerpo B una fuerza  , el cuerpo B ejerce sobre A una fuerza
, el cuerpo B ejerce sobre A una fuerza  igual y opuesta.
igual y opuesta.
EJEMPLOS DE APLICACIÓN DE LAS LEYES DE NEWTON
Ejemplo 1:
Debido a la ley del equilibrio, las tensiones de una cuerda 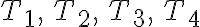 son iguales a F en magnitud. En el punto B, el muro necesariamente tendría que producir una fuerza resistente R igual a
son iguales a F en magnitud. En el punto B, el muro necesariamente tendría que producir una fuerza resistente R igual a 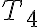 .
.
Notemos que la cuerda, en sus extremos, produce fuerzas de tracción  , es decir que la flecha que las representa está dirigida del extremo hacia el interior de la cuerda.
, es decir que la flecha que las representa está dirigida del extremo hacia el interior de la cuerda.
Ejemplo 2:
Un cuerpo de peso w, cuelga de una cuerda que en 0 está unida a otras dos cuerdas fijadas en el techo.
Se desea calcular las tensiones de las tres cuerdas sin peso.
Teniendo en cuenta las condiciones de equilibrio de la primera ley de Newton que indica que la suma de las fuerzas tanto en x como en y de un cuerpo en equilibrio debe ser 0, para el cuerpo tenemos:
Si consideramos el nudo como una partícula, las fuerzas aplicadas son: la tensión  que conocemos por la ecuación anterior,
que conocemos por la ecuación anterior, 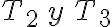
La ecuación del equilibrio nos da:
Proyectada sobre los ejes  y
y  las fuerzas y realizando lo cálculos en forma VECTORIAL (recuerda operaciones con vectores unidad 1) tenemos para el cuerpo o partícula:
las fuerzas y realizando lo cálculos en forma VECTORIAL (recuerda operaciones con vectores unidad 1) tenemos para el cuerpo o partícula:
O sea
La resolución de este sistema nos da:
Ejemplo 3:
Sobre un plano inclinado un ángulo  , sin rozamiento, se coloca un bloque de peso w. ¿Qué fuerza paralela al plano es necesaria para que el bloque se deslice a velocidad constante?
, sin rozamiento, se coloca un bloque de peso w. ¿Qué fuerza paralela al plano es necesaria para que el bloque se deslice a velocidad constante?
Notemos que la ecuación del equilibrio es valida, aunque el cuerpo este en reposo o suba o baje a velocidad constante.
Las fuerzas aplicas al bloque son:
a) El peso  que la tierra produce.
que la tierra produce.
b) La fuerza normal  que produce el plano.
que produce el plano.
c) La fuerza  que nosotros hacemos.
que nosotros hacemos.
Proyectemos sobre dos ejes, para este caso, paralela y perpendicularmente a plano ( a fin de simplificar las ecuaciones).
(Los dos ángulos de la figura son iguales porque sus lados son respectivamente perpendiculares)
Ejemplo 4:
El mismo problema pero ahora el plano es rugoso, con un coeficiente dinámico de rozamiento 
Aquí tenemos que especificar que el bloque sube a velocidad constante: la fuerza de rozamiento  será contraria al movimiento y se sumara a las fuerzas aplicadas anteriores.
será contraria al movimiento y se sumara a las fuerzas aplicadas anteriores.
Tendremos.
PREGUNTA: Se muestran 3 bloques de masas m1 = 2 kg. m2 = 3 kg. m3 = 8 kg. Si se supone nulo el roce, calcular la aceleración del sistema y las tensiones de las cuerdas.

A)a=0.8m/s2; T1=27.5N; T2=21.5N. B)a=1.4m/s2; T1=22.4N; T2=33.6N.
C)a=10m/s2; T1=21.5N; T2=27.5N. D) a=0.75m/s2; T1=21.1N; T2=27.1N.
Momento de fuerza o Torque
MOMENTO DE FUERZA
El momento de fuerza es necesario para poder analizar las condiciones que se deben cumplir para producir el equilibrio de un cuerpo rígido.
Para estudiar los movimientos de rotación de los cuerpos rígidos, es necesario introducir un nuevo concepto: momento de fuerza que une fuerza, dirección y distancia con respecto al eje de rotación.
Sea un cuerpo que puede girar solamente alrededor de un eje fijo 0 perpendicular al plano, el momento de fuerza o TORQUE es el producto de la fuerza (F) y la distancia (d) perpendicular entre la línea de acción de la fuerza y el punto de giro 0
Donde
M es el momento de fuerza o torque.
F es la fuerza aplicada
d es la distancia perpendicular entre la línea de acción de la fuerza y el punto de giro 0
Las unidades de momento son Fuerza por distancia = N*m (Newton*metro).
La convención del signo del momento de fuerza o torque será:
El momento de fuerza es positivo, si el efecto de la fuerza es producir una rotación alrededor de 0 contraria al movimiento de las agujas del reloj.
El momento de fuerza es negativo cuando la rotación se produce en el mismo sentido del movimiento de las agujas del reloj.
Si la dirección de la fuerza pasa por 0,es decir, si la fuerza se aplica en el punto de rotación 0 el movimiento de la fuerza es cero.
El momento es máximo cuando la fuerza es perpendicular a d.
EJERCICIO APLICATIVO:
Se tiene una barra de masa despreciable y 50 cm de longitud sujeta de un extremo (origen). A diferentes distancias del origen tenemos pesos de diferente masa colgando de la barra, tal como se muestra en la figura:
Calcular el momento de fuerza en el punto O y el valor de F para que la barra se encuentre en equilibrio.
Como se puede observar todos los pesos ejercen una fuerza hacia abajo de la barra por tanto el ángulo entre la barra y la dirección de la fuerza es de 90°.
M= [(10*10)+(50*20)+(25*20)+(50*25)+(10*35)+(25*50)]gr-f cm
M= 4450 gr-fcm
Si la barra no estuviera en equilibrio, es decir si no existiera F, la fuerza haría girar la barra al contrario de las manecillas del reloj, es decir, el momento sería positivo, tal como se calculó.
Como la barra se encuentra en equilibrio planteamos:
Para profundizar en éste tema ingresa al Vídeo momento de fuerza que encontrarás a continuación y en la dirección:
PREGUNTA: Para calcular el momento de fuerza de un cuerpo. se debe tener en cuenta:
* La distancia que existe entre el punto de aplicación de la
fuerza y el punto de corte de la recta perpendicular entre el punto de giro O y
la línea de acción de la fuerza.
* La distancia perpendicular que existe entre la línea de
acción de la fuerza y el punto de giro O.
* La distancia que existe entre el punto de aplicación de la
fuerza y el punto de giro O.
* La distancia vertical que existe entre el punto de
aplicación de la fuerza y el punto de giro O
Profundización Segunda ley de Newton: Dinámica
DINÁMICA DE LAS PARTICULAS
En cinemática, analizamos el movimiento de las partículas. En dinámica, estudiaremos como las interacciones producen el movimiento , y veremos que la segunda ley de newton es la ley fundamental de la dinámica.
Ley de la dinámica (Segunda ley de Newton)
La ley de la inercia indicaba que si no había fuerza sobre un cuerpo, este tenía un movimiento rectilíneo uniforme. Si ahora hacemos actuar una fuerza sobre un cuerpo, el cuerpo será acelerado
La experiencia muestra que la aceleración que experimenta es directamente proporcional a la fuerza y en la misma dirección, o sea que
El factor de proporcionalidad 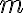 , denominado masa, es prácticamente constante si la velocidad del cuerpo es muy inferior a la velocidad de la luz y depende de la velocidad del cuerpo para los otros casos, como se demostrara en la Relatividad.
, denominado masa, es prácticamente constante si la velocidad del cuerpo es muy inferior a la velocidad de la luz y depende de la velocidad del cuerpo para los otros casos, como se demostrara en la Relatividad.
Como nuestra técnica actual no permite obtener para los cuerpos macroscópicos velocidades tan grandes, (pero si para los cuerpos macroscópicos) toda nuestra ingeniería descansa aun sobre la ley de la dinámica, con m constante.
Notemos que la primera ley de Newton es un caso particular de la segunda, en la cual a=0
Diferencia entre masa y peso
Cuando un cuerpo de masa 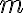 cae libremente, su aceleración es la de la gravedad
cae libremente, su aceleración es la de la gravedad  y la fuerza que actúa sobre él es su peso w. Por tanto, la segunda ley de Newton nos dice que el peso es
y la fuerza que actúa sobre él es su peso w. Por tanto, la segunda ley de Newton nos dice que el peso es  .
.
Es muy conveniente, en las diferentes aplicaciones que haremos, expresar el peso de un cuerpo por su valor mg.
Sistema de unidades
La segunda ley de la dinámica permite fijar la fuerza como magnitud derivada a partir de las magnitudes fundamentales de masa, longitud y tiempo. Su dimensión es:  .
.
En el sistema MKS (metro-Kilogramo-segundo), la unidad de fuerza será aquella que produce en una masa de 1 kilogramo una aceleración de  .
.
Esta unidad se llama 1 newton:
Solo utilizaremos este sistema por ser el de uso mas generalizado. A título de información damos rápidamente los otros sistemas que aún se utilizan.
En el sistema  (centímetro-gramo-segundo), la unida de fuerza (la DINA) será aquella que produce en una masa de un gramo de aceleración de un
(centímetro-gramo-segundo), la unida de fuerza (la DINA) será aquella que produce en una masa de un gramo de aceleración de un  , o sea
, o sea
En el sistema técnico se ha escogido como unidad fundamental la fuerza con su unidad de kilo-fuerza como hicimos en la lección anterior, y por tanto la masa es una unidad derivada. La unidad de masa (unidad técnica de masa o u.t.m.) será la de un cuerpo al cual una fuerza de un kg-f produce una aceleración de un 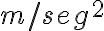 , o sea
, o sea
En el sistema técnico ingles, la fuerza es también la unidad fundamental. La unidad de masa (slug) será la de un cuerpo al cual una fuerza de una libra produce una aceleración de un  , o sea:
, o sea:
ECUACIONES DINAMICAS DEL MOVIMIENTO
La segunda ley de Newton, 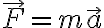 , es vectorial por lo tanto, si proyectamos sobre los ejes de coordenadas tenemos:
, es vectorial por lo tanto, si proyectamos sobre los ejes de coordenadas tenemos:
Que denominamos las ecuaciones dinámicas del movimiento. Si se conoce la masa del cuerpo, se deducen las diferentes aceleraciones y de aquí las ecuaciones cinemáticas del movimiento.
Para el caso particular del movimiento circular uniforme, como sabemos que la aceleración es centrípeta y vale  , la fuerza resultante que actúa sobre el cuerpo es también centrípeta y vale
, la fuerza resultante que actúa sobre el cuerpo es también centrípeta y vale
Esto nos permitirá conocer la velocidad del cuerpo.
REGLAS BÁSICAS DE RESOLUCIÓN DE PROBLEMAS DE DINÁMICA
1. Dibujar un esquema general del problema.
2. Para cada cuerpo de estudio, se construye el diagrama vectorial de todas las fuerzas que actúan sobre el cuerpo sin olvidar el peso mg y las fuerzas aun desconocidas. Cada fuerza se representa por un vector cuyo origen parte del cuerpo considerado como un punto.
3. Se escoge un sistema de coordenadas perpendiculares para cada cuerpo, cada eje en la dirección de la aceleración correspondiente y se calculan los componentes de las fuerzas. Frecuentemente, como las fuerzas son coplanarias, 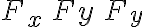 serán suficientes.
serán suficientes.
4. Para cada eje de coordenada se escribe la segunda ley de newton y se resuelven las ecuaciones, para responder las preguntas formuladas. (Consideraremos las cuerdas y las poleas con masa despreciable y tomaremos  ).
).
APLICACIÓN DE LAS REGLAS BÁSICAS DE RESOLUCIÓN DE PROBLEMAS DE DINÁMICA UTILIZANDO LAS LEYES DE NEWTON
Una bolsa de cemento de 325 Newton de peso cuelgan de 3 alambres como muestra la figura. Dos de los alambres forman ángulos:
θ1 = 600 θ2 = 250 con la horizontal.
Si el sistema esta en equilibrio encuentre las tensiones T1 , T2 y T3
Solucionamos el sistema de ecuaciones lineales (2 ecuaciones 2 incógnitas) Remplazamos 1 en 2
EJEMPLOS DE APLICACIÓN
Ejemplo 1:Apliquemos una fuerza de 30 newtons paralela al eje x y una fuerza de 40 newtons paralela al eje y a un cuerpo de masa 10 kg. ¿Cuál es la aceleración resultante?
La segunda ley nos da:
La magnitud de la aceleración resultante es
Y la dirección que hace con la horizontal se obtiene por:
Ejemplo 2:Un ascensor de masa  tiene una aceleración hacia arriba de
tiene una aceleración hacia arriba de  . ¿Cuál es la tensión del cable que lo mueve?
. ¿Cuál es la tensión del cable que lo mueve?
La segunda ley nos da:
Notemos que la tensión del cable es mayor que el peso del ascensor. (Una aceleración hacia arriba indica que el ascensor esta subiendo acelerándose o que baja frenándose).
Ejemplo 3:¿Cuál es el peso aparente de una persona de 80 kg dentro del mismo ascensor con la misma aceleración?
Llamaremos peso aparente a la fuerza normal N que hace el suelo de una balanza sobre la persona.
Tenemos
Ejemplo 4:Un bloque de 10 kg se mueve sobre un plano horizontal y esta unido por un hilo a un segundo bloque de 40kg. ¿cuál es la aceleración de los bloques y la tensión del hilo:
a) Cuando no hay rozamiento.
Para cada cuerpo, dibujamos las fuerzas aplicadas a él, sin olvidar la fuerza normal que produce le plano, y por la segunda ley con respecto a los ejes representados, tenemos:
Cuerpo A
En la dirección  denominaremos
denominaremos  la aceleración y en la dirección
la aceleración y en la dirección  , como el cuerpo conserva siempre la misma ordenada, la aceleración es 0.
, como el cuerpo conserva siempre la misma ordenada, la aceleración es 0.
Cuerpo B
El eje y para este problema fue escogido hacia abajo, es decir en la dirección de la aceleración que en este caso es a, la misma que parea el cuerpo A debido a que el hilo no es elástico y por lo tanto cada cuerpo recorre distancias iguales en el mismo tiempo.
Reuniendo las tres ecuaciones numéricamente tenemos:
La resolución del sistema nos da
b) Hay rozamiento y el coeficiente de rozamiento es 0.2.
Debemos agregar la fuerza de rozamiento  contraria al movimiento (figura b). La segunda ley nos da:
contraria al movimiento (figura b). La segunda ley nos da:
La resolución numérica nos da: 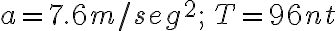 .
.
Ejemplo 5:Un bloque sin velocidad inicial se desliza sobre un plano inclinado de  . Después de 3 segundos qué distancia recorre.
. Después de 3 segundos qué distancia recorre.
a) si no hay rozamiento.
El peso se descompone en las dos componentes como se ve en la figura c, y por la segunda ley tenemos:
Los ángulos marcados  en la figura son iguales debido a que tienen los lados respectivamente perpendiculares y que son ángulos agudos.
en la figura son iguales debido a que tienen los lados respectivamente perpendiculares y que son ángulos agudos.
Numéricamente tenemos:
Como la aceleración es constante, tenemos un movimiento uniformemente acelerado, o sea:
b) Si hay rozamiento entre las dos superficies y el coeficiente de rozamiento es 0.2.
Agregamos la fuerza de rozamiento 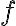 contraria al movimiento (figura d) y por la segunda ley tenemos:
contraria al movimiento (figura d) y por la segunda ley tenemos:
La resolución de este sistema de ecuaciones nos da:
Y la distancia recorrida es:
PREGUNTA: Apliquemos una fuerza de 30 newtons a un cuerpo de masa 10 kg. ¿cuál es la aceleración resultante?
A) a=3 m/seg2
B) a=0.3 m/seg2 C) a=3
cm/seg2 D) a=30 m/seg2
Trabajo
Se realiza trabajo cuando una fuerza mueve un cuerpo en la dirección en que ella actúa.
El trabajo denominado por la letra  es el producto de la fuerza por el desplazamiento por el coseno del ángulo formado entre la fuerza (F) y el desplazamiento (
es el producto de la fuerza por el desplazamiento por el coseno del ángulo formado entre la fuerza (F) y el desplazamiento ( )
)
Bajo la acción de la fuerza 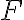 , el cuerpo se desplaza una distancia
, el cuerpo se desplaza una distancia  . Por definición, el trabajo realizado por
. Por definición, el trabajo realizado por 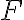 es:
es:
Unidades
En el Sistema Internacional de Medidas, la unidad del trabajo es el Joule y se calcula como:
1 Joule = 1 Newton x 1 Metro
Trabajo nulo
Para que haya trabajo debe haber desplazamiento. Hay fuerzas que no realizan trabajo.
Por ejemplo, en el desplazamiento de un cuerpo sobre una superficie, la normal no realiza trabajo ya que el coseno del ángulo entre los vectores fuerza y desplazamiento vale cero.
La fuerza "peso" no realiza trabajo en un desplazamiento horizontal. En cambio, si el cuerpo sube y baja volviendo al mismo lugar hay un trabajo positivo y otro negativo, por lo que tampoco se realiza trabajo volviendo al mismo punto.
El trabajo vale cero si
El Desplazamiento = 0
Cos θ = 0
F = 0
Ejemplo 1:
¿Cuál es el trabajo de una fuerza constante de  paralela al eje
paralela al eje  y que se desplaza
y que se desplaza  ?
?
Si el trabajo es positivo, se denomina motor.
Ejemplo 2:
Se considera una fuerza  paralela al eje x como muestra la figura, aplicada a un cuerpo. Este, bajo la acción de otras fuerzas (no representadas en la figura), se desplaza una distancia de
paralela al eje x como muestra la figura, aplicada a un cuerpo. Este, bajo la acción de otras fuerzas (no representadas en la figura), se desplaza una distancia de  en sentido contrario a la fuerza F. ¿Cuál es el trabajo realizado por F?
en sentido contrario a la fuerza F. ¿Cuál es el trabajo realizado por F?
Aquí, el ángulo 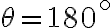 y como
y como 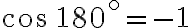 tenemos:
tenemos:
Si el trabajo es negativo se dirá que el trabajo es resistente.
Ejemplo 3:
¿Cuál es el trabajo que realiza una fuerza centrípeta cuando el cuerpo describe un círculo?
No hay trabajo porque la fuerza centrípeta es a cada instante perpendicular a su desplazamiento.
NOTA: Cuando una persona cargada con un cuerpo se traslada horizontalmente, la persona tiene que hacer una fuerza  hacia arriba para contrarrestar el peso del cuerpo, pero no realiza ningún trabajo a pesar de que pueda sentirse fatigada, porque el desplazamiento es perpendicular a N.
hacia arriba para contrarrestar el peso del cuerpo, pero no realiza ningún trabajo a pesar de que pueda sentirse fatigada, porque el desplazamiento es perpendicular a N.
Si un hombre sostiene un objeto en reposo o empuja un cuerpo sin moverlo, no realiza ningún trabajo porque no hay desplazamiento, aunque sienta cansancio debido a la tensión que hay en sus músculos.
Estos ejemplos nos muestran la importancia de no confundir nuestras nociones subjetivas de fatiga o esfuerzo con el significado muy diferente que se hace en física de la palabra trabajo.
Rendimiento
La noción de rendimiento se asocia a la de trabajo. Se define como el trabajo realizado por una máquina (trabajo útil) w dividido por el trabajo comunicado a la máquina w, o sea:
Este rendimiento es siempre menor que 1 debido a que parte del trabajo comunicado a la máquina se trasforma en trabajo no útil. (trabajo de las fuerzas de rozamiento...)
Ejemplo 4:
Por medio de poleas, una fuerza de  levanta un peso de
levanta un peso de  . Cuando la fuerza se desplaza en su dirección,
. Cuando la fuerza se desplaza en su dirección,  , el peso sube
, el peso sube 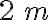 . ¿Cuál es el rendimiento de las poleas?
. ¿Cuál es el rendimiento de las poleas?
Solución:
Mientras que el trabajo útil realizado por las poleas es .
El rendimiento de las poleas es por tanto,
PREGUNTA: Se considera una fuerza F de  que forma con el eje
que forma con el eje  un ángulo de
un ángulo de  , y se desplaza una distancia de 8 m. ¿Cuál es el trabajo realizado por
, y se desplaza una distancia de 8 m. ¿Cuál es el trabajo realizado por 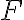 ?
?
A) -30 JULIOS B) -32JULIOS C) 32JULIOS D) 30JULIOS
POTENCIA
Cuando se definió el concepto de trabajo no se hizo referencia al tiempo invertido para realizarlo. Es muy conveniente para poder comparar diferentes máquinas, saber qué cantidad de trabajo se efectúa en la unidad de tiempo. Por esto se define:
Potencia media
Es el trabajo realizado dividido por el tiempo trascurrido. Se denomina potencia por la letra  .
.
Si el deplazamiento es horizontal se tiene que la potencia es:
Donde:
F es la fuerza aplicada
x es el desplazamiento
 es el ángulo entre la fuerza y el desplazamiento.
es el ángulo entre la fuerza y el desplazamiento.
Cuando el desplazamiento es vertical podemos decir que la fuerza que actúa sobre el cuerpo es de igual magnitud a su peso F=Peso=m*g y que la distancia recorrida será la altura (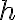 )a la cual se desplazó.
)a la cual se desplazó.
Si el desplazamiento es vertical se tiene que la potencia es:
Donde:
m es la masa
h es la altura o desplazamiento en vertical del cuerpo
Unidades:
En el sistema internacional las unidades de la potencia son 
También se puede expresar como 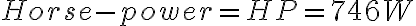
 realizando la respectiva conversión.
realizando la respectiva conversión.
Relación entre potencia y velocidad
De la definición de potencia y velocidad se puede deducir:
Donde  es el ángulo formado entre la fuerza (F) y el desplazamiento (
es el ángulo formado entre la fuerza (F) y el desplazamiento ( ).
).
Si el desplazamiento es horizontal, significa que el ángulo  es cero, es decir,
es cero, es decir, 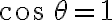
Por tanto la fuerza ejercida será:
Ejemplo:
Un motor levanta a velocidad constante un cuerpo de 100 kg a una altura de 20 m en un tiempo de 5 segundos. ¿Cuál es la potencia del motor?
(El motor produce una fuerza 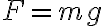 debido a que el cuerpo se levanta a velocidad constante).Su potencia será:
debido a que el cuerpo se levanta a velocidad constante).Su potencia será:
Recordemos que para efectos de cálculo podemos utilizar el valor de la gravedad como 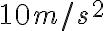 , pero sin olvidar que el valor real es
, pero sin olvidar que el valor real es 
Que se puede escribir también
PREGUNTA: Una locomotora de  arrastra unos vagones con velocidad de
arrastra unos vagones con velocidad de  . ¿Cuál es la fuerza de tracción ejercida por la locomotora?
. ¿Cuál es la fuerza de tracción ejercida por la locomotora?
A)100
newtons B)100.000 newtons C)10.000 newtons D)1.000 newtons
Energía
La energía se define como la capacidad de producir trabajo, por lo tanto también se mide en Joules. Un Joule de energía puede producir un Joule de trabajo. Existen distintos tipos de energía tales como la eléctrica, nuclear, química, mecánica, etc.
Energía cinética (Ec)
Es la energía que tiene un cuerpo debido a su velocidad. Sin embargo, la energía que transfiere el cuerpo no depende solamente de su velocidad. Es bastante obvio que un camión que circula a 40 km/h produce más daño en una pared que una bicicleta que circule a la misma velocidad. Así, la energía cinética depende de la masa del cuerpo.
Se calcula como:
Ejemplo:
Una fuerza de  arrastra un objeto de masa de
arrastra un objeto de masa de  , inicialmente en reposo, una distancia de
, inicialmente en reposo, una distancia de 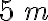
a) ¿Cuál es el trabajo de la fuerza?
b) ¿Cuál es la energía cinética del objeto?
Calculamos la velocidad del objeto, teniendo en cuenta las ecuaciones cinemáticas vistas en la unidad 2:
Ahora por la segunda ley de Newton tenemos que  , despejando
, despejando  obtenemos:
obtenemos:
Ahora reemplazamos en la ecuación de energía cinética:
Por definición la energía es la capacidad de producir trabajo, y ésto queda comprobado observando el valor de
y comparándolo con el valor de
encontrado.
Energía Potencial (Ep)
La energía potencial es aquella que tiene un cuerpo debido a su posición en un determinado momento. Por ejemplo un cuerpo que se encuentra a una cierta altura puede caer y provocar un trabajo o un resorte comprimido o estirado puede mover un cuerpo también produciendo trabajo.
Existen dos clases de energía potencial:
Energía potencial gravitacional Epg (cerca de la tierra)
Es la que tienen los cuerpos debido a la gravedad de la tierra. Se calcula multiplicando el peso por la altura.
Se suele considerar que a una altura cero la Epg es cero, por lo tanto se calcula como:
Donde:
h = Altura
m = Masa
g = Aceleración de la gravedad ( )
)
Energía potencial elástica (Epe)
Es la energía acumulada en un cuerpo elástico tal como un resorte.
Se calcula como:
K = Constante del resorte
x = Desplazamiento desde la posición normal
Epe = Energía potencial elástica
PREGUNTA: ¿Qué energía potencial posee un cuerpo de masa 5 kg colocado a 2 m del suelo?. (Gravedad=g= )
)
A)88J B) 11J C) 10J D) 98J
Conservación de la energía mecánicaEnergía mecánica (Em)
La energía mecánica es la suma de la energía potencial y la energía cinética de un cuerpo. A su vez la energía potencial suele considerarse formada por la suma de la energía potencial gravitatoria y potencial elástica. Por lo tanto la energía mecánica la podemos definir como:
 = Energía mecánica
= Energía mecánica = Energía potencial
= Energía potencial = Energía cinética
= Energía cinética = Energía potencial gravitatoria
= Energía potencial gravitatoria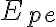 = Energía potencial elástica
= Energía potencial elástica
PREGUNTA: ¿Qué energía mecánica posee un cuerpo de 20 g, que oscila atado a un resorte de constante 20 N/m. Si la velocidad en la posición de equilibrio es de 4 m/s y no se considera fricción. NOTA: en la posición de equilibrio la Ep=0, es decir, Em=Ec.
A) 0.16N B) 1.6J C) 160J D) 0.16J
SITIO WEB ENERGIA CINETICA
http://www.acienciasgalilei.com/videos/gravitacion.htm
PROBLEMAS RELACIONADOS CON ENERGÍA
Caída libre
Muchos problemas de caída libre (con  constante) pueden resolverse inmediatamente por conservación de la energía.
constante) pueden resolverse inmediatamente por conservación de la energía.
Por ejemplo:
¿Cuál será la velocidad de un cuerpo que cae de una 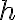 sin velocidad inicial?
sin velocidad inicial?
En este caso la energía potencial con respecto al suelo se trasforma integralmente en energía cinética, o sea
Si el cuerpo se lanza con una velocidad inicial  en cualquier dirección, su velocidad
en cualquier dirección, su velocidad 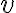 al llegar al suelo estará dada por:
al llegar al suelo estará dada por:
En particular si un cuerpo se lanza del suelo con velocidad  , ¿Con qué velocidad regresa el suelo?.
, ¿Con qué velocidad regresa el suelo?.
Inicialmente el cuerpo solamente tiene energía cinética (la energía potencial es 0 con respecto al suelo). Durante el movimiento, se trasforma en energía potencial y durante el regreso se convierte en energía cinética con velocidad  , o sea, finalmente,
, o sea, finalmente,
Obsérvese en consecuencia que la magnitud de 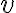 es igual a la magnitud de
es igual a la magnitud de  pero la conservación de la energía mecánica no nos da la dirección de la velocidad.
pero la conservación de la energía mecánica no nos da la dirección de la velocidad.
Péndulo
El péndulo es un ejemplo sencillo de la conservación de la energía mecánica si se admite que no hay rozamiento.
Inicialmente, la energía potencial con respecto a un plano horizontal que pasa por la posición de equilibrio del péndulo se trasforma paso por paso en energía cinética siguiendo la ecuación.
Hasta trasformarse completamente, en el punto de equilibrio, en energía cinética,
Inmediatamente empieza el proceso inverso; esta energía cinética poco a poco en energía potencial.
Resorte
Es un ejemplo de trasformación de energía potencial elástica en energía cinética y viceversa.
Sea un cuerpo de masa 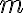 en el extremo de un resorte sobre una mesa horizontal sin rozamiento. Si alargamos el resorte en una distancia
en el extremo de un resorte sobre una mesa horizontal sin rozamiento. Si alargamos el resorte en una distancia  y lo soltamos, la energía potencial elástica del resorte se trasforma completamente en energía cinética cuando el cuerpo pasa por la posición de equilibrio, o sea
y lo soltamos, la energía potencial elástica del resorte se trasforma completamente en energía cinética cuando el cuerpo pasa por la posición de equilibrio, o sea
Este efecto se utilizó en las antiguas armas como los arcos, arbaletas, catapultas,... algunos juguetes y relojes.
Plano inclinado
Sobre un plano inclinado sin rozamiento, un cuerpo de masa 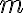 se desliza sin velocidad inicial de una altura
se desliza sin velocidad inicial de una altura 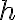 . ¿Cuál es su velocidad
. ¿Cuál es su velocidad 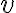 al final del recorrido?
al final del recorrido?
Por conservación de la energía, tenemos
(Este caso se generaliza a cualquier superficie, siempre que no haya rozamiento).
Ahora el plano inclinado tiene un coeficiente de rozamiento  . ¿Cuál será la velocidad
. ¿Cuál será la velocidad  al final del recorrido.
al final del recorrido.
Parte de su energía potencial gravitacional se convierte en calor debido al trabajo de la fuerza de rozamiento y parte se convierte en energía cinética; tenemos:
Por tanto
PREGUNTA: Un ejemplo de trasformación de energía potencial elástica en energía cinética y viceversa es?
Impulso y cantidad de movimiento
IMPULSO
El impulso (I) es el producto entre la fuerza y el tiempo durante el cual está aplicada dicha fuerza en el cuerpo. Si la fuerza es constante el impulso se calcula multiplicando la F por Δt.
Recuerda que Δt significa variación en el tiempo ya que Δ es cambio o variación.
CANTIDAD DE MOVIMIENTO
La cantidad de movimiento (p) es el producto de la velocidad por la masa. La velocidad es un vector mientras que la masa es un escalar. Como resultado obtenemos un vector con la misma dirección y sentido que la velocidad.
La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
RELACIÓN ENTRE IMPULSO Y CANTIDAD DE MOVIMIENTO
El impulso aplicado a un cuerpo es igual a la variación de la cantidad de movimiento, por lo cual el impulso también puede calcularse como:
Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de su masa:
En el caso particular de una fuerza constante o de una fuerza media  , y para un intervalo
, y para un intervalo  (tiempo final - tiempo inicial), tendremos:
(tiempo final - tiempo inicial), tendremos:
Por tanto tendríamos:
Ejemplo:
Una esfera de masa  con velocidad
con velocidad 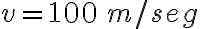 choca contra una pared y rebota con igual rapidez pero en sentido contrario. El choque duró
choca contra una pared y rebota con igual rapidez pero en sentido contrario. El choque duró  segundos. Calcular la fuerza media ejercida por la pared sobre la esfera.
segundos. Calcular la fuerza media ejercida por la pared sobre la esfera.
Primero realizamos un dibujo de lo que nos plantea el problema:
Como el choque va dirigido en sentido del eje x negativo decimos que  es negativa.
es negativa.
Al rebotar la bola se dirige hacia el sentido positivo de x por tanto  es positiva.
es positiva.
El problema nos indica el tiempo que duró el choque, por tanto decimos que  seg
seg
Ahora despejamos la fuerza media que nos indica el problema:
Recordemos que las unidades que debemos trabajar siempre son: masa en Kg, velocidad en m/s y tiempo en segundos. Así que siempre que sea necesario se debe realizar conversión de unidades para trabajar en la forma descrita anteriormente.
PREGUNTA: El momento lineal o cantidad de movimiento de una partícula está dado por:
Conservación de la cantidad de movimiento
La ley de conservación de la cantidad de movimiento señala que si sobre un sistema de partículas no actúan fuerzas externas o la suma de las fuerzas externas es nula, entonces la cantidad de movimiento total del sistema es constante.
Consideremos dos cuerpos de masa  y
y  , aislados del exterior, con velocidades iniciales
, aislados del exterior, con velocidades iniciales  y
y  antes que interactúen
antes que interactúen
entre ellos, con velocidades finales  y
y  después de la interacción.
después de la interacción.
Durante la interacción, el cuerpo 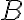 ejerce sobre el cuerpo
ejerce sobre el cuerpo 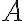 la fuerza
la fuerza  mientras que le cuerpo
mientras que le cuerpo 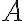 ejerce sobre
ejerce sobre 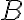 la fuerza
la fuerza  (No hay fuerza del exterior de los cuerpos).
(No hay fuerza del exterior de los cuerpos).
Para el cuerpo 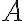 , por el teorema anterior, se tiene
, por el teorema anterior, se tiene
Las fuerzas  y
y  forman una pareja de fuerzas de acción y reacción y por la tercera ley de Newton
forman una pareja de fuerzas de acción y reacción y por la tercera ley de Newton
Y por tanto
O sea
Finalmente obtenemos la ecuación que nos describe la conservación de la cantidad de movimiento:
La cantidad de movimiento total de los cuerpos antes de la interacción es igual a la cantidad de movimiento total después de la interacción cuando no actúan fuerzas externas a los cuerpos.
Como es una ley vectorial, si se tiene una interacción en el plano, proyectando los vectores cantidades de movimiento sobre los ejes, se tienen dos ecuaciones de las componentes.
Es de notar que durante la interacción, las fuerzas que se producen pueden ser muy grandes, especialmente en las colisiones, y por tanto, frecuentemente se puede despreciar las fuerzas externas y aplicar la conservación de la cantidad de movimiento.
Ejemplo 1:
Un bloque de 5 kg con velocidad de 20 m/seg choca con otro bloque de 2 kg con velocidad de 15 m/seg dirigida en sentido contrario.
Si se admite que después del choque quedan unidos, ¿Cuál será la velocidad del conjunto?.
Si tomamos en el eje  como muestra la figura, una velocidad es positiva, mientras que la otra es negativa.
como muestra la figura, una velocidad es positiva, mientras que la otra es negativa.
Aplicando la conservación de la cantidad de movimiento, tenemos
Como este resultado es positivo, la velocidad del conjunto es  en la dirección del eje
en la dirección del eje  .
.
Ejemplo 2:
Se dispara una bala de 20 g con velocidad de 500 m/seg con un fusil de 5 kg. ¿Cuál es la velocidad de retroceso del fusil?
El conjunto bala-fusil está inicialmente en reposo y por tanto, su cantidad de movimiento es 0. Después de la interacción (explosión) la bala y el fusil tienen cada uno una cantidad de movimiento que satisface la ecuación.
La velocidad del fusil es contraria a la de la bala,
PREGUNTA: Un bloque de masa m1 = 1,6 kg. Que se mueve inicialmente hacia la derecha con una velocidad de 4 m/seg. Sobre una pista horizontal sin fricción choca con un resorte unido a un segundo bloque de masa m2 = 2,1 kg. Que se mueve hacia la izquierda con una velocidad de 2,5 m/seg. Como muestra la figura. El resorte tiene una constante de resorte de 600 N/m. En el instante en el que m1 se mueve hacia la derecha con una velocidad de 3 m/seg, determine la velocidad de m2:

A) -3M B) 3M C) -1.738M D) 1.738M
Fenómenos de colisiones
FENÓMENOS DE COLISIONES
En los fenómenos de colisiones o choques podemos aplicar la ley de la conservación de movimiento.
CHOQUES ELÁSTICOS
Es aquella colisión en la cual la energía cinética total y la cantidad de movimiento del sistema son iguales antes y después del choque.
Este tipo de choque se presenta cuando dos partículas de masas  y
y  se mueve con velocidades iniciales
se mueve con velocidades iniciales 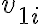 y
y  a lo largo de la misma recta. Las dos partículas chocan de frente y se alejan la una de la otra con velocidades finales
a lo largo de la misma recta. Las dos partículas chocan de frente y se alejan la una de la otra con velocidades finales  y
y  .
.
Este tipo de choques se pueden definir con la ecuación de conservación de cantidad de movimiento en choques elásticos:
Si cancelamos 1/2 de la ecuación obtenemos:
También podemos utilizar la relación de velocidad expresada como:
Ejemplo 1:
Un deslizador de 0.150 Kg se mueve a la derecha con una velocidad de 0.80  , en un riel de aire horizontal sin fricción. Se encuentra de frente con otro deslizador de 0.300 Kg que se mueve hacia la izquierda a 2.20
, en un riel de aire horizontal sin fricción. Se encuentra de frente con otro deslizador de 0.300 Kg que se mueve hacia la izquierda a 2.20  . ¿Cuál es la velocidad final (magnitud y dirección)de cada deslizador si el choque es elástico?
. ¿Cuál es la velocidad final (magnitud y dirección)de cada deslizador si el choque es elástico?
Primero realizamos un dibujo en donde se pueda ver lo que nos plantea el ejercicio y los signos que toma cada variable dependiendo hacia el lado del eje x que se dirija:
X
Ahora planteamos nuestra ecuación de choques elásticos:
Y reemplazamos los valores que conocemos:
Ahora con la relación de velocidad tenemos:
Tenemos entonces un sistema de dos ecuaciones y dos incógnitas: Si no recuerdas como se soluciona ingresa a matemáticas grado 9 unidad 3.
PRIMERO ORDENAMOS LAS ECUACIONES PARA QUE LAS VARIABLES ESTÉN EN EL MISMO ORDEN:
Multiplicamos la ECUACIÓN 2 por (-0.300) y la sumamos con la ECUACIÓN 1:
+
=
ESTA ES LA VELOCIDAD FINAL DEL PRIMER DESLIZADOR, EL SIGNO NOS INDICA QUE SE DIRIGE HACIA LA IZQUIERDA.
Ahora reemplazamos en cualquiera de las ecuaciones éste valor para determinar la velocidad final del segundo deslizador:
ESTA ES LA VELOCIDAD FINAL DEL SEGUNDO DESLIZADOR, EL SIGNO NOS INDICA QUE SE DIRIGE HACIA LA IZQUIERDA.
CHOQUES TOTALMENTE INELÁSTICOS
En el choque totalmente inelástico los bloques quedan pegados después de la colisión. Si sobre dichos cuerpos no actúan las fuerzas de fricción, entonces se conserva la cantidad de movimiento, la cual tiene la siguiente expresión:
Es necesario observar que la suma de la energía cinética de cada uno de los bloques no es igual a la energía cinética del conjunto después de la colisión.
Este tipo de choque se presenta cuando dos partículas de masas  y
y  se mueve con velocidades iniciales
se mueve con velocidades iniciales 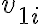 y
y  a lo largo de la misma recta. Las dos partículas chocan de frente y se alejan la una de la otra con la misma velocidad
a lo largo de la misma recta. Las dos partículas chocan de frente y se alejan la una de la otra con la misma velocidad  ya que ahora forman un conjunto en movimiento.
ya que ahora forman un conjunto en movimiento.
Debido a que la cantidad de movimiento de un sistema aislado se conserva en cualquier choque, podemos decir que la cantidad total de movimiento antes de la colisión es igual a la cantidad total de movimiento del sistema combinado después del choque.
Este tipo de choques se puede definir con la ecuación de conservación de cantidad de movimiento en choques inelásticos:
Ejemplo 2:
Dos patinadores en una pista de hielo sin fricción chocan y quedan agarrados. Uno de ellos tiene una masa de 70 Kg y se dirige hacia la derecha con una velocidad de 2 , mientras que el otro tiene una masa de 65 Kg y se dirigía hacia la izquierda con velocidad de 2.5
, mientras que el otro tiene una masa de 65 Kg y se dirigía hacia la izquierda con velocidad de 2.5 . ¿Cuál es la velocidad (magnitud y dirección) de los patinadores inmediatamente después del choque?
. ¿Cuál es la velocidad (magnitud y dirección) de los patinadores inmediatamente después del choque?
Recordemos siempre realizar una gráfica donde se plasme lo que indica el ejercicio:
Ahora remplazamos los valores conocidos en la ecuación de choques inelásticos:
ESTA ES LA VELOCIDAD DEL CONJUNTO, EL SIGNO INDICA QUE SE DIRIGE HACIA LA IZQUIERDA.
Ahora veamos otro ejemplos para complementar el tema:
Ejemplo 3:
Un bloque A de masa 2 kg parte del reposo de una altura 5 m como muestra la figura. Choca de una manera inelástica con el bloque B de igual masa y el conjunto comprime el resorte de constante 250 nt/m. ¿Cuál fue la distancia de compresión del resorte si no hay rozamiento en ninguna parte de la superficie?
Este problema se divide en tres partes:
Primero: Calculemos la velocidad que A tendrá en el momento del choque contra B. Por la conservación de la energía tenemos:
Segundo: Calculemos la velocidad 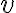 del conjunto después del choque. Por la conservación de la cantidad de movimiento tenemos,
del conjunto después del choque. Por la conservación de la cantidad de movimiento tenemos,
Tercero: Calculemos la compresión del resorte. Por la conservación de la energía tenemos,
PREGUNTA: Un carro de tren de 30 kg se mueve hacia la derecha a una velocidad de 25 m/s. Este colisiona con otro vagón estacionado que tiene un peso de 50 kg. Los carros quedan unidos y siguen andando a lo largo de las vías.
¿Cuál es la velocidad después de la colisión?

A) -15.6m/s:5.625m/s. B) 5.625m/s. C) 9.375m/s. D) -15.6m/s.
VIDEO DE COLISIONES
Hidrostática
La hidrostática es el estudio de los fluidos en reposo y las fuerzas y presiones que los afectan.
FLUIDO: Se refiere a la materia que puede fluir, pudiendo trasladar su masa desde una zona de mayor presión a otra de menor presión y que puede cambiar de forma debido a la acción de pequeñas fuerzas. Los fluidos poseen partículas cuyas fuerzas de atracción (fuerzas de cohesión) no son lo suficientemente potentes para mantener su masa en una forma definida. Existen tres tipos de fluidos: LÍQUIDOS GASES Y PLASMAS.
Los gases carecen de fuerzas de cohesión y los líquidos poseen fuerzas de cohesión muy débiles, lo que permite separar de manera sencilla a pequeñas porciones de materia.
Definiciones básicas:
Densidad de un líquido: La densidad es la cantidad de masa por unidad de volumen. Se denomina con la letra ρ. En el sistema internacional se mide en kilogramos / metro cúbico.
Peso específico de un líquido: El peso específico de un fluido se calcula como su peso sobre una unidad de volumen (o su densidad por g) . En el sistema internacional se mide en Newton / metro cúbico.
PREGUNTA: La hidrostática estudia:
Presión
PRESIÓN ATMOSFÉRICA
La atmósfera (capa de aire que rodea a la Tierra) ejerce, como cualquier otro fluido, una presión sobre los cuerpos que están en su interior.
Esta presión es debida a las fuerzas de atracción entre la masa de la tierra y la masa de aire y se denomina presión atmosférica.
La presión ejercida por la atmósfera se debe al peso de la misma (recordemos que peso p=masa*gravedad) y su valor es de 101.000 pascales, que corresponde a la presión normal.
existen otras unidades para emdir la presión y la equivalencia entre éstas son:
101.000 Pa(Pascales) = 1 atm(atmósfera) = 760 mmHg (milímetros de mercurio)
PRESIÓN HIDROSTÁTICA
Es la fuerza por unidad de área que ejerce un liquido en reposo sobre las paredes del recipiente que lo contiene y sobre cualquier cuerpo que se encuentre sumergido.
Supongamos que te sumerges en el mar, la presión que actúa sobre tu cuerpo depende del peso de la columna de agua que tengas encima, sobre la superficie de tu cuerpo. si te sumerges a un metro tendrás menos presión que si te sumerges a 2 metros o a 3.
La presión que ejerce un fluído sobre la paredes del recipiente o sobre la superficie de un cuerpo sumergido es siempre perpendicular a dicha superficie:
Donde:
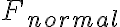 : Fuerza normal es aquella que es perpendicular a la superficie.
: Fuerza normal es aquella que es perpendicular a la superficie.
A es el área de la superficie.
Unidades de presión
Las unidades de presión son los  :
:
Pero existen varias utilizadas comúnmente:
PREGUNTA: La presión hidrostática, se define como:
VARIACIÓN DE LA PRESIÓN DENTRO DE UN FLUIDO
Así como la presión atmosférica disminuye con la altura, es de esperar que la presión en el interior de un líquido, aumente con la profundidad.
La presión es la misma en todos los puntos al mismo nivel de un fluido en reposo, observemos la figura:
El elemento de fluido marcado por lineas discontinuas está en equilibrio, sometido a fuerzas externas verticales, debidas a la presión en las secciones 1 y 2, y a su peso W , de manera que la condición de equilibrio, teniendo en cuenta convención de signos para escribir las ecuaciones de las fuerzas que actúan, es:
Realizaremos unas conversiones para determinar la presión a una profundidad dada:
En la lección 2 deciamos que la presión  y por tanto tenemos:
y por tanto tenemos:
 y
y 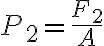 Si despejamos F de cada ecuación obtenemos:
Si despejamos F de cada ecuación obtenemos:
Ahora el peso de un cuerpo está dado por W=m*g (masa por gravedad).
La masa se puede definir como la densidad del cuerpo por el volumen.
y el volumen estará dado por el área del cuerpo por la altura:
Ahora remplazaremos en la ecuación original para obtener una ecuación en función de P, m,g y h.
Eliminamos A en cada uno de los miembros de la igualdad:
Entonces, considerando la segunda figura, la presión a una profundidad h , desde la superficie del fluido que está a la presión atmosférica, será:
Como la presión 1 es la presión que ejerce la atmósfera sobre el fluido podemos decir que la presión P a cualquier profundidad se determina por:
Donde:
P es la presión a una profundidad dada
g es el valor de la gravedad
h la profundidad a la que se encuentra la superficie del cuerpo
Ejemplo:
Un barril contiene una capa de aceite (D=600kg/m3) de 0,150m sobre 0,520m de agua. a) ¿Qué presión manométrica hay en la interfaz aceite-agua? b) ¿Qué presión manométrica hay en el fondo del barril?

a) Po=0
d aceite=600kg/m3
g=9.8m/s2
h aceite=0.150m
P=Patm + d*g*h; P=d*g*h
P=(600)(9.8)(0.150)
P=882Pa
b) Paceite + Pagua= P fondo del barril
882Pa + d agua*g*h agua= P fondo del barril
882Pa+ (1000)(9.8)(0.520)= P fondo del barril
P fondo del barril= 5.98 KPa
PREGUNTA: Un corto circuito deja sin electricidad a un submarino que está 50 m bajo la superficie del mar. Para escapar, la tripulación debe empujar hacia fuera una escotilla en el fondo que tiene un área 1 m2 y pesa 150 N. Si la presión interior es de 1 atm, ¿qué fuerza hacia abajo se debe ejercer sobre la escotilla para abrirla? Densidad del agua de mar=1030Kg/m2.
A) 100KN B) 504.7KN C) 504.7ATM D) 600KN
PRINCIPIO DE PASCAL
En las figuras se muestran dos situaciones: En la primera se empuja el líquido contenido en un recipiente mediante el émbolo de una jeringa, en la segunda, se empuja un bloque sólido. ¿Cuál es el efecto de estas acciones? ¿Qué diferencia un caso de otro?
La característica estructural de los fluidos hace que en ellos se transmitan presiones, a diferencia de lo que ocurre en los sólidos, que transmiten fuerzas. Este comportamiento fue descubierto por el físico francés Blaise Pascal (1623-1662), quien estableció el siguiente principio:
Un cambio de presión aplicado a un fluido en reposo dentro de un recipiente se transmite sin alteración a través de todo el fluido. Es igual en todas las direcciones y actúa mediante fuerzas perpendiculares a las paredes que lo contienen.
El principio de Pascal fundamenta el funcionamiento de las genéricamente llamadas máquinas hidráulicas: la prensa, el gato, el freno, el ascensor y la grúa, entre otras.
Cuando apretamos una chinche, la fuerza que el pulgar hace sobre la cabeza es igual a la que la punta de la chinche ejerce sobre la pared. La gran superficie de la cabeza alivia la presión sobre el pulgar; la punta afilada permite que la presión sobre la pared alcance para perforarla.
Cuando caminamos sobre un terreno blando debemos usar zapatos que cubran una mayor superficie de apoyo de tal manera que la presión sobre el piso sea la mas pequeña posible. Seria casi imposible para una mujer, inclusive las mas liviana, camina con tacones altos sobre la arena, porque se hundiría inexorablemente.
El peso de las estructuras como las casas y edificios se asientan sobre el terreno a través de zapatas de hormigón o cimientos para conseguir repartir todo el peso en la mayor cantidad de área para que de este modo la tierra pueda soportarlo, por ejemplo un terreno normal, la presión admisible es de 1,5 Kg/cm².
Observemos la siguiente figura:
El recipiente lleno de agua tiene dos pistones de diferente área. Si se ejerce una fuerza 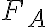 sobre el pistón pequeño de área
sobre el pistón pequeño de área 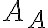 , la presión ejercida se transmite a todos los puntos del fluido dentro del recipiente y produce fuerzas perpendiculares a las paredes. Como los pistones pueden resbalar libremente en los cuellos donde están previstos, la porción de pared representada por el pistón B siente una fuerza
, la presión ejercida se transmite a todos los puntos del fluido dentro del recipiente y produce fuerzas perpendiculares a las paredes. Como los pistones pueden resbalar libremente en los cuellos donde están previstos, la porción de pared representada por el pistón B siente una fuerza  de manera que cuando el pistón
de manera que cuando el pistón 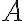 baja el pistón
baja el pistón 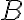 sube.
sube.
Como la presión interna es la misma en todos los puntos tenemos que:
Despejando obtenemos:
De donde se deduce que la fuerza se multiplica por la razón de las áreas de los pistones.
Ejemplo:
Una persona de 60 kg se encuentra de pie sobre la nieve. Si la superficie total de apoyo es de 250 cm2, a) ¿cuál es la presión que ejerce sobre la nieve? b) ¿Cuál sería la presión si estuviera provista de esquíes de 2 m de largo por 0,30 m de ancho? Expresa esta presión en atmósferas.
La presión es la fuerza dividida entre la superficie. P = F / A.
En este caso, la fuerza ejercida es el peso. Calculamos el peso: W = m*g W = 60kg * 9,8m/s2 = 588 N
La superficie de apoyo la expresamos en m2: A = 250 cm2· 1m2/ 10.000 cm2 = 0,025 m2
A continuación, calculamos la presión: P = 588N / 0,025 m2 = 23520 Pa
Calculamos la nueva superficie de apoyo. S = 2 m . 0,30 m = 0,6 m2
Con la nueva superficie, calculamos la nueva presión: P = 588 N / 0,6 m2 = 980 Pa
Para expresar este último valor en atm, debemos transformar de Pascal (N/m2) a atmósfera.
1 pascal = 9.869x10-6 Atmósfera.
1 atm. (kp/cm2) y 1 Pa (N/m2), entonces, 1 kp = 9,8N : 1m2 = 10000 cm2.
1 atm = 101325 Pa, entonces:
x = 1 atm * 980 Pa / 101325 Pa = 0.0096 atm.
PREGUNTA: Si añadimos un volumen de 100 cm3 de agua dentro de un tubo, ¿cuál será la presión hidrostática (debida al agua) en el punto donde se ha colocado la base (placa) del tubo?
Dato: A placa = 0,5 m2
D agua =1000kg/m3
Gravedad = 9,8 m/s2
a) 1960pa b) 196pa c) 1960kpa d) 1.96pa
PRINCIPIO DE ARQUÍMEDES: EMPUJE PRODUCIDO POR UN FLUIDO
Antes de entrar en materia recordemos algunos sucesos que nos han ocurrido en la vida diaria:
1. Cuando nos sumergimos en una piscina o en el mar parece que somos más ligeros, decimos que pesamos menos.
2. Los globos que se venden para niños se elevan en el aire al soltarlos.
3. Un trozo de hierro no flota, en general, sobre el agua, pero si le damos la forma adecuada, pensemos en un barco, vemos que flota.
La explicación científica sobre estos hechos la encontró en siglo IV a.C ARQUÍMEDES. Los fluidos ejercen fuerzas hacia arriba a los objetos que se encuentran sumergidos en ellos. La naturaleza y valor de estas fuerzas quedan determinadas en el Principio de Arquímedes:
"Todo cuerpo sumergido en un fluido (líquido o gas), experimenta una fuerza (empuje) vertical y hacia arriba igual al peso del fluido desalojado"
Empuje: De acuerdo con el principio fundamental de la hidrostática la presión en el interior de un líquido viene dada por la relación:
Además habíamos dicho que las fuerzas en el interior de los líquidos actúan perpendicularmente a las paredes del recipiente y a la superficie de los cuerpos dentro de dicho fluído.
Veamos la figura:
Las fuerzas laterales son iguales y se anulan: FL1 = FL2 , dado que la profundidad de ambas es la misma.
Las fuerzas verticales, las que actúan sobre la cara superior e inferior, no se anulan: F2 > F1, debido a que la cara inferior está a mayor profundidad.
La resultante de todas las fuerzas que actúan es una fuerza neta dirigida verticalmente hacia arriba, denominada fuerza de EMPUJE (E).
El valor del empuje viene dado por el Principio de Arquímedes:
¿Cómo saber si un cuerpo flotará o se hundirá?
Imaginemos que el cuerpo está totalmente sumergido, sobre el actúan dos fuerzas:
* El peso real del cuerpo fuera del líquido es P (peso real del cuerpo)= m*g.
Según sean los valores de E y P pueden darse tres casos:
1. Que el peso y el empuje sean iguales: E = Peso(m.g). El cuerpo estará en equilibrio (fuerza resultante nula) y "flotará entre aguas".
2. Que el empuje sea mayor que el peso: E > Peso(m.g) . El cuerpo ascenderá y quedará flotando.
3. Que el empuje sea menor que el peso : E < Peso (m.g). El cuerpo se hundirá.
¿A qué se llama peso aparente de un cuerpo?
Peso(aparente)=Peso (real)- Empuje |
Si un cuerpo flota, ¿qué volumen del cuerpo está sumergido? ¿y qué volumen emerge?
Si el empuje que calculamos suponiendo el cuerpo totalmente sumergido es mayor que el Peso real de dicho cuerpo, éste flotará.
El volumen de líquido desalojado no coincide con el volumen del cuerpo:
E = Peso (líq. desalojado) = m (líq. desalojado) . g = V (líq. desalojado). |
Si el cuerpo flota mantendrá una parte sumergida y otra emergida de tal forma que:
Peso real del cuerpo (m.g) = E (peso del líquido desalojado) |
Ejemplo:
Imagina que pesas con el dinamómetro un objeto cuyo valor es de 1 newton en el aire y al introducirlo en el agua totalmente pesaba 0,8 newton. Calcula el volumen del objeto y su densidad. Densidad del agua = l.000 kg/m3
Solución:
El empuje producido por el agua es: E = 1N - 0,8N = 0,2 N.
E = V.d.g tenemos que: 0,20 = V * 1.000kg/m3 * 9,8 m/s2 V= 0,20N / 9800kg*m/m3 *s2
V = 2,04 * l0-5 m3 = 20,4 cm3
Este volumen del líquido desalojado coincide exactamente con el volumen de la piedra.
Ahora calcularemos la masa de la misma y su densidad:
m = P / g = 1 newton / 9,8 m/s2 = 0,102 kg = 102 g
d = m/V = 0,102 kg / 2,04 * l0-5 m3 = 5 . l03 kg/m3
PREGUNTA: Un cuerpo cuyo volumen es de 0,08 dm3 y que pesa en el aire 12 N se introduce en mercurio. Si, mediante un dinamómetro, medimos el peso del cuerpo dentro del mercurio (13600 kg/m3), ¿qué valor hallaremos?
a) 1.26624
KN b) 10.6624N c) 1,3376 N d) 10.66 KN
Medición de la presión
Manómetro
Es un elemento de medición, en forma de U, que sirve para medir la presión de los fluidos contenidos en recipientes cerrados.
Muchos de los aparatos empleados para la medida de presiones utilizan la presión atmosférica como nivel de referencia y miden la diferencia entre la presión real o absoluta y la presión atmosférica, llamándose a este valor presión manométrica.
Una de las ramas del tubo está abierta a la atmósfera y la otra está conectada con el depósito que contiene el fluido cuya presión se desea medir:
El fluído del recipiente penetra en parte del tubo en U, haciendo contacto con la columna líquida. Los fluídos alcanzan una configuración de equilibrio de la que resulta fácil deducir la presión manométrica en el depósito:

Donde:
p es la presión real
 es la densidad de líquido manométrico (mercurio, agua, aceite...)
es la densidad de líquido manométrico (mercurio, agua, aceite...)
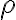 Densidad del fluído contenido en el depósito.
Densidad del fluído contenido en el depósito.
Barómetro
Un barómetro es aquel instrumento utilizado para medir la presión atmosférica, construido por TORRICELLI.
El barómetro de mercurio está hecho de un tubo de 1 m de altura, que en su interior cuenta con mercurio. Este tubo, fabricado en vidrio, en su extremo superior se encuentra cerrado, mientras que en el inferior está abierto. El tubo es llenado de mercurio y se invierte para luego ser colocado dentro de una cubeta, también llena de mercurio.
Luego, el mercurio del tubo desciende hasta lograr una altura de 760 mm aproximadamente, por sobre el nivel de la cubeta, a la que se le denomina altura barométrica. Lo anterior, permite que se produzca un vacío en el extremo superior del tubo. A este vacío se le llama cámara barométrica. Finalmente, la presión atmosférica estará dada por las variaciones de altura del mercurio luego del proceso anterior. Esta variación fluctúa entre los 737 y los 775 mm de altura.
¿Por qué el mercurio no descendió más? El tubo no se vació porque el aire exterior presionaba sobre el mercurio de la cubeta (en cambio, en la parte superior del tubo se produjo vacío). La presión ejercida por la atmósfera en el punto P es igual a la presión en Q, ya que ambos puntos están al mismo nivel en el mismo fluido. Es decir que la presión que la columna de aire de casi 40 km de altura (la atmósfera) ejerce sobre la superficie libre del mercurio (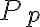 ) es igual a la que ejerce la columna de 76 cm de mercurio, entonces:
) es igual a la que ejerce la columna de 76 cm de mercurio, entonces:
Patm= PHg hHg = 13,6 g/cm3 . 76cm = 1.033,6 g/cm2 = 101.293 N/m2 = 101.293 Pa
Este valor, que corresponde a la presión atmosférica normal, se llama atmósfera (atm). También se acostumbra a dar la presión atmosférica en milímetros de mercurio (Torr) o en milibares (1mb = 0,75 Torr).
1 atm = 760 mm Hg = 760 Torr
También se usa el bar como unidad y su valor es: 1 bar = 105 nt/m2 =105 Pa.
PREGUNTA: ¿Cuál es el instrumento utilizado para medir la presión atmosférica?
Hidrodinámica y ecuación de continuidad
HIDRODINÁMICA
La hidrodinámica es el estudio de los fluidos en movimiento. Admitiremos que el fluido no es viscoso, es decir que no hay rozamiento entre las capas de fluidos que pueden dar lugar a pérdida de energía mecánica.
Nuestro estudio de hidrodinámica se limita solamente a los fluidos incompresibles (densidad constante), no viscosos.
Veamos algunos conceptos necesarios para entrar en materia:
CAUDAL
Es la cantidad de líquido que pasa por una sección en determinado tiempo.
Caudal volumétrico: Es el volumen de líquido que atraviesa una sección dividido en el tiempo que tarda en pasar.
Donde
Q es el caudal
V el volumen de líquido
t el tiempo
Las unidades del caudal son:  ;
;  .
.
Caudal másico: Masa de líquido que atraviesa una sección en la unidad de tiempo.
Se puede realizar conversión de caudal másico a caudal volumétrico teniendo en cuenta la relación:
Donde
V es el volumen de líquido
m es la masa
El caudal también podemos hallarlo teniendo en cuenta la velocidad del líquido dentro de la sección:
Si observamos la gráfica vemos como el líquido al moverse dentro de la sección o tubo recorre una distancia d. El volumen de líquido que circula puedo expresarlo como 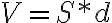 , donce V es el volumen, S es la superficie o área del tubo y d la distancia que recorre.
, donce V es el volumen, S es la superficie o área del tubo y d la distancia que recorre.
 recordemos que distancia/tiempo es velocidad:
recordemos que distancia/tiempo es velocidad:
Donde
S es la superficie o área de la sección por donde pasa el líquido
v es la velocidad con la cual pasa por esa sección
Importante no confundamos V con 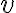 , mayúscula se utiliza para el volumen y minúscula para la velocidad.
, mayúscula se utiliza para el volumen y minúscula para la velocidad.
ECUACIÓN DE CONTINUIDAD
Antes de hablar de la ecuación de continuidad pensemos el siguiente razonamiento:
Por una tubería de 10 cm ingresan 5 litros de agua por minuto. ¿Qué cantidad de agua sale por el otro extremo del tubo?
La respuesta es la que estás pensando. Todo lo que ingresa al tubo debe salir por el otro extremo. Y éste es el principio básico para formular la ecuación de continuidad.
Por la definición de caudal  se tiene que:
se tiene que:
Observando la gráfica podemos obtener que la ecuación de continuidad es:
Donde
S son las superficies o áreas en cada extremo del tubo
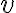 las velocidades en cada extremo del tubo
las velocidades en cada extremo del tubo
Esta ecuación llamada de continuidad es la expresión matemática de la conservación de la masa total del fluído, de la cual podemos concluir que si la sección de un tubo de flujo se estrecha, la velocidad del fluido aumenta, y de ésta manera se conserva el caudal en el mismo.
PREGUNTA: La hidrodinámica es el estudio de los fluidos en movimiento?:
Teorema de Bernoulli y Teorema de Torricelli
Esta ecuación es la conservación de la energía para el líquido que va dentro de un tubo. No se puede plantear si el líquido tiene viscosidad. Así como los sólidos existe el rozamiento, en los líquidos se denomina viscosidad.
Donde
Simbología | Significado | Unidades |
Presión de entrada | ||
Presión de salida | ||
Densidad de líquido | ||
Velocidad de entrada | ||
Velocidad de salida | ||
Aceleración de la gravedad | ||
Altura del líquido a la entrada del tubo o sistema | ||
Altura del líquido a la salida del tubo o sistema |
Para tubos verticales se debe tener en cuenta por cuál extremo ingresa el fluído, ya que es un factor primordial a la hora de plantear las alturas de cada extremo.
Cuando el tubo cambia de diámetro de la sección de en medio se debe plantear cada cambio de sección por separado, es decir, que variable se tiene en cada sección en donde el cambio de diámetro se evidencia:
En caso de tubo inclinado tenemos diferentes valores para h.
Ejemplo:
Un tubo que conduce un fluido incomprensible cuya densidad es 1,30 x 103 kg/m3, es horizontal en h0 = 0 m. Para evitar un obdtáculo, el tubo se debe doblar hacia arriba, hasta alcanzar una altura de h1 = 1 m. El tubo tiene área transversal constante. Si la presión en la sección inferior es P0 =1,50 atm, calcule la presión P1 en la parte superior.
Solución:
Al tener área transversal constante, no debe cambiar la velocidad del fluido en su interior, por lo tanto: v0 = v1 = v
Entonces, aplicando la ecuación de Bernoulli, se tiene:
P0 + ρgh0 + ½ ρv2 = P1 + ρgh1 + ½ ρv2
P0 + ρgh0 = P1 + ρgh1 De donde: P1 = P0 + ρgh0 - ρgh1
Como P0=1,50 atm; 1atm = 101325Pa, entonces debemos convertir atmosfera a pascal
P1 = 151987,5 Pa + (1,30 x 103 kg/m3)(9,8m/s2)(0m) - (1,30 x 103 kg/m3)(9,8m/s2)(1m)
P1 = 151987,5 Pa – 12740 Pa
P1 = 139247,5 Pa = 1,37 atm
PREGUNTA: Un fluido fluye de izquierda a derecha por un tubo cilindrico. La densidad de la sustancia es 1,5 kg/m3. Su velocidad en el extremo de entrada es v0 = 2 m/s, y la presión allí es de 1,5 Pa y el radio de la sección es r0 = 10 cm. El extremo de salida está a 4,5 m abajo del extremo de entrada y el radio de la sección allí es r1 = 8 cm. Encontrar la presión P1 en este extremo del tubo?. Nota: para este ejercicio se utiliza la ecuación de continuidad, S1 v1 = S0 v0, donde S= πr2.
a) -68,97 Pa. b) -6,8
Pa. c) -6,97 Pa. d) 68,97 Pa
ANÁLISIS DE LAS ECUACIONES DE CONTINUIDAD Y BERNOULLI
En hidrodinámica tenemos dos ecuaciones fundamentales para resolver los ejercicios: El teorema de Bernoulli y la ecuación de continuidad.
 Ya que el caudal de entrada es el mismo que el caudal de salida.
Ya que el caudal de entrada es el mismo que el caudal de salida.
 Por que se cumple que éste valor de la igualdad debe ser igual en ambos miembros.
Por que se cumple que éste valor de la igualdad debe ser igual en ambos miembros.
CONCEPTO UNO: A MAYOR SECCIÓN, MENOR VELOCIDAD
De la ecuación de continuidad se puede hacer una deducción importante: Si el valor  siempre se tiene que mantener constante, entonces donde el tubo sea más angosto LA VELOCIDAD SERÁ MAYOR.
siempre se tiene que mantener constante, entonces donde el tubo sea más angosto LA VELOCIDAD SERÁ MAYOR.
Esto pasa porque el caudal que circula es constante. Entonces si el tubo se hace más angosto, para que pueda circular el mismo caudal, la velocidad de líquido tiene que aumentar.
Exactamente lo contrario pasa si el caño se hace más ancho,la velocidad del líquido tiene que disminuir para que pueda seguir pasando el mismo caudal.
CONCEPTO DOS: A MAYOR VELOCIDAD, MENOR PRESIÓN
Algo importante que se puede deducir de la ecuación de Bernoulli es que en el lugar donde la velocidad del líquido que circula sea mayor, la presión será menor.
Aclaración importante: Esto pasa solo si el tubo es horizontal.
En realidad el término  vale lo mismo que el término
vale lo mismo que el término 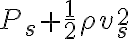 . Es decir, si al lado izquierdo de la ecuación vale 5, el lado derecho también tiene que valer 5.
. Es decir, si al lado izquierdo de la ecuación vale 5, el lado derecho también tiene que valer 5.
Supongamos que estás lavando el carro con una manguera y aprietas la punta. El diámetro de la manguera se achica y ahora el agua sale con mayor velocidad.
Como la velocidad de salida aumenta, la presión de salida tendrá que disminuir para mantener la igualdad de los términos a la derecha y a la izquierda de la ecuación.
Es decir que si la velocidad a la salida aumenta, la presión a la salida va a disminuir.
CONCEPTO TRES: A MAYOR SECCION, MAYOR PRESION
Hasta ahora relacionamos el concepto de sección con el de velocidad y el concepto de velocidad con el de presión. Ahora vamos a relacionar el concepto de sección con el de presión.
Por un lado dijimos que a menor sección, mayor velocidad (Continuidad).
Por otro lado te dije que a mayor velocidad, menor presión. (Bernoulli en tubos horizontales).
Uniendo estas 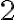 ideas en una sola, podemos decir que a menor sección, menor presión. O lo que es lo mismo, a mayor sección, mayor presión.
ideas en una sola, podemos decir que a menor sección, menor presión. O lo que es lo mismo, a mayor sección, mayor presión.
Esta conclusión significa que donde mayor sea el diámetro del tubo, mayor va a ser la presión en el líquido que circula. Esto es válido sólo para tubos horizontales.
PREGUNTA: ¿Cómo se comportan la presión y la sección, si la velocidad aumenta?
La presión
aumentada y la sección disminuida.
La presión y
la sección estarían disminuidas
La presión
disminuida y la sección aumentada.
La presión y
la sección estarían aumentadas
Ejercicios aplicativos de Teorema de Bernoulli, Torricelli y ecuación de continuidad
EJERCICIOS APLICATIVOS
Ejercicio 1: Por un tubo ubicado en forma horizontal circula agua con un caudal de  . Inicialmente la superficie del tubo es
. Inicialmente la superficie del tubo es  y la sección va disminuyendo hasta alcanzar un área de 1m^2.
y la sección va disminuyendo hasta alcanzar un área de 1m^2.
a) Cuál es la velocidad del agua al ingresar al tubo.
b) Cuál es la diferencia de presión entre las dos secciones.
c) En qué sección del tubo es mayor la presión.
Inicialmente debemos elaborar un dibujo que nos permita identificar qué nos plantea el problema.
b) Ahora hallaremos la velocidad de salida, necesaria para encontrar la diferencia de presiones:
Nota: Una diferencia, como ya sabemos es una resta, por tanto cuando me piden diferencia de presiones, solicitan que halle 
Como el tubo está en posición horizontal 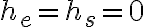
c) La presión a la entrada es mayor que a la salida porque a la entrada la velocidad es menor (La sección a la entrada es mas grande ), y como la velocidad es menor, la presión será mayor. Para deducir esto apliqué el principio de mayor velocidad, menor presión de la lección 9.
Ejercicio 2: Un líquido de densidad 1,2 g/cm3 ó 1,2 X 103 kg/m3 fluye como muestra la figura:
Calcular:
(a) La velocidad de salida del líquido.
(b) La cantidad de líquido que sale por segundo
(c) La velocidad del líquido en la sección 3.
(d) La presión en la sección 3.
(e) La diferencia de altura entre las columnas de mercurio del tubo en U.
Solución:
a) Velocidad de salida del líquido: Planteemos la ecuación de Bernoulli entre las secciones (1) y (2):
Se tiene que el término  en la sección 2 es 0 porque la altura h en tubos horizontales es 0.
en la sección 2 es 0 porque la altura h en tubos horizontales es 0.
Ahora tenemos que 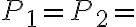 presión atmosférica,
presión atmosférica,  ya que inicialmente está en reposo y empieza a salir a una velocidad mínima que odemos tomarla como despreciable y la densidad
ya que inicialmente está en reposo y empieza a salir a una velocidad mínima que odemos tomarla como despreciable y la densidad  es la misma, entonces podemos eliminarlos de la ecuación:
es la misma, entonces podemos eliminarlos de la ecuación:
b) La cantidad de líquido que sale por segundo es
La superficie o área de un círculo (forma de la boca del tubo) es  , y el diámetro del tubo en la sección 2, que es el de salida es 8 cm r=D/2 por tanto r=4 cm=0.04 m:
, y el diámetro del tubo en la sección 2, que es el de salida es 8 cm r=D/2 por tanto r=4 cm=0.04 m:
c) Velocidad del líquido en la sección 3: Por la ecuación de continuidad, tenemos:
d)La presión en la sección 3: Planteemos la ecuación de Bernoulli entre las secciones (2) y (3):
Organizando términos y factorizando términos semejantes obtenemos:
Como realizamos la diferencia de presiones tenemos la presión manométrica. Como nos piden la presión en 3 (presión absoluta), recordemos que  .
.
Cada uno de los estudiantes deben calcular ésta presión en 3.
e) Diferencia de altura entre las columnas de mercurio:
Observando la gráfica podemos deducir que 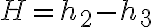
Las secciones que afectan la entrada y salida del tubo de mercurio (Hg) son 3) y 2). Recordando que los términos en ambos lados de la igualdad en la ecuación de bernoulli deben ser constantes (lección 9) tenemos:
El valor 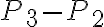 lo hallamos en el punto anterior, y el valor de la gravedad se toma negativo y lo aproximamos a
lo hallamos en el punto anterior, y el valor de la gravedad se toma negativo y lo aproximamos a  :
:
PREGUNTA: Por una cañería circula agua con un régimen estacionario a caudal constante. Considerando dos secciones de esa cañería; S1 =  y S2 =
y S2 =  , ¿cuál será la velocidad en la segunda sección, si en la primera es de 8 m/s?
, ¿cuál será la velocidad en la segunda sección, si en la primera es de 8 m/s?
a) 20
m/s b) 2 m/s c) 40 m/s
d) 3.2 m/s




























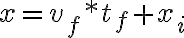


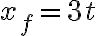
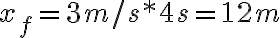




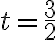



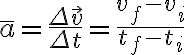






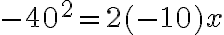

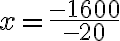





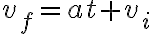
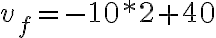
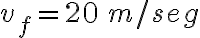


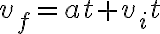








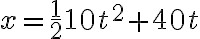







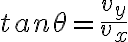









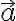




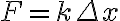


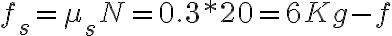

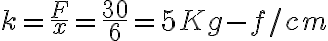








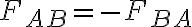
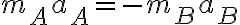









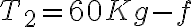

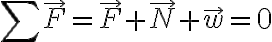




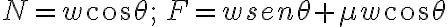






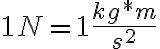










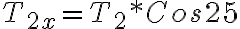
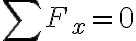
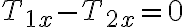






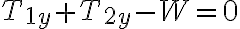
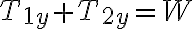



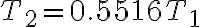


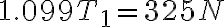
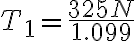





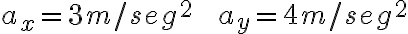







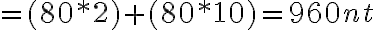





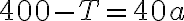












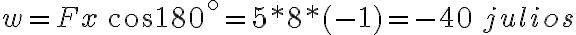






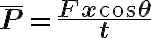










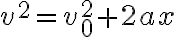


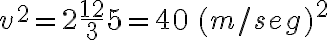

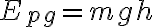
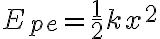
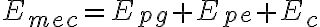



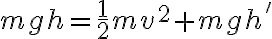







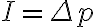











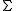



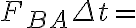

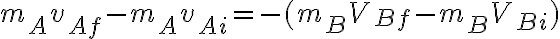


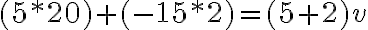
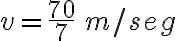







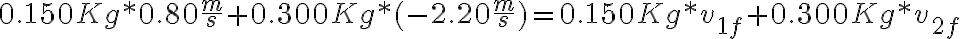

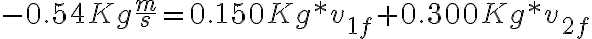

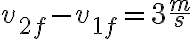
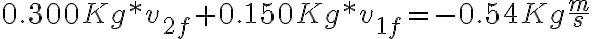
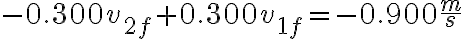
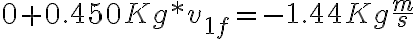

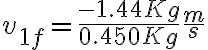








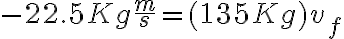





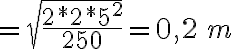





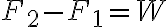

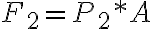













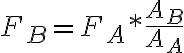






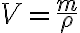









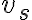


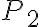







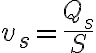
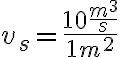

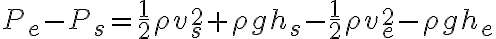



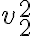
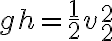



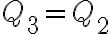




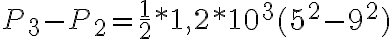


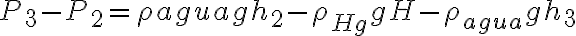

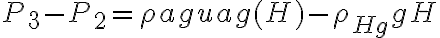

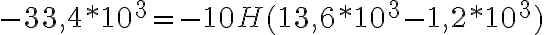

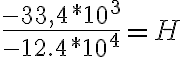



Comentarios
Publicar un comentario